css的2D转换

脚本化css
下面通过css实现动画效果，可以使用脚本化的css实现滑入，轮廓伸缩的列表，即动态的HTML，一个过时的说法DHTML

一些css的基础知识

之前已经看过厚厚的一本大书，现在简单看一下，补充一下不知道的点

层叠

web浏览器组合元素的style属性，然后再计算样式。

颜色透明度和半透明

颜色有半透明的颜色（不知道为什么edge不兼容）

脚本化内联样式

div.style.background = "#FFFFFF"

即通过js完成css样式的添加

由于-会被js认为有语法错误，所以-统一在js中变成驼峰命名法进行命名。这是一种习惯

同样的也可以直接使用属性进行设置

e.setAttribute

进行设置css的内联样式

其实是通过增加css的属性的内联样式达到效果的。即style的值

style的权重要大于任何的样式，所以用js生成的style的样式的值，一直起作用，除非刻意的更改其权重。

css的2d转换

即，进行一些css的转换

坐标

描述坐标的系统有笛卡尔坐标系统和齐次坐标系。

笛卡尔坐标系

用一组数值在一组平面上表示一个点。其坐标为右手法则（在三维上）
更多 https://en.wikipedia.org/wiki/Cartesian_coordinate_system
其下方的变换是基于笛卡尔坐标系进行变换
通过将点用矩阵进行表示，对矩阵进行变换，（线性的变换）得到相应的结果。例如进行乘法变换，加法变换等等。

transform

属性将会允许修改CSS视觉格式模型的坐标空间。使用它，元素可以被转换（translate）、旋转（rotate）、缩放（scale）、倾斜（skew）。 只对块级元素生效

原点

有三个值，一个值为x轴，一个值为y轴，一个值为z轴。
如下图所示

每个值可以进行设置，此为旋转原点
具体的值为transform-origin
如果未指定初始值，将会直接使用继承。

演示

https://developer.mozilla.org/zh-CN/docs/Web/CSS/transform-origin

rotate旋转

该方法定义了一种将元素围绕一个定点，该定点由transform-origin指定元素变形的原点。

单位 angle

一种css的基本数据类型。angle表示角的大小，单位为度（degrees）百分度（gradians）弧度（radians）圈数（turns）
deg 度
grad 百分度 （复习一下数学，一种角的测量单位，定义为将一个圆切成400等分，也就是一个直角等于100百分度 https://zh.wikipedia.org/wiki/百分度）
rad 弧度 （复习一下数学 https://zh.wikipedia.org/wiki/弧度）
turn 圈数

不列颠百科全书 https://www.britannica.com/biography/August-Ferdinand-Mobius

语法

数字与单位之间没有空格。数字为0时，单位可以省略。
使用+号或者-号开头，正数表示顺时针的角，负数表示逆时针的角。

一些例子

90deg = 100grad = 0.25trun ≈ 1.57rad(约等于π/2)
所有的如下表示

一个旋转说明

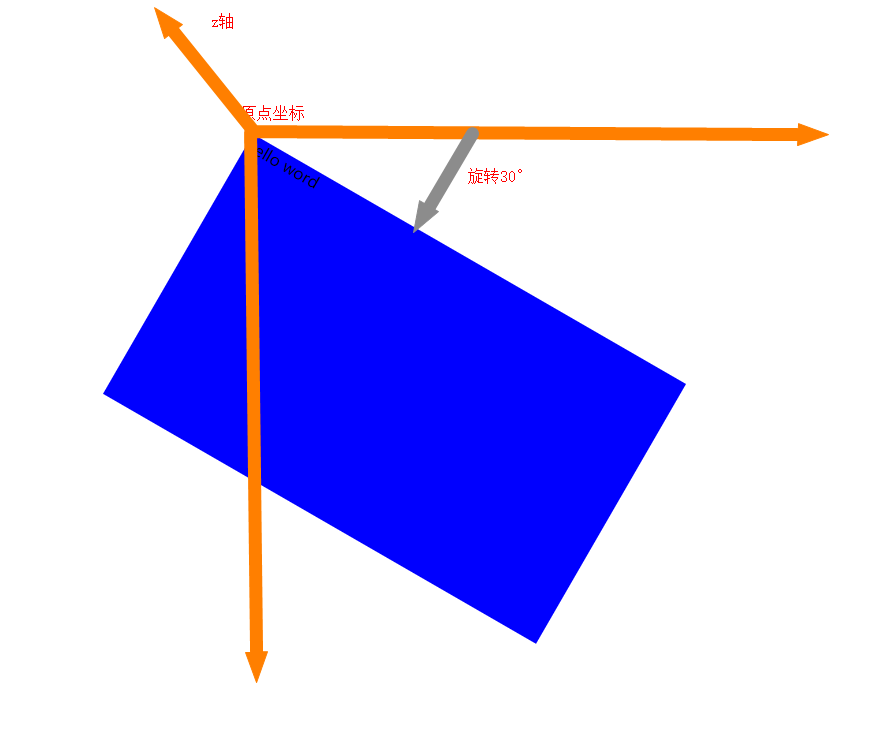
缩放 scale

一个css函数scale()用于缩放。用于修改元素的大小，通过向量形式定义的缩放值来放大和缩小元素。有两个值，一个值为sx，一个值为sy，根据两个值得出结果。如果sy未设置，将会直接用sx的值设置sy的值。其单位为css数据类型中的number

该缩放仅仅支持欧几里得平面（二维平面）上的变换

设置的css的值为

transform: scale(2, 2);

至此，完成了一个横轴一倍，纵轴一倍的放大。
同理，缩小也可以。

倾斜 skew

为一个偏斜的二维平面上的原件变化，其结果为数据类型。

剪切映射

css的倾斜为剪切映射,每个点的坐标由与指定角度或成比例的值到原点的距离。对于每个坐标产生矩阵，然后对矩阵进行运算，得出运算后的坐标值。

css的3d转换

坐标

齐次坐标系

由笛卡尔坐标系投影得到。

1. 投影平面中的任何点由三元组（x，y，z）表示，称为点的齐次坐标和投影坐标
2. 如果坐标乘以公因子，则给定的一组齐次坐标点不变
3. 相反，当且仅当通过所有坐标乘以相同的非零常数，从另一个获得一个时，两组齐次坐标表示相同的点
4. 当z不为0时，表示的点为欧几里得的点。
5. 当z为0时表示的点为无穷远处的点
   更多 https://en.wikipedia.org/wiki/Homogeneous_coordinates

rotateX()

围绕x轴进行旋转

ps；设置的原点值为center
即

transform-origin:center;

rotateY()同理

3d组合不可进行交换，如果进行交换会导致出现不同的效果。