数据结构入门-树的遍历以及二叉树的创建

zoukankan html css js c++ java

数据结构入门-树的遍历以及二叉树的创建
树定义：
1. 有且只有一个称为根的节点
2. 有若干个互不相交的子树，这些子树本身也是一个树
通俗的讲：
1. 树是有结点和边组成，
2. 每个结点只有一个父结点，但可以有多个子节点
3. 但有一个节点例外，该节点没有父结点，称为根节点
一、专业术语

结点、父结点、子结点、根结点

深度：从根节点到最底层结点的层数称为深度，根节点第一层

叶子结点：没有子结点的结点

非终端节点：实际上是非叶子结点

度：子结点的个数成为度

二、树的分类

一般树：任意一个结点的子结点的个数都不受限制

二叉树：任意一个结点的子结点个数最多是两个，且子结点的位置不可更改

二叉数分类：
1. 一般二叉数
2. 满二叉树：在不增加树层数的前提下，无法再多添加一个结点的二叉树
3. 完全二叉树：如果只是删除了满二叉树最底层最右边的连续若干个结点，这样形成的二叉树就是完全二叉树
森林：n个互不相交的树的集合

三、树的存储

二叉树存储

连续存储(完全二叉树)

优点：查找某个结点的父结点和子结点(也包括判断有没有子结点)速度很快

缺点：耗用内存空间过大

链式存储

一般树存储
1. 双亲表示法：求父结点方便
2. 孩子表示法：求子结点方便
3. 双亲孩子表示法：求父结点和子结点都很方便
4. 二叉树表示法：把一个一般树转化成一个二叉树来存储，
  
  具体转换方法：
  
  设法保证任意一个结点的左指针域指向它的第一个孩子，右指针域指向它的兄弟，只要能满足此条件，就可以把一个一般树转化为二叉树
  
  一个普通树转换成的二叉树一定没有右子树
森林的存储

先把森林转化为二叉树，再存储二叉树

四、树的遍历

先序遍历：根左右

先访问根结点，再先序访问左子树，再先序访问右子树

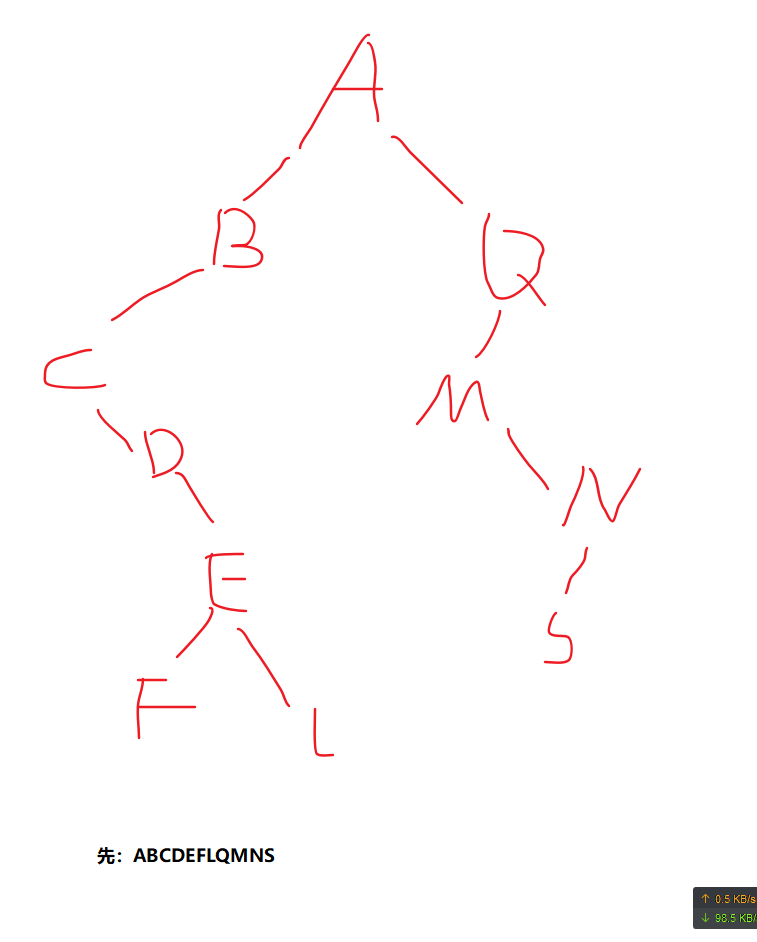
中序遍历：左根右

中序遍历左子树，再访问根结点，再中序遍历右子树

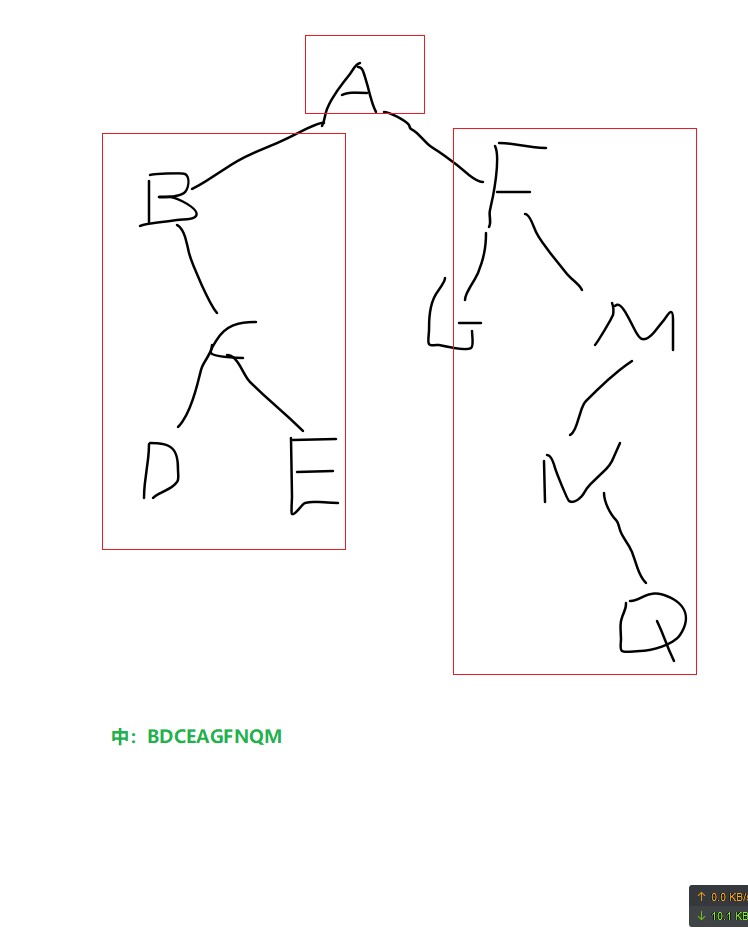
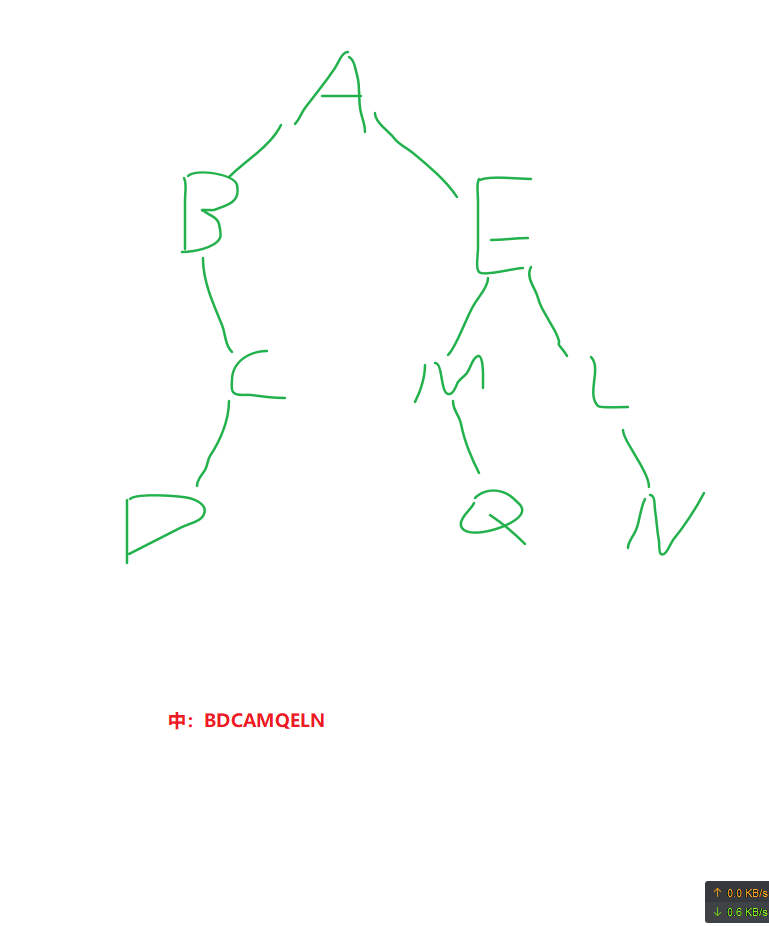
后续遍历：左右根

后续遍历左子树，后续遍历右子树，再访问根节点

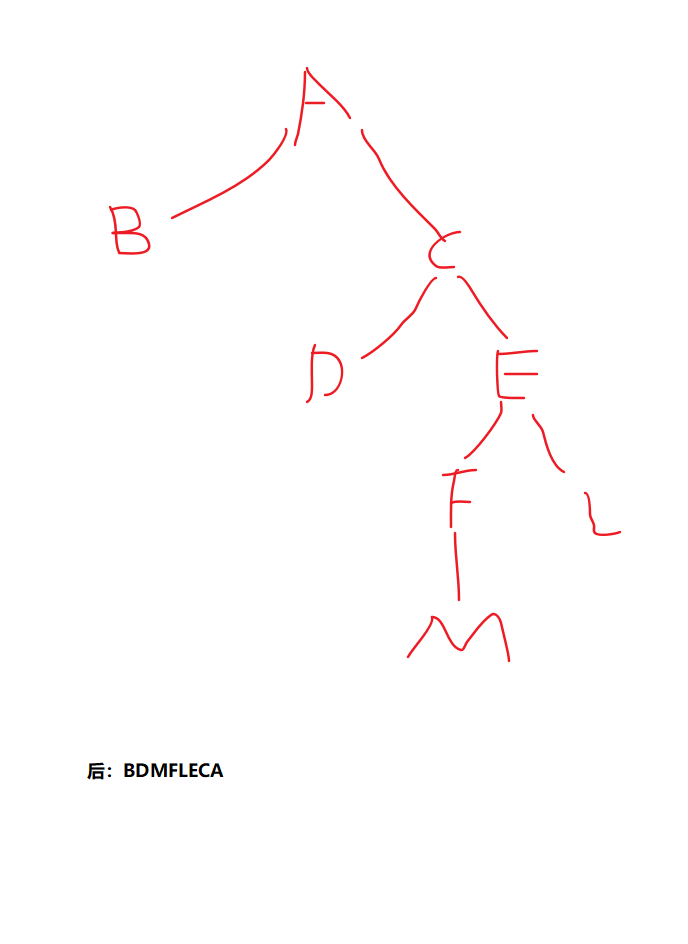
五、已知两种遍历求原始二叉树

给定了二叉树的任何一种遍历序列，都无法唯一确定相应的二叉树，但是如果知道了二叉树的中序遍历序列和任意的另一种遍历序列，就可以唯一地确定二叉树

已知先序和中序求后序

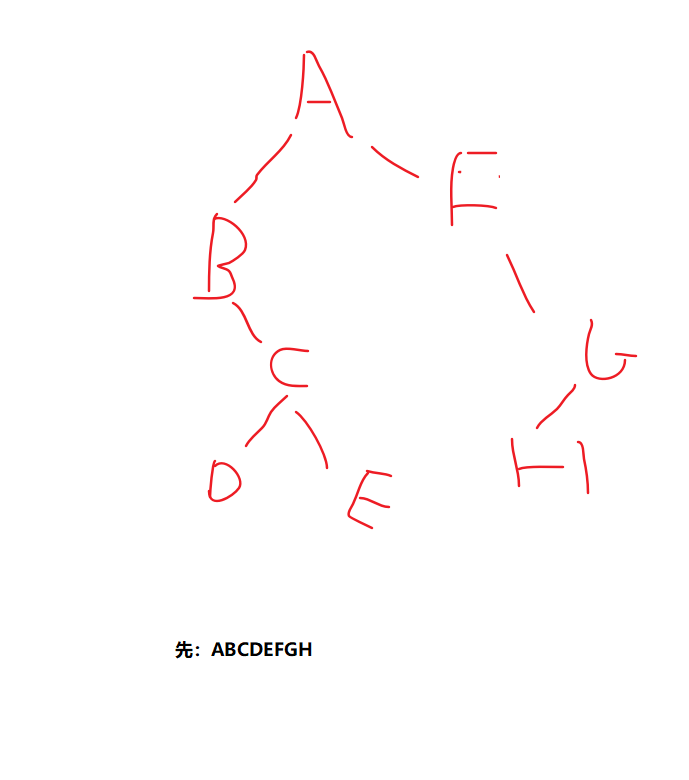
先序：ABCDEFGH

中序：BDCEAFHG

求后序：这个自己画个图体会一下就可以了，非常简单，这里简单记录一下
1. 首先根据先序确定根，上面的A就是根
2. 中序确定左右，A左边就是左树(BDCE)，A右边就是右树(FHG)
3. 再根据先序，A左下面就是B，然后根据中序，B左边没有，右边是DCE
4. 再根据先序，B右下是C，根据中序，c左下边是D，右下边是E，所以整个左树就确定了
5. 右树，根据先序，A右下是F，然后根据中序，F的左下没有，右下是HG，
6. 根据先序，F右下为G，然后根据中序，H在G的左边，所以G的左下边是H
再来一个例子，和上面的思路是一样的，这里就不详细的写了

先序：ABDGHCEFI

中序：GDHBAECIF

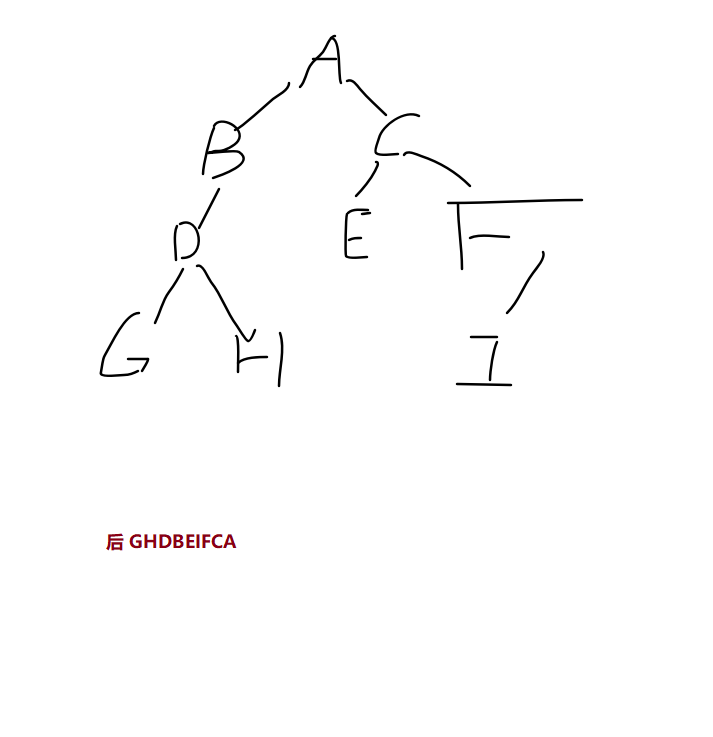
已知中序和后序求先序

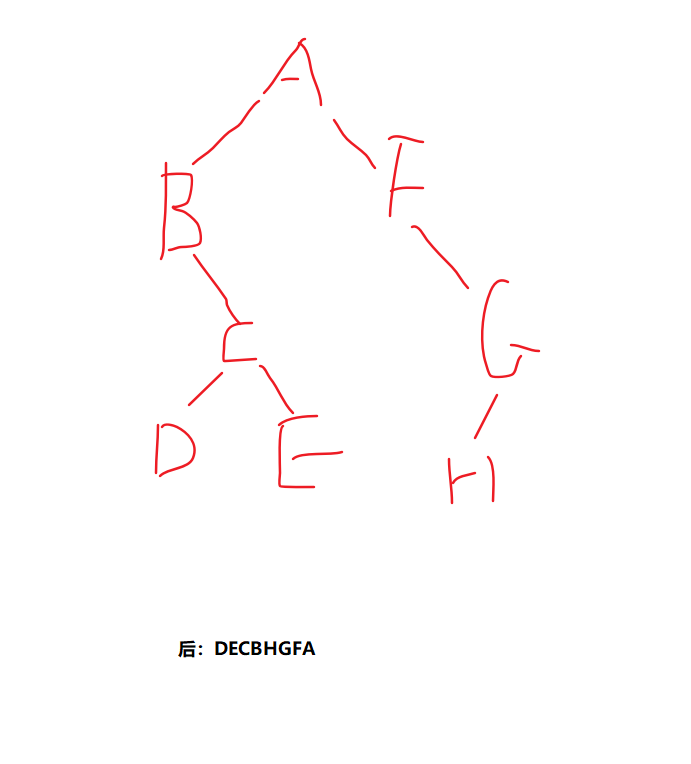
中序：BDCEAFHG

后序：DECBHGFA

这个和上面的思路是一样的，只不过是反过来找，后序找根，中序找左右

树简单应用

树是数据库中数据组织一种重要形式

操作系统子父进程的关系本身就是一棵树

面向对象语言中类的继承关系

哈夫曼树

六、二叉树的创建
```
#include <stdio.h>
#include <stdlib.h>

typedef struct Node
{
	char data;
	struct Node * lchild;
	struct Node * rchild;
}BTNode;

/*
二叉树建立
*/
void BuildBT(BTNode ** tree)
{
	char ch;
	scanf("%c" , &ch); // 输入数据
	if(ch == '#')  // 如果这个节点的数据是#说明这个结点为空
		*tree = NULL;
	else
	{
		*tree = (BTNode*)malloc(sizeof(BTNode));//申请一个结点的内存
		(*tree)->data = ch; // 将数据写入到结点里面
		BuildBT(&(*tree)->lchild); // 递归建立左子树
		BuildBT(&(*tree)->rchild); // 递归建立右子树
	}
}

/*
二叉树销毁
*/
void DestroyBT(BTNode *tree) // 传入根结点
{
	if(tree != NULL)
	{
		DestroyBT(tree->lchild);
		DestroyBT(tree->rchild);
		free(tree);  // 释放内存空间
	}
}

/*
二叉树的先序遍历
*/
void Preorder(BTNode * node)
{
	if(node == NULL)
		return;
	else
	{
		printf("%c ",node->data );
		Preorder(node->lchild);
		Preorder(node->rchild);
	}
}

/*
二叉树的中序遍历
*/
void Inorder(BTNode * node)
{
	if(node == NULL)
		return;
	else
	{
		
		Inorder(node->lchild);
		printf("%c ",node->data );
		Inorder(node->rchild);
	}
}


/*
二叉树的后序遍历
*/
void Postorder(BTNode * node)
{
	if(node == NULL)
		return;
	else
	{
		
		Postorder(node->lchild);
		Postorder(node->rchild);
		printf("%c ",node->data );
	}
}

/*
二叉树的高度
树的高度 = max(左子树高度，右子树高度) +1
*/
int getHeight(BTNode *node)
{
	int Height = 0;
	if (node == NULL)
		return 0;
	else
	{
		int L_height = getHeight(node->lchild);
		int R_height = getHeight(node->rchild);
		Height = L_height >= R_height ? L_height +1 : R_height +1;
	}

	return Height;
}


int main(int argc, char const *argv[])
{
	BTNode * BTree; // 定义一个二叉树
	printf("请输入一颗二叉树先序序列以#表示空结点:");
	BuildBT(&BTree);

	printf("先序序列：");
	Preorder(BTree);
	printf("
中序序列：");
	Inorder(BTree);
	printf("
后序序列：");
	Postorder(BTree);

	printf("
树的高度为：%d" , getHeight(BTree));
	return 0;
}
// ABC##DE##F##G##
```
查看全文