机器学习与数据分析课程笔记-分类-logistic回归

logistic回归虽然被称为回归但是其实它时常用于分类。

什么是分类?

常见的分类以下例子:

• 判断肿瘤良性恶性
• 判断在线交易是否是伪交易
• 判断明天是否下雨

回答都是（Yes或者No），相当于将数据分为两类。分别用0和1代表，0代表负类，1代表正类

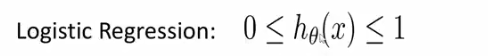
逻辑回归主要解决二分类问题，逻辑回归在线性回归的基础上进行了变换。logistic回归在线性回归的基础上，进一步变换，使得模型假设的取值范
围在[0，1]

逻辑回归如何进行分类？

逻辑回归的输出是一个[0,1]之间的数，如果那个数靠近0，那么我们就认为其属于负例，如果靠近1，那么就认为它属于正例。

逻辑回归如何将线性回归的值放到[0,1]之间的呢？

找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来

如何找这样的函数呢？

1.单位阶跃函数

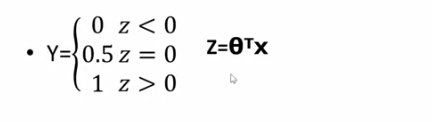
这样变换，得到的输出值，仅能取[0,0.5,1]三个数。所以该函数不连续，求导比较麻烦。

2.对数几率函数

该函数可以将一个任意大小的输入变换到[0,1]之间的输出。

注意：当x->正无穷或者x->负无穷的时候，该函数输出无限接近1或者0，而非等于1或者0.

该函数的求导:

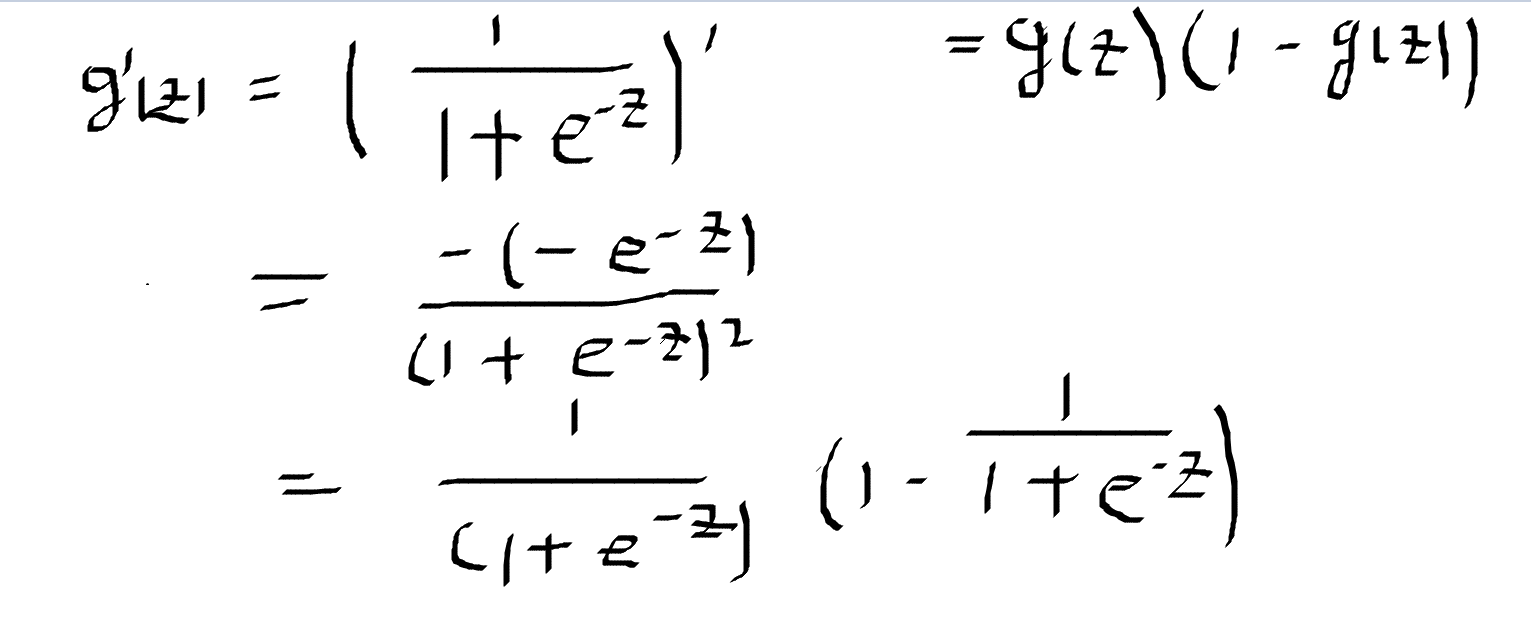
逻辑回归在线性变换的基础上，用对数几率函数变换一下，得到输出。进而y在[0,1]之间，z是线性变换得到的结果，将z代入g得到[0,1]之间的数:

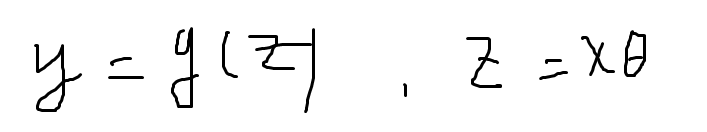
对于y进行变换一下:

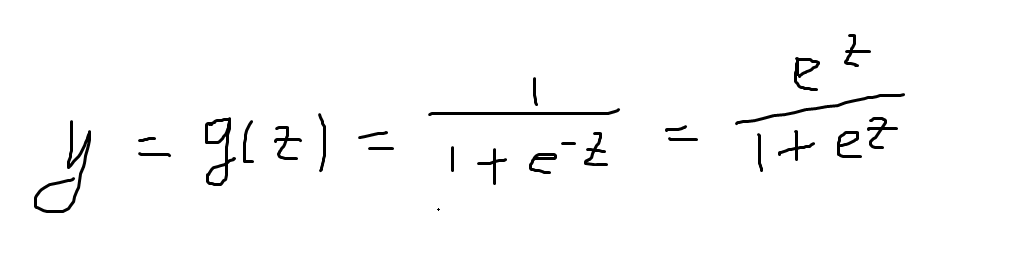
在变换一下

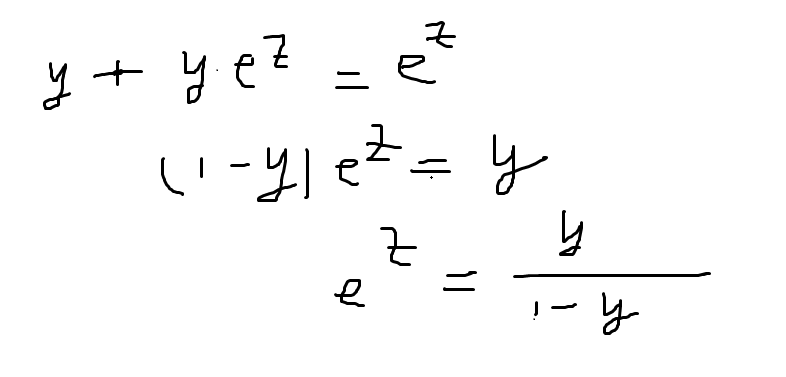
两边取对数

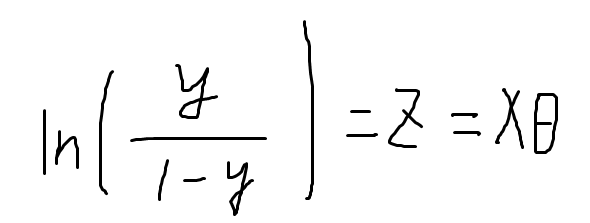
1.式子左边，y是逻辑回归输出，y处于[0,1]之间，y代表一个概率，代表输入样本x是正例的概率，1-y就是样本负例的概率 ,y/1-y是叫做几率，几率反应了反映了x作为正例的相对可能性;求对数得到“对数几率”，又称logit，所以逻辑回归又称为对数几率回归。

由上式可以看出，实际是在用线性回归模型的结果逼近真实标记的对数几率

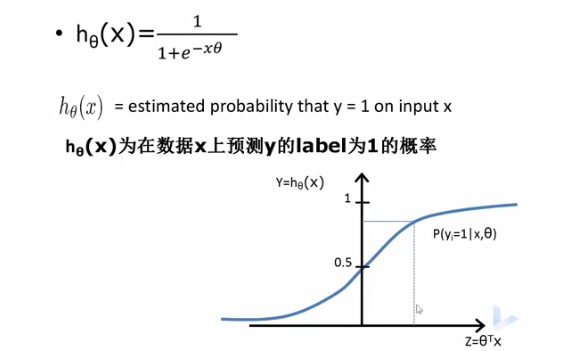
比如以肿瘤预测为例子:

1. x是输入
2. x0恒为1
3. x1是大小
4. hθ=0.7代表70%的几率该肿瘤是恶性的

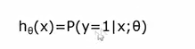
得到结果可以写为在给定样本和参数情况下，输出为1的概率，也称输出为1的概率为0.7，因此用逻辑回归做分类，不仅可以告诉我们属于那个类，还可以告诉我们属于该类的概率多大。

logistic回归的决策边界

什么是决策边界：决策边界是处在边界上的一些点在二分类的时候被分为正例或者负例的几率是一样的

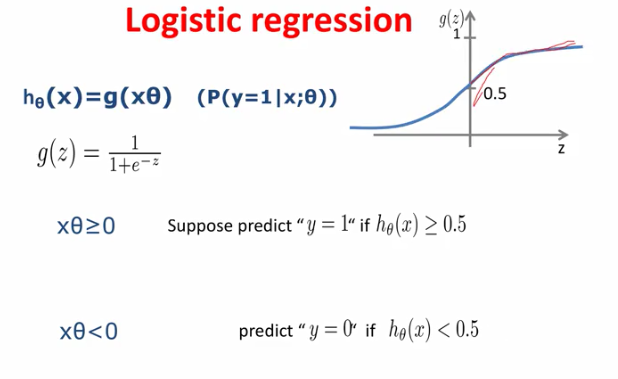
1.xθ是线性回归的预测结果，当其值>0的时候，经过logistics函数之后输出>0.5,也就是预测其为正例的概率>0.5
2.xθ是线性回归的预测结果，当其值<0的时候，经过logistics函数之后输出<0.5,也就是预测其为正例的概率<0.5
3.xθ是线性回归的预测结果，当其值=0的时候，经过logistics函数之后输出=0.5,也就是预测其为正例的概率=0.5,和预测负例概率一样

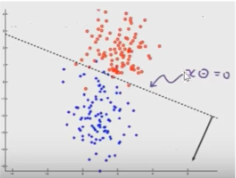
二维平面上：xθ是一条直线，在它上面的点属于正例，在它下面的点属于负例

多维情况下：

1.线性模型y=θ0+θ1x1+θ2x2
2.当参数依次是[-3,1,1]的时候，令其为0，得到 -3+x1+x2=0
3.绘制该直线再平面上，可以看出该直线将样本分开了，直线上面的是正样本，直线下面的是负样本

更高维度的空间：比如三维，决策边界是一个平面，该平面上面正类，下面是负类

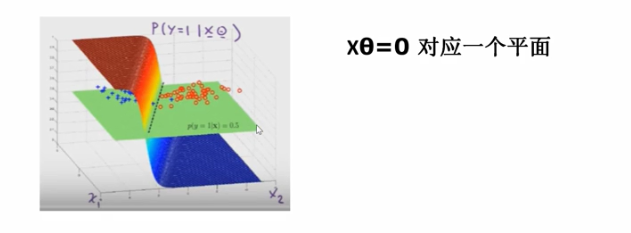
更高维度的空间，比如n维，我们是画不出来的，但是我们可以想象有一个超平面将正样本和负样本分开。

非线性决策边界

若特征组合是非线性函数(多项式)，那么它的决策边界是怎样的？
例如：

我们代入参数并令该函数为0得到，决策边界是一个球面，对应到二维是一个圆：

如果我们的模型是一个更复杂的模型，那么得到的决策边界会更复杂：

逻辑回归的代价函数

1.我们有包含m个训练样本的监督训练集:

2. 其中每个x写出列向量的形式：x0为1，y是[0,1]也就是分类结果

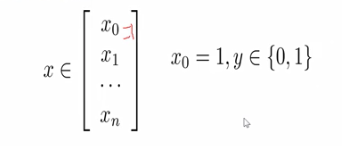
3. 我们的假设为:

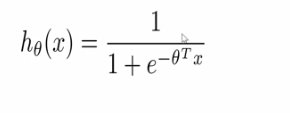
4. 问题是找到参数，使得模型假设都能输出正确的值，所以要构造损失函数

我们已知线性回归函数的损失函数：

逻辑回归的损失函数也能用线性回归的损失函数吗？

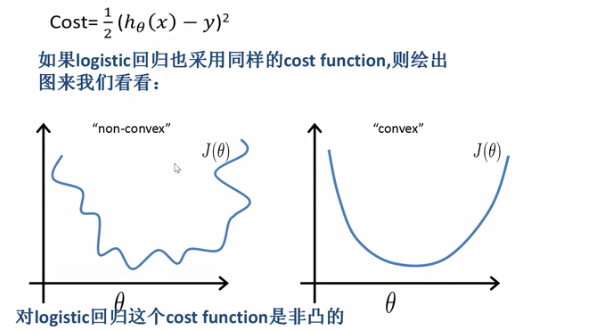
1.对logistic回归这个cost function是非凸的
2.对于凸优化我们有现成的算法，非凸函数不好优化

逻辑回归的损失函数是：

1. 样本真实label是1的话，hθ代表模型输出，我们希望模型输出尽可能接近1，如果模型预测输出特别接近1的话，那么损失的函数的值就接近于0代价非常少，也就是惩罚很小，如果这种情况下，hθ输出非常的接近于0的数，那么损失函数的值就会究极大，惩罚很大

2. 样本的真实值为0的情况下，我们希望模型输出接近于0，如果模型输出接近于0，那么损失函数值很小，否则就很大

总之，如果输出与预期不一致的话，损失函数的值就会特别的大，也就是惩罚特别大，否则的话惩罚就会很小，损失函数的值就会非常小。

该损失函数是一个分段函数，但是实际上我们求导的过程中，并不希望其是分段函数，所以将其合起来：

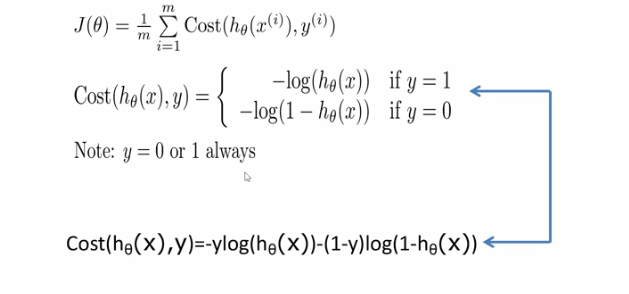
这个损失函数有一个名字叫做交叉熵损失函数。

我们接下来希望基于这个损失函数进行优化：

梯度下降算法来进行求解函数的参数：

对损失函数求导：

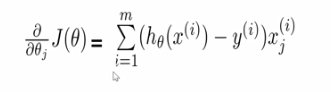
推导过程：

确定了cost function之后，寻找参数θ，使得cost_function的值取得最小也就是优化问题

优化方法对比

其他优化算法不需要手工确定学习率，速度比梯度下降快，缺点是更复杂！

回顾

对于之前知识的回顾：

岭回归在线性回归的基础上，应用岭回归的情况通常是特征数>样本数、或者是有冗余特征的情况下。岭回归损失函数在线性回归基础上引入了正则化项。

对数几率回归是将线性回归的基础上将其输出输入到一个logistics函数中去，变换得到预测样本为正例的概率值。

逻辑回归的损失函数是交叉熵损失函数：

之所以该函数叫做交叉熵损失函数，log（）里面用的概率并不是真实的概率，而是模型输出的概率，存在误差

决策边界

决策边界取决于特征之间的组合，比如线性组合或者非线性组合。一个更加复杂的特征组合，对应更为复杂的决策边界。

多项式组合可以推广为线性组合，通过令z1等于x1，z2等于x2^2,...的形式转换为线性组合，相当于在z空间的特征的线性组合，对于每一个特征x用函数给变换一下，这个函数就叫做基函数，基函数也有很多种。

线性回归模型的样本点(x,y) 的y服从什么样的分布?

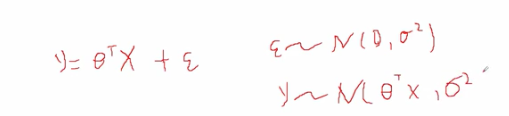
1. 线性回归样本点都不是一定在直线上，都存在一定的误差
2. 误差服从均值为0，方差为σ^2的高斯分布
3. y也是符合高斯分布的，均值为直线，方差为σ^2

线性模型:
X:输入特征X和X;之间互相独立
y:服从高斯分布，y之间也相互独立

广义线性回归

1. 广义线性回归的表达式和线性回归的表达式是一样的
2. 不一样的是左边，我们用特征组合逼近的不是y，而是y的一个函数

广义线性回归是一个大的框架，之前的线性回归，logistics回归都可以归到里面来。y服从指数族分布包括很多种分布。

例如线性回归:

1. y服从高斯分布
2. 特征线性组合逼近y
3. 对y进行变换，就是它本身

逻辑回归:

1. y因为要么0要么1，服从伯努利分布
2. 线性组合来逼近用链接函数变换过的y，链接函数是对数几率函数

正则化的logistics回归

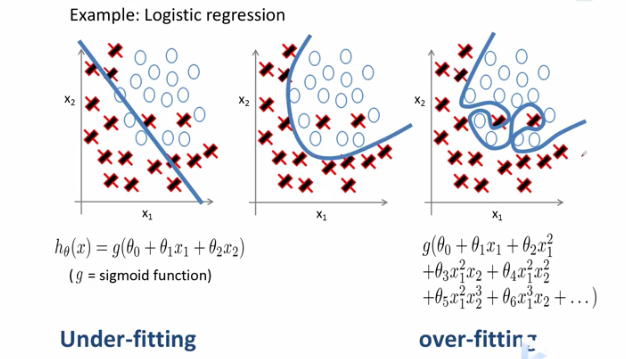
我们希望学到的决策边界既不过于简单（欠拟合），更不特别复杂（过拟合）。

前面我们学过可以通过增加正则化项来防止过拟合，减少高次项的参数θ的值，使得曲线平滑

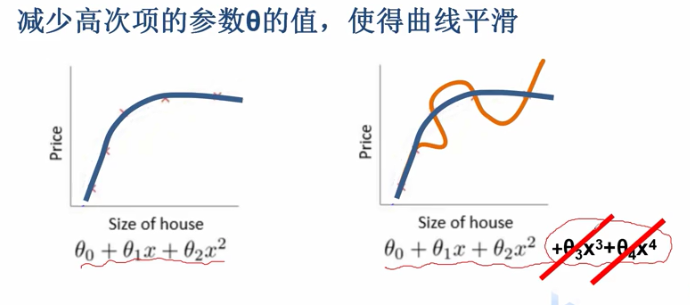
对于逻辑回归回归我们增加了正则化项来防止过拟合:

进而梯度下降算法改写：

逻辑回归做多分类问题

什么是多分类？

区分猫狗小鸡

对邮件分类：

对天气分类

Logistic回归多分类

逻辑回归主要适用于二分类问题如何让其适用于多分类呢？

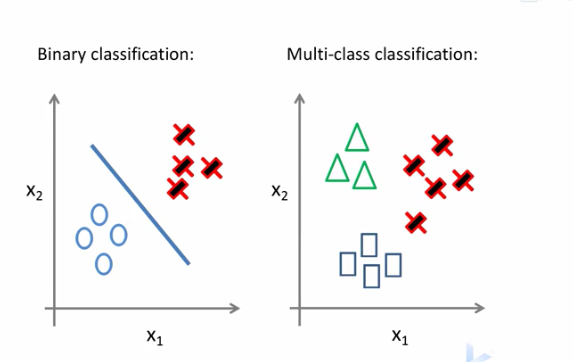
1. 将一类作为正样本，其他类作为负样本

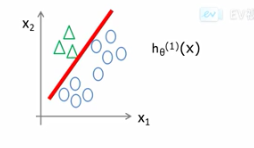
2. 同理将第二类作为正例，其他类作为负类

3. 同理将第n类作为正例，其他类作为负类

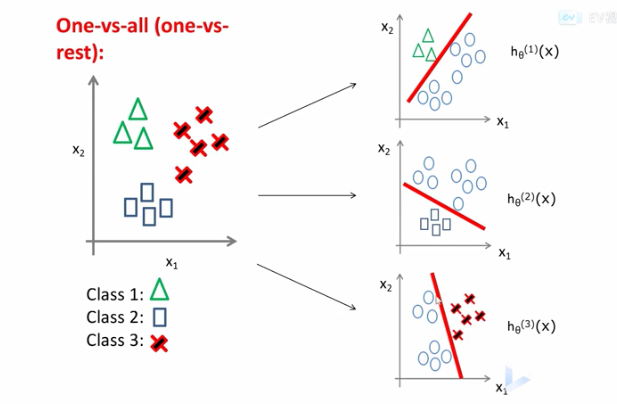
• 对每个类依次训练logistics回归分类器预测当前样本属于哪个类
• 对于一个新的样本，依次将该样本输入三个分类器，选择概率最大的那个类，即最可能的属于的类

Softmax回归多分类

1. 分母是分子所有情况的和
2. 给定一个模型，比如神经网络模型，分l类，最后会输出l个数值
3. l个数值作为向量输入到softmax函数中，将数值转化到概率分布上去
4. f1....fn代表概率
5. 选择最大概率对应的类，就是最终属于的类