这篇文章主要给一些不太喜欢数学的朋友们的,其中基本没有用什么数学公式。
目录
- 直观理解主题模型
- LDA的通俗定义
- LDA分类原理
- LDA的精髓
- 主题模型的简单应用-希拉里邮件门
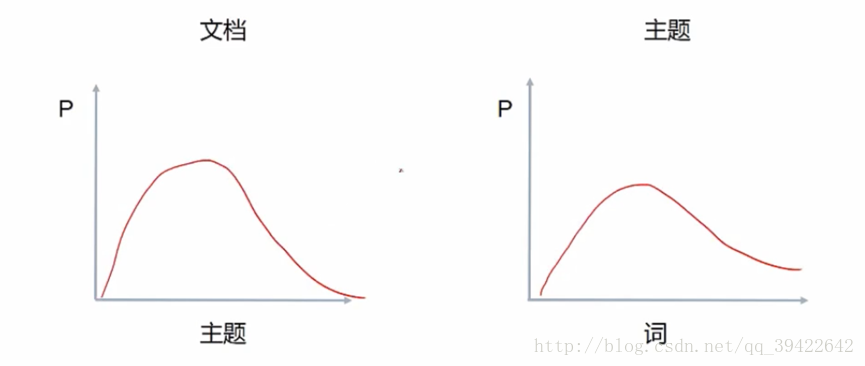
1.直观理解主题模型
听名字应该就知道他讲的是什么?假如有一篇文章text,通过里面的词,来确定他是什么类型的文章,如果文章中出现很多体育类的词,比如,篮球,足球之类的,那么主题模型就会把它划分为体育类的文章。
因为主题模型涉及比较多的数学推导,所以我们先用一个小栗子,理解它要做的事。假设有这么一个场景:
- 一个资深HR收到一份应聘算法工程师的简历,他想仅仅通过简历来看一下这个人是大牛,还是彩笔,他是怎么判断呢?
他的一般做法就是拿到这份简历,看这个人的简历上写的内容包括了什么?
在此之前呢,他也一定是接触了很多算法工程师的面试,他根据这些招进来的人判断,一个大牛,有可能是:
- 穿条纹衬衫
- 曾在BAT就职
- 做过大型项目
这个HR就会看这个面试者是不是穿条纹衬衫,有没有在BAT就职过,做过什么牛逼的项目,如果都满足条件,那这个HR就会判断这个人应该是大牛,如果他只是穿条纹衬衫,没做过什么拿得出手的项目,那就要犹豫一下了,因为他是彩笔的可能性比较大。
这个例子和主题模型的关系可以用这个图表示:
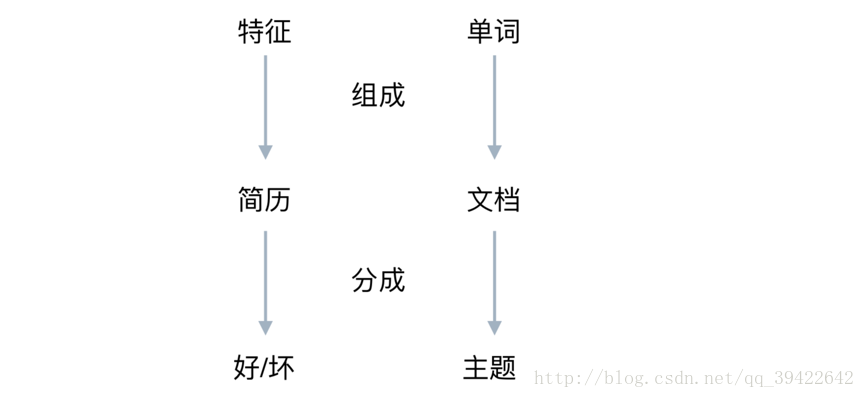
在LDA眼里,相当于是词袋,每个袋子里都有一堆词,用的时候就只管检测这些词出现与否就OK了。
用公式可以表示成:
2.LDA的通俗定义
什么是LDA?
- 它是一种无监督的贝叶斯模型。
- 是一种主题模型,它可以将文档集中的每篇文档按照概率分布的形式给出。
- 是一种无监督学习,在训练时不需要手工标注的训练集,需要的是文档集和指定主题的个数。
- 是一种典型的词袋模型,它认为一篇文档是由一组词组成的集合,词与词之间没有顺序和先后关系。
它主要的优点就是可以对每个主题,都找出一些词来描述它。
3.LDA分类原理
先前详细写过贝叶斯模型的原理以及它所代表的思想,详细请戳:神奇的贝叶斯思想,这里只简单说一下它的原理,用在这里的意思是:
经过一系列推导,可以得到这样一个链式的关系:
也就是:
这样的关系。
同一主题下,某个词出现的概率,以及同一文档下,某个主题出现的概率,两个概率的乘积,可以得到某篇文档出现某个词的概率,我们在训练的时候,调整这两个分布就可以了。
由此可以定义LDA的生成过程:
- 对每篇文档,在主题分布中抽取一个主题;(相当于左图)
- 对抽到的主题所对应的单词分布中随机抽取一个单词;(在右图中抽)
- 重复上述过程直至遍历整篇文档中的每个单词
经过以上三步,就可以看一下两个分布的乘积,是否符合给定文章的分布,以此来调整。
稍微具体点讲: (w代表单词;d代表文档;t代表主题; 大写代表总集合,小写代表个体。)
D中每篇文档d看作个单词序列:
,wi表示第i个单词。
D中涉及的所有不同单词组成一个词汇表大集合V (vocabulary),LDA以文档集合D作为输入,希望训练出的两个结果向量 (假设形成k个topic,V中共有m个词):
- 结果向量1:对每个D中的文档d,对应到不同主题的概率θd
:
<pt1,...,ptk>其中pti 表示d对应k个主题中第i个主题的概率,计算的方法也很简单:pti=d中有多少个词是第i个主题也有的d中所有词的总数
- 结果向量2:对每个T中的主题t
,生成不同单词的概率向量ϕt
:
<pw1,...,pwm>其中pwi 表示主题t 生成V中第i个单词的概率。计算方法:pwi=主题t对应到V中第i个单词出现的次数主题t下的所有单词总数
4.LDA的精髓
说了那么多,其实LDA的核心,仍然是这个公式:
用表达式如下:
其实就是以主题为中间层,通过前面的两个向量(θd ,ϕt ),分别给出P(w|t),P(t|d) ,它的学习过程可以表示为:
- LDA算法开始时,先随机地给θd ,ϕt 赋值(对所有的d和t)
- 针对特定的文档ds
中的第i单词wi
,如果令该单词对应的主题为tj
,可以把 上述公式改写为:
Pj(wi|ds)=P(wi|tj)∗P(tj|ds)
- 枚举T中的主题,得到所有的pj(wi|ds) .然后可以根据这些概率值的结果为ds 中的第i个单词wi 选择一个主题,最简单的就是取令Pj(wi|ds) 概率最大的主题 tj 。
- 如果ds 中的第i个单词wi 在这里选择了一个与原先不同的主题,就会对θd ,ϕt 有影响,他们的影响反过来影响对上面提到的p(w|d) 的计算。
对文档集D中的所有文档d中的所有w进行一次p(w|d) 计算,并重新选择主题看成是一次迭代。迭代n次之后就可收敛到LDA所需要的分类结果了。
5.主题模型的简单应用-希拉里邮件门
我们如果不想要具体了解具体的数学公式推导,理解到这里就差不多了,重点是学会怎么使用?
我们用希拉里邮件门那个案例,看一下应该怎么使用gensim来进行邮件分类。
from gensim import corpora, models, similarities
import gensim
import numpy as np
import pandas as pd
import re
df = pd.read_csv("../input/HillaryEmails.csv")
# 原邮件数据中有很多Nan的值,直接扔了。
df = df[['Id','ExtractedBodyText']].dropna()
df.head()数据样式:
做一个简单的预处理:
def clean_email_text(text):
text = text.replace('
'," ")
text = re.sub('-'," ",text)
text = re.sub(r"d+/d+/d+", "", text) #日期,对主体模型没什么意义
text = re.sub(r"[0-2]?[0-9]:[0-6][0-9]", "", text) #时间,没意义
text = re.sub(r"[w]+@[.w]+", "", text) #邮件地址,没意义
text = re.sub(r"/[a-zA-Z]*[://]*[A-Za-z0-9-_]+.+[A-Za-z0-9./%&=?-_]+/i", "", text) #网址,没意义
pure_text = ''
for letter in text:
if letter.isalpha() or letter ==' ':
pure_text += letter
text = ' '.join(word for word in pure_text.split() if len(word)>1)
return text
docs = df['ExtractedBodyText']
docs = docs.apply(lambda x :clean_email_text(x))
看一下处理成啥样的:
docs.head(2).values处理成一个一个词了
即:
手写的停用词,这还有各色的别人写好的停用词:stopwords
stoplist = ['very', 'ourselves', 'am', 'doesn', 'through', 'me', 'against', 'up', 'just', 'her', 'ours',
'couldn', 'because', 'is', 'isn', 'it', 'only', 'in', 'such', 'too', 'mustn', 'under', 'their',
'if', 'to', 'my', 'himself', 'after', 'why', 'while', 'can', 'each', 'itself', 'his', 'all', 'once',
'herself', 'more', 'our', 'they', 'hasn', 'on', 'ma', 'them', 'its', 'where', 'did', 'll', 'you',
'didn', 'nor', 'as', 'now', 'before', 'those', 'yours', 'from', 'who', 'was', 'm', 'been', 'will',
'into', 'same', 'how', 'some', 'of', 'out', 'with', 's', 'being', 't', 'mightn', 'she', 'again', 'be',
'by', 'shan', 'have', 'yourselves', 'needn', 'and', 'are', 'o', 'these', 'further', 'most', 'yourself',
'having', 'aren', 'here', 'he', 'were', 'but', 'this', 'myself', 'own', 'we', 'so', 'i', 'does', 'both',
'when', 'between', 'd', 'had', 'the', 'y', 'has', 'down', 'off', 'than', 'haven', 'whom', 'wouldn',
'should', 've', 'over', 'themselves', 'few', 'then', 'hadn', 'what', 'until', 'won', 'no', 'about',
'any', 'that', 'for', 'shouldn', 'don', 'do', 'there', 'doing', 'an', 'or', 'ain', 'hers', 'wasn',
'weren', 'above', 'a', 'at', 'your', 'theirs', 'below', 'other', 'not', 're', 'him', 'during', 'which']分词:
texts = [[word for word in doc.lower().split() if word not in stoplist] for doc in doclist]
texts[0]
当然还可以用包,比如jieba,bltk.
得到的就是一篇文档一个词袋。
建立预料库:每个单词用数字索引代替,得到一个数组。
dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]得到:

这个列表告诉我们,第14(从0开始是第一)个邮件中,一共6个有意义的单词(经过我们的文本预处理,并去除了停止词后)
其中,36号单词出现1次,505号单词出现1次,以此类推。。。
接着,我们终于可以建立模型了:
lda = gensim.models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=20)
lda.print_topic(10, topn=5)得到第10号分类中,最常见的单词是:
- ‘0.007*kurdistan + 0.006*email + 0.006*see + 0.005*us + 0.005*right’
把五个主题打出来看一下:
lda.print_topics(num_topics=5,num_words =6)有空可以练一下gesim:
gensim使用指南
详细的推导:数学公式版下一篇文章介绍
参考:七月在线