DS博客作业02--栈和队列

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业02--栈和队列
这个作业的目标	学习栈和队列的结构设计及运算操作
姓名	廖浩轩

0.PTA得分截图

1.本周学习总结

1.1 栈

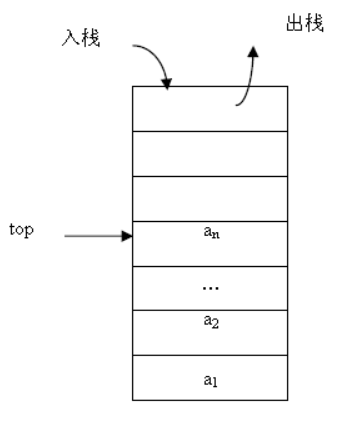
• 顺序栈：用一段连续的存储空间来存储栈中的数据元素，比较常见的是用数组来实现顺序栈

栈的声明

typedef struct sta
 {
     int *top;            /* 栈顶指针 */
     int *bottom;        /* 栈底指针 */
     int stack_size;        /* 栈的最大容量 */
 }stack;

栈的初始化

  stack InitStack (stack p)
  {
      p.bottom = (int *)malloc(p.stack_size * sizeof(int));
      if (p.bottom == NULL)
      {
          printf("初始化栈失败
");
          exit(0);
      }
     p.top = p.bottom;
     p.stack_size = MAX_SIZE;
 
     return p;
 }

入栈

stack Push (stack p)
  {
      int data;
      if (StackFull(p) == Full)
      {
          printf("栈空间已满，无法入栈");
          return p;
      }
     printf("Please input data");
     scanf("%d", &data);
     *p.top = data;
     p.top++;
 
     return p;
  }

出栈

stack Pop (stack p)
 {
     if (StackEmpty(p) == Empty)
     {
         printf("栈为空栈，无法出栈 ");
         return p;
     }
     p.top--;
     printf("出栈元素为：%d
", *p.top);
 
     return p;
 }

判断栈是否为空

int StackEmpty (stack p)
 {
     if (p.top == p.bottom)
     {
         return Empty;
     }
     else
     {
         return Avail;
     }
 }

判断栈是否为满

int StackFull (stack p)
 {
     if (p.top - p.bottom == p.stack_size)
     {
         return Full;
     }
     else
     {
         return Avail;
     }
 }

遍历栈中的元素

void DisplyStack (stack p)
 {
     if (StackEmpty(p) == Empty)
     {
         printf("栈为空栈，无法遍历
");
         return;
     }
     printf("栈中元素为：");
     printf("顶端[");
     while (p.top != p.bottom)
     {
         p.top--;
         printf("%d-", *p.top);
     }
     printf("]底端
");
 }

• 链栈：链式栈中的元素以Node的形式存储，节点Node中存有此节点存于栈中的元素以及指向下个节点的指针

栈的声明

typedef struct node 
{
	SElemType  data;//数据域
	struct node *next;//指针域
}LinkStackNode;

入栈

Status Push(LinkStackNode *top, SElemType x) 
{
	LinkStackNode * p;
	p = (LinkStackNode *)malloc(sizeof(LinkStackNode));
	if (!p)  return ERROR;    
	p->data = x;
	p->next = top->next;
	top->next = p;    
	return OK;
}

出栈

Status Pop(LinkStackNode *top, SElemType *x)
{  
	LinkStackNode * p;
	p = top->next;
	if (p == NULL)   
		return OVERFLOW;
	top->next = p->next;
	*x = p->data;
	free(p);    
	return OK;
}

1.2 栈的应用

• 数制转换

十进制数N和其他d进制数的转换是计算机实现计算的基本问题，其解决方法很多，同样用栈也可以解决
下述算法实现了十进制数转八进制数，并打印结果

public class Conversion 
{
    public static void conversion(int N) 
    {
        ArrayStack<Integer> stack = new ArrayStack<>();
        while (N != 0) 
        {
            stack.push(N % 8);
            N /= 8;
        }
        while (!stack.isEmpty()) 
        {
            System.out.print(stack.pop());
        }
    }

    public static void main(String[] args) 
    {
        conversion(2007);
    }
}

• 括号匹配检验

假设表达式中包含三种括号：圆括号、方括号和花括号，并且它们可以任意嵌套。例如{()[{}]}或[{()}([])]等为正确格式，而{[}()]或[({)]为不正确的格式。
于是我们可以设计算法：算法需要一个栈，在读入字符的过程中，如果是左括号，则直接入栈，等待相匹配的同类右括号；如果是右括号，且与当前栈顶左括号匹配，则将栈顶左括号出栈，如果不匹配则属于不合法的情况。另外，如果碰到一个右括号，而堆栈为空，说明没有左括号与之匹配，则非法。那么，当字符读完的时候，如果是表达式合法，栈应该是空的，如果栈非空，那么则说明存在左括号没有相应的右括号与之匹配，也是非法的情况。
下述算法实现了对该表达式的括号匹配检验

public class Match 
{
    public static boolean match(String s) 
    {
        ArrayStack<Character> stack = new ArrayStack<>();
        for (int i = 0; i < s.length(); i++) 
        {
            char c = s.charAt(i);
            switch (c) 
            {
            case ')':
                if (!stack.isEmpty() && stack.pop() == '(') 
                {
                    break;
                }
                else 
                {
                    return false;
                }
            case ']':
                if (!stack.isEmpty() && stack.pop() == '[')
                {
                    break;
                }
                else 
                {
                    return false;
                }
            case '}':
                if (!stack.isEmpty() && stack.pop() == '{') 
                {
                    break;
                }
                else 
                {
                    return false;
                }
            default:
                stack.push(c);
                break;
            }
        }
        return stack.isEmpty();
    }

    public static void main(String[] args)  
    {
        System.out.println(match("{[()]()[{}]}"));
        System.out.println(match("{[()]}}"));
    }
}

• 迷宫求解

求迷宫从入口到出口的所有路径是一个经典的程序设计问题。由于计算机解迷宫时，通常用的是“穷举求解”的方法，即从入口出发，顺某一方向向前探索，若能走通，则继续往前走；否则沿原路退回，换一个方向再继续探索，直至所有可能的通路都探索到为止。
为了保证在任何位置都能沿原路退回，显然需要用一个后进先出的结构来保存从入口到当前位置的路径。因此在迷宫求解时应用“栈”也就是自然而然的事情了。
在计算机中，我们可以用一个二维数组来表示一个迷宫
求解迷宫的算法思想的伪代码

初始化，将起点加入堆栈；
while(堆栈不为空)
{
    取出栈顶位置为当前位置；
    如果 当前位置是终点，
    则 使用堆栈记录的路径标记从起点至终点的路径；
    否则
    {
        按照从下、右、上、左的顺序将当前位置下一个可以探索的位置入栈；
        如果 当前位置的四周均不通
        则 当前位置出栈；
    }
}

1.3 队列

• 顺序队列：队列的这种头尾相接的顺序存储结构称为循环队列。

队列声明

#define MAXSIZE  5    //最大容量是5个元素
struct queue   //队列

{
       int a[MAXSIZE];   //队列元素
       int front;          //队头
       int rear;           //队尾
};

判断循环队列是否为空

int SeQueue::Empty()
{ 
if(rear==front) return(1);
else return(0);
}

在循环队列中插入新的元素x

void SeQueue::AddQ(ElemType x)
{
	if ((rear + 1) % MAXSIZE == front)
		cout << " QUEUE IS FULL! " << endl;
	else
	{
		rear = (rear + 1) % MAXSIZE;
		elem[rear] = x;
		cout << " OK!";
	}
}

删除队列中队首元素

ElemType SeQueue::DelQ()
{
	if (front == rear)
	{
		cout << " QUEUE IS EMPTY! " << endl; return -1;
	}
	else 
	{
		front = (front + 1) % MAXSIZE;
		return(elem[front]);
	}
}

取队列中的队首元素

ElemType SeQueue::Front()
{
	ElemType x;
	if (front == rear)
		cout << "QUEUE IS EMPTY " << endl;
	else 
		x = elem[(front + 1) % MAXSIZE];
	return (x);
}

• 环形队列:
  

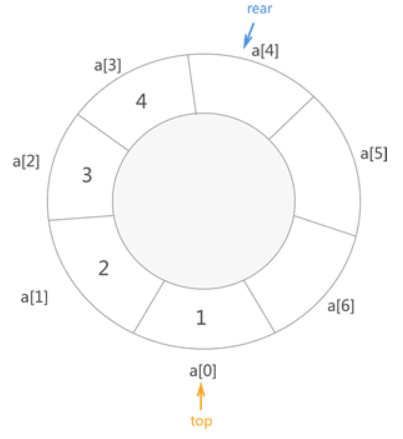
队列声明

typedef struct
{
	ElemType data[Max]; 
	int front;   
	int count;   
}QueueType;

初始化队列

void InitQueue(QueueType *&q)
{
	q = (QueueType *)malloc(sizeof(QueueType));
	q->front =0;
	q->count =0;
}

判断队列是否为空

void  EmptyQueue(QueueType *q)
{
	if (q->count==0)
		cout<< "队列为空！" << endl;
	else
		cout << "队列不为空！" << endl;
}

元素进队

int enQueue(QueueType*& q, ElemType x)
{
	int rear;
	if (q->count == Max) //队满溢出
		return 0;
	else
	{
		rear = (q->front + q->count) % Max;
		rear = (rear + 1) % Max;
		q->data[rear] = x;
		q->count++;
		return 1;
	}
}

元素出队

int deQueue(QueueType *&q,ElemType &x)
{
	if(q->count==0)
		return 0;
	else
	{
		q->front=(q->front+1)%Max;
		x=q->data[q->front];
		q->count--; 
	}
}

输出队列的元素个数

void LenghtQueue(QueueType *q)
{
	cout << q->count << endl;
}

释放队列

void DestroyQueue(QueueType *q)
{
	free(q);
}

• 链队列:
  

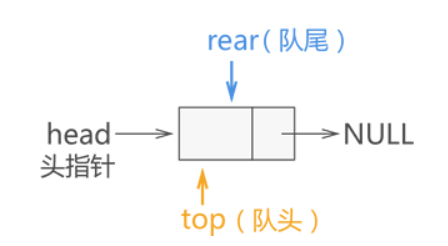
队列声明

typedef struct QNode
{
    int data;
    struct QNode * next;
}QNode;

创建队列

QNode* initQueue() 
{
    QNode* queue = (QNode*)malloc(sizeof(QNode));
    queue->next = NULL;
    return queue;
}

入队

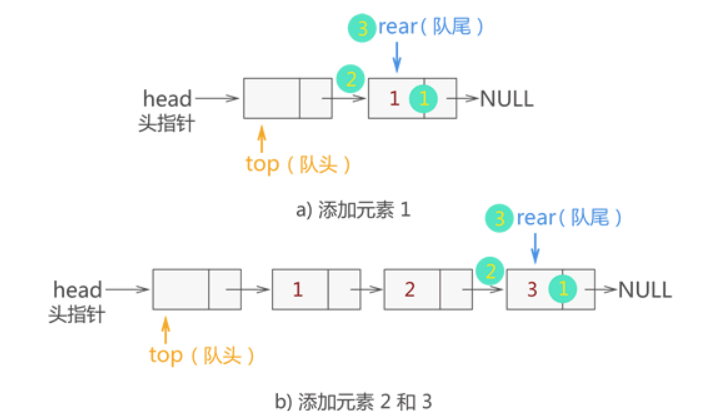
QNode* enQueue(QNode* rear, int data) 
{
    QNode* enElem = (QNode*)malloc(sizeof(QNode));
    enElem->data = data;
    enElem->next = NULL;
    rear->next = enElem;
    rear = enElem;
    return rear;
}

出队

void DeQueue(QNode* top, QNode* rear)
{
    if (top->next == NULL) 
    {
        printf("队列为空");
        return;
    }

    QNode* p = top->next;
    printf("%d", p->data);
    top->next = p->next;
    if (rear == p) 
    {
        rear = top;
    }
    free(p);
}

• 队列应用

2.PTA实验作业

• 代码上传码云没整明白，所以还是截图代码了，下次一定整明白

2.1 符号配对

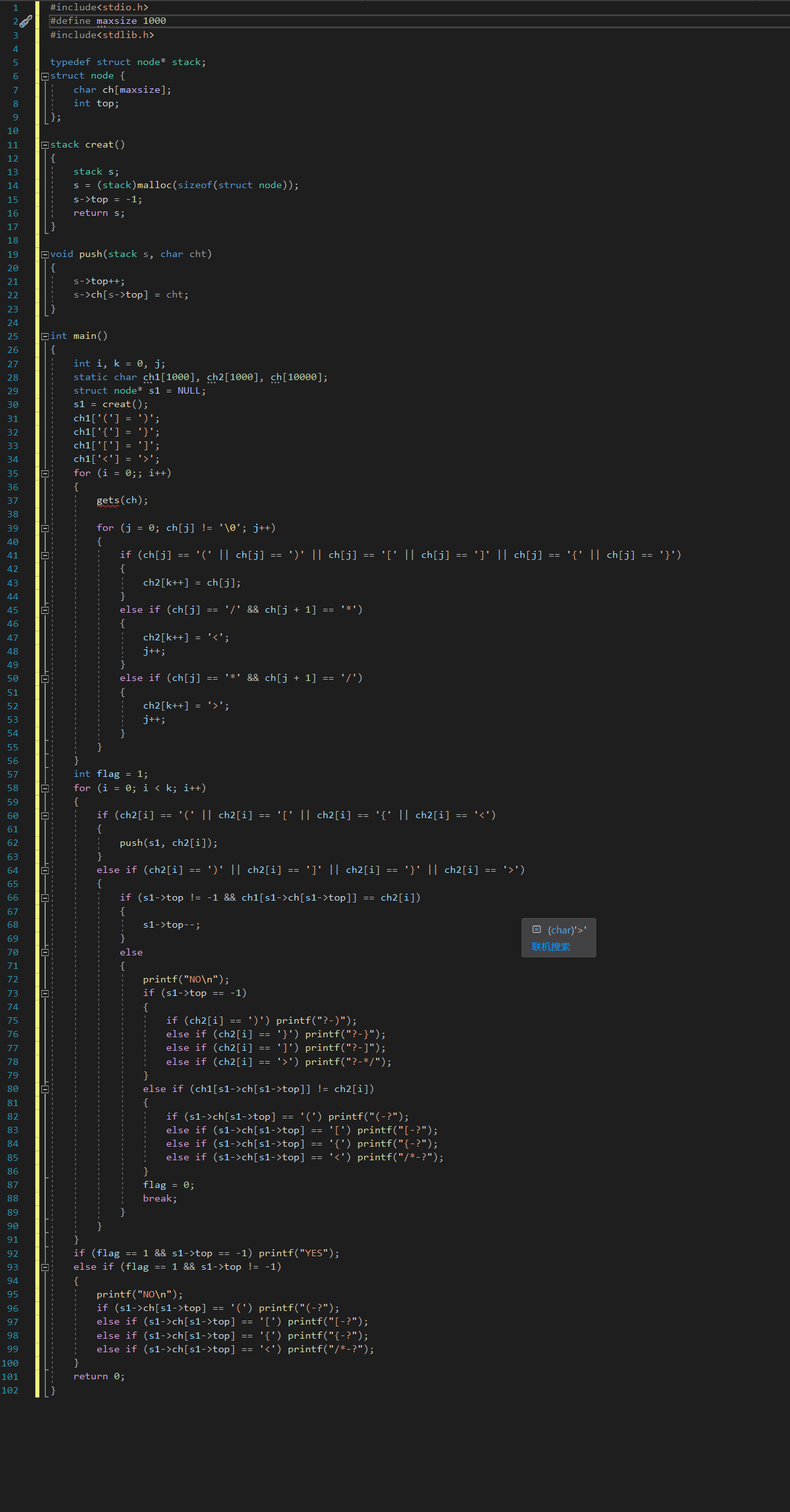
2.1.1 解题思路及伪代码

解题思路：把比较特殊的/和/用< >代替，创建一个栈然后把找到的对应符号放入栈中，然后进行比较得到符号是否匹配

int main
{
  static char ch1[1000], ch2[1000], ch[10000];//ch放代码，ch2放找到的符号，ch1用于符号匹配
for(i = 0;; i++)
  {
    找到对应符号然后放入ch2中//用<>代替两个的符号
  }
int flag=1 用于记录
for (i = 0; i < k; i++)
  {
    if ch2中符号是左符号，放入栈中
    else if ch2中符号是右符号
    {
      if 栈中存在符号，并且和ch2和栈中符号匹配，则消除栈中该符号
      else 输出NO 和对应缺少的符号，flag=0
    }
  }
if flag=1同时栈中无符号 输出YES
else
  {  输出  NO
     根据栈中情况输出对应缺少符号
  }
}

2.1.2 总结解题所用的知识点

栈的出栈和入栈，栈指针的变化来判断栈中元素变化

2.2 银行业务队列简单模拟

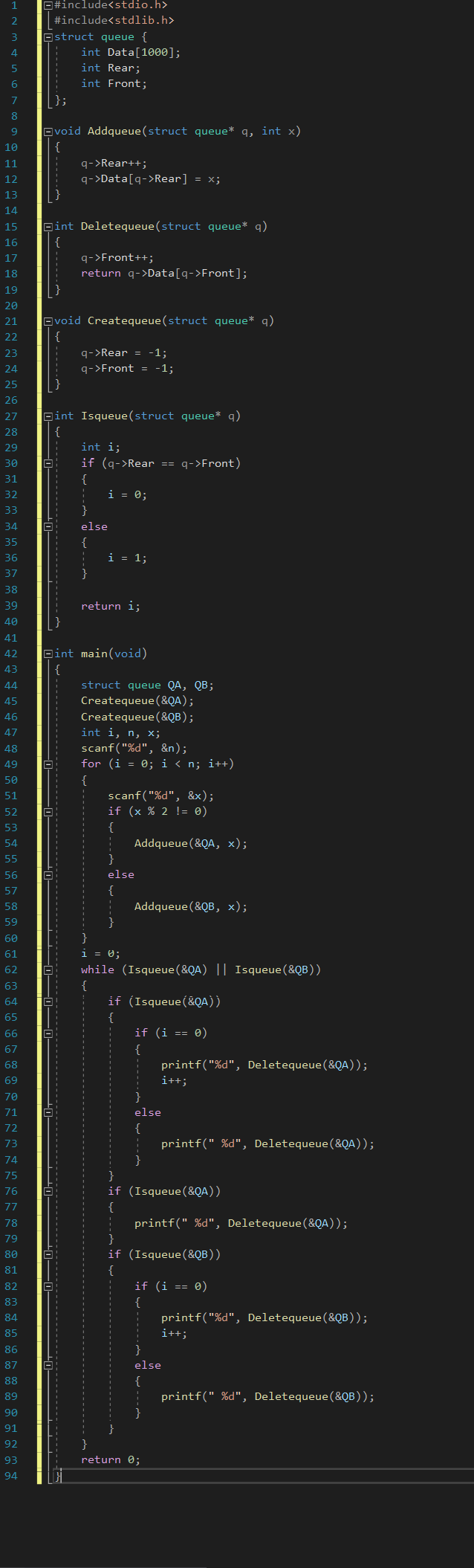
2.2.1 解题思路及伪代码

解题思路：依题意得A总比B先输出，且当A中含有元素时总先输出两个，所以按照2：1的比例输出AB中的数，用队列来表示就是出队操作

int main
{
struct queue QA, QB;//创建两个队列
Createqueue(&QA);
Createqueue(&QB);

scanf("%d", &n);
for (i = 0; i < n; i++)
{
  if是奇数 放入队列QA  
  else 放入队列QB
}
while 两个队列不同时为空
{
  if QA不为空 输出QA中的数，同时出队
  if QA不为空 输出QA中的数，同时出队
  if QB不为空 输出QB中的数，同时出队
}

2.2.2 总结解题所用的知识点

队列的出队和入队

3.阅读代码

3.1 题目及解题代码

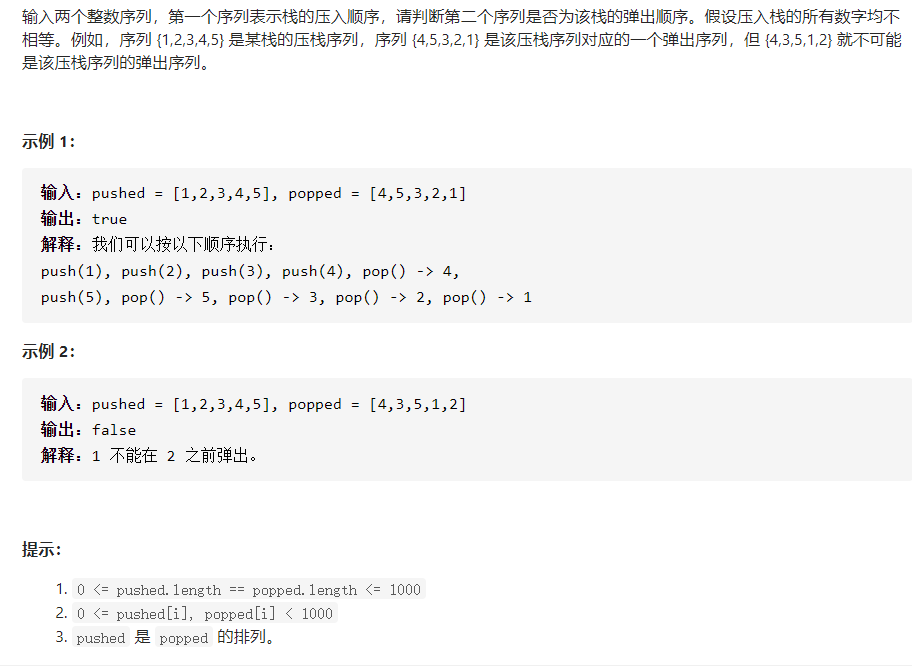
解题代码

class Solution:
    def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
        stack, i = [], 0
        for num in pushed:
            stack.append(num) # num 入栈
            while stack and stack[-1] == popped[i]: # 循环判断与出栈
                stack.pop()
                i += 1
        return not stack

3.2 该题的设计思路及伪代码

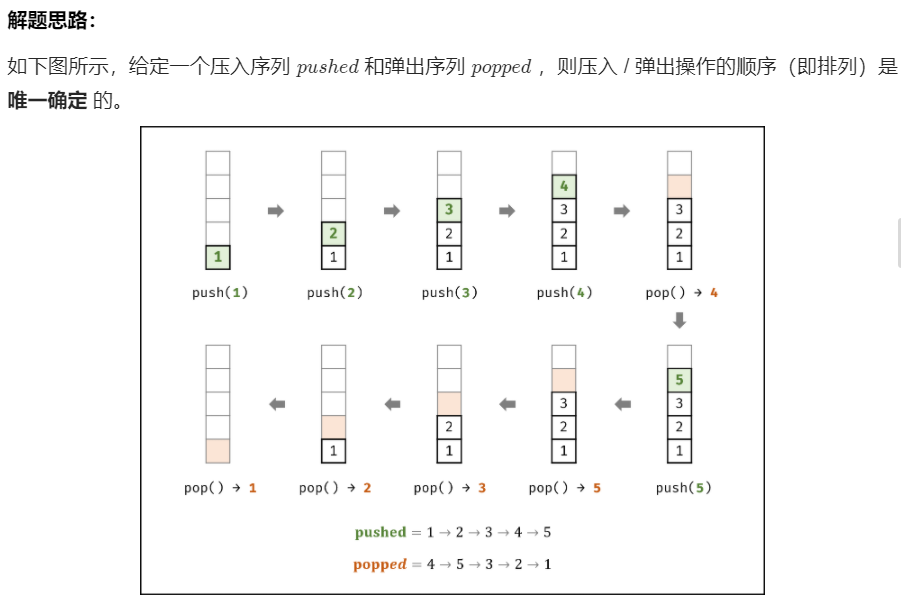
3.3 分析该题目解题优势及难点

由于题目规定 栈的所有数字均不相等 ，因此在循环入栈中，每个元素出栈的位置的可能性是唯一的（若有重复数字，则具有多个可出栈的位置）。因而，在遇到 “栈顶元素 == 弹出序列的当前元素” 就应立即执行出栈。
先找到进栈中最后一个（我叫做标准值），在出栈之后的的所有元素，都只会在这个值后面。所以在出栈数列中最后一个进栈的数字后面一定是递减的。可以来排个序。对于这个标准值前面的数字呢？如果说前一个数字比后一个数字小没什么关系，但是如果说前面数字比后面数字大就要讨论一下了。
就拿[0,1,2,3,4,5,..,12]和[0,4,3,5,2,1，7，8，10，11，9，6]看这个地方有个5，比后面的2要大。我们已经看到0，3，4已经出栈了。那么现在栈呢剩下的就是[1,2]我们不能选1，中间隔着2，所以我们要选择离5更近的一个数字。后面11比9大，这个时候栈内还有[6,9]选择离11更接近的9，最后就是剩下的6。