LeetCode142：Linked List Cycle II

题目：

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Follow up:
Can you solve it without using extra space?

解题思路：

判断链表有无环，可用快慢指针进行，快指针每次走两步，慢指针每次走一步，如果快指针追上了慢指针，则存在环，否则，快指针走到链表末尾即为NULL是也没追上，则无环。

为什么快慢指针可以判断有无环？

因为快指针先进入环，在慢指针进入之后，如果把慢指针看作在前面，快指针在后面每次循环都向慢指针靠近1，所以一定会相遇，而不会出现快指针直接跳过慢指针的情况。

如何找到环的入口点呢？

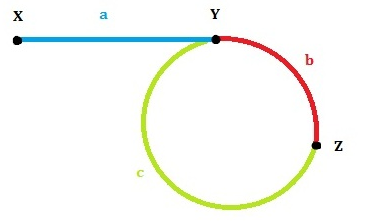
我们先看图再说话：

从图各段我们分析，因为quick指针每次走两步二slow指针每次走一步，所以当两指针相遇时，quick走了两倍的slow指针所走长度即：假设相遇点为z点

a + b + n * ( b + c ) = 2 * (a + b)  公式1

整理得：

a = n * (b + c) – b  公式2

根据公式2可知，要找到环入口点，可使用两个指针，p1和p2，p1从链表头开始走，p2从z点即快慢指针相遇点开始走，当p1指针走到Y（环入口点）时即长度为a时，p1走了n * (b + c) – b，可知p1也正好在Y点，所以利用p1和p2两指针，当它们相遇时，相遇点即为环入口点。

实现代码：

#include <iostream>
using namespace std;

/**
Linked List Cycle II
 */
 
struct ListNode {
     int val;
     ListNode *next;
     ListNode(int x) : val(x), next(NULL) {}
};
void addNode(ListNode* &head, int val)
{
    ListNode *node = new ListNode(val);
    if(head == NULL)
    {
        head = node;
    }
    else
    {
        node->next = head;
        head = node;
    }
}
void printList(ListNode *head)
{
    while(head)
    {
        cout<<head->val<<" ";
        head = head->next;
    }
}

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head == NULL || head->next == NULL)
            return NULL;
        ListNode *quick = head;
        ListNode *slow = head;
        while(quick && quick->next)//利用快慢指针判断有无环 
        {
            quick = quick->next->next;
            slow = slow->next;
            if(quick == slow)
                break;
        }
        if(quick != slow)
            return NULL;
        //slow指针从头开始走，quick指针从相遇点开始走，根据公式可知，相遇点即为环入口点 
        slow = head;
        while(slow != quick)
        {
            slow = slow->next;
            quick = quick->next;
        }
        return slow;                
    }
};
int main(void)
{
    ListNode *head = new ListNode(1);
    ListNode *node1 = new ListNode(2);
    ListNode *node2 = new ListNode(3);
    ListNode *node3 = new ListNode(4);
    head->next = node1;
    node1->next = node2;
    node2->next = node3;
    node3->next = node1;
    
    Solution solution;
    ListNode *rNode = solution.detectCycle(head);
    if(rNode)
        cout<<rNode->val<<endl;
    
    return 0;
}