Destroy Transportation system
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 900 Accepted Submission(s):
465
Problem Description
Tom is a commander, his task is destroying his enemy’s
transportation system.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
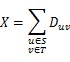
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
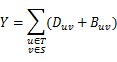
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
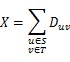
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
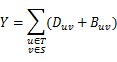
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Input
There are multiply test cases.
The first line contains an integer T(T<=200), indicates the number of cases.
For each test case, the first line has two numbers n and m.
Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)
The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.
The first line contains an integer T(T<=200), indicates the number of cases.
For each test case, the first line has two numbers n and m.
Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)
The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.
Output
For each case, output "Case #X: " first, X is the case
number starting from 1.If such set doesn’t exist, print “happy”, else print
“unhappy”.
Sample Input
2
3 3
1 2 2 2
2 3 2 2
3 1 2 2
3 3
1 2 10 2
2 3 2 2
3 1 2 2
Sample Output
Case #1: happy
Case #2: unhappy
析: 有一个n个顶点m条边的有向图, 每条边有两个权值d, b表示拆掉该边花费以及将该边重建为无向边的花费, 要求从该图中任意选取一个子图S, 其补图为T,
X为拆掉边uv(u属于S, v属于T)的总花费, Y为拆掉边uv(u属于T, v属于S)以及重建该边的花费, 问是否任意都有X <= Y
看 X <= Y 的情况:
由于改图为强连通图, 每个点都有出边和入边, 出边加X的值, 入边加Y的值, 要是满足 X == Y 则肯定满足 X <= Y, 现在要使 X == Y , 即要求每个点的入流等于出流, 即求无源汇有上下界的网络流是否存在可行流
1.构建一个虚拟源点与汇点
2.计算每一个点的D[i] = 该点所有入流 - 观点所有出流
3.判断:
如果D[i] > 0, 累加D[i], 并在源点与该点之间建有向边
如果D[i] <= 0, 在该点与汇点之间建有向边
4.计算最大流

#include <queue> #include <math.h> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> #include <functional> #define ll long long #define ull unsigned ll #define Inf 0x7fffffff #define maxn 50005 #define maxm 100005 #define P pair<int, int> #define eps 1e-6 #define mod 10000 using namespace std; const int N = 205; int t, n, m, len, ans; int u, v, d, b, S, T; int D[N], h[N], dis[N]; struct Node{ int v, w, nxt; }g[maxn]; void init(){ ans = 0; S = 0, T = n+1; fill(h, h+N, -1); fill(D, D+N, 0); } void add(int u, int v, int w){ g[ans].v = v; g[ans].w = w; g[ans].nxt = h[u]; h[u] = ans++; } bool bfs(){ fill(dis, dis+N, -1); queue<int>Q; Q.push(S); dis[S] = 0; while(!Q.empty()){ int u = Q.front(); Q.pop(); for(int i = h[u]; i+1; i = g[i].nxt){ int v = g[i].v; int w = g[i].w; if(w > 0 && !(dis[v]+1)){ dis[v] = dis[u]+1; Q.push(v); } } } return dis[T]+1; } int dfs(int u, int flow){ int cost = 0; if(u == T || !flow) return flow; for(int i = h[u]; i+1; i = g[i].nxt){ int v = g[i].v; int w = g[i].w; if(w > 0 && dis[v] == dis[u]+1){ int f = dfs(v, min(w, flow-cost)); if(f > 0){ g[i].w -= f; g[i^1].w += f; cost += f; if(cost == flow) //剪枝 break; } } } return cost; } int dinic(){ int f, flow = 0; while(bfs()){ while((f = dfs(S, Inf)) > 0){ flow += f; } } return flow; } int main(){ int tot = 1; scanf("%d", &t); while(t--){ scanf("%d%d", &n, &m); init(); for(int i = 0; i < m; i ++){ scanf("%d%d%d%d", &u, &v, &d, &b); add(u, v, b); add(v, u, 0); D[u] -= d; D[v] += d; } int flow = 0; for(int i = 1; i <= n; i ++){ if(D[i] > 0){ flow += D[i]; add(S, i, D[i]); add(i, S, 0); }else{ add(i, T, -D[i]); add(T, i, 0); } } if(flow == dinic()) printf("Case #%d: happy ", tot++); else printf("Case #%d: unhappy ", tot++); } return 0; }
