算一个数组的所有组合方式

目的：给一个数字数组，算出这个数组的所有组合方式。

例子：比如给一个数组为{23，44，56}（这里为了能列举出所有的组合方式，所以选择一个长度较小的数组），那么我们所要得到的结果为6组数：{23，44，56}，{23，56，44}，{44，23，56}，{44，56，23}，{56，23，44}，{56，44，23}。这三个数所能组成的数组方式不会再有第七种。

不考虑的问题：本文没有考虑类似这样的情况：给定的数组中的数有同值，比 如，{23，23，56}，从而得到的组合方式除去冗余数据后，并没有6组。

关键词：

数组：本文指一个长度至少为1的数字数组对象。如{11，22，44}。

数组元素：文本指数组中的单个数值，如{11，22，44}中有三个数组元素分别为：11，22，44

数组长度：本文指一个数组中数组元素的个数。

组合方式：本文指数组元素在本数组中出现的顺序。

基本算法思想：

如果数组的长度为1如下：

11

那么，返回的数组的组合方式自然是一种，其值为11。

但是我在此基础上加了一个数，长度为2，如下：

11

22

那么，返回的数组是两个组合方式，如下：

11	22
22	11

以此类推，如果我再加入一个元素，使数组长度为3，那么所能组合成的数组也就如同前文提到的6个：

11	22	33
11	33	22
22	11	33
22	33	11
33	11	22
33	22	11

那么下面就可以说规律性的东西了。

当数组长度为1时，返回的组合方式只有1种，就是它本身。当新加一个数组元素时，这个新元素就会与原来的每一种组合方式中的每个数组元素发成关系，表现为：新数组元素在原来的每一种组合方式中的 各个位置分别插入一次，这样就出现更多的组合方式，而这所有的组合方式的合集，就是加入新元素后的新数组的所有组合方式，如图：

11

这个数组只有一个数组元素，我们然后新添加一个数组元素，值 为22，那么：

22

11

22插入到11之前

11

22

22插入到11之后。那么{22，11}、{11，22}就是加入了22这个新数组元素后的所有组合方式了。

如果再加入新组数元素33，那么：

33	22	11
22	33	11
22	11	33
33	11	22
11	33	22
11	22	33

前三行分别是把新数组元素33插入到上文所得到的第一个组合方式{22，11}中，后三行分别是把新数组元素33插入到上文所得到的第二个组合方式{11，22}中。形成的组合方式就是上图所画的6种组合方式，而它也是数组{11，22，33}的所有组合方式了。

实现：实现这个算法，那么免不了要用到递归了。下面先看一下递归 的示例图：

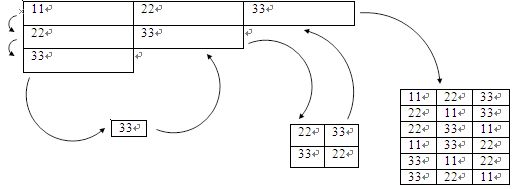
代码：

 public static List<int[]> GetDataArray(int[] data)
        {        
            List<int[]> list = new List<int[]> ();            
            if(data ==null)
                return list;
            if (data.Length == 1)       //如果长度为1，那么返回它的组合方式，即它本身。
            {           
                list.Add(data);                
            }
            else  //否则，引入新的数组元素，并插入到原有的组合方式的各个位置，形成新的组合方式。
            {
                int[] dataSub = new int[data.Length - 1];
                for (int i = 0; i < data.Length - 1; i++)
                {
                    dataSub[i] = data[i + 1];
                }
                List<int[]> listOld = GetDataArray(dataSub);  //获取原有的组合方式
                
                
                int newNum = data[0];
                int[] newData = null;
                for (int i = 0; i < listOld.Count; i++)           //遍历每一种原有的组合方式
                {
                    for (int j = 0; j <= listOld[i].Length; j++)  //遍历组合方式中的每个位置
                    {
                        newData = new int[listOld[i].Length + 1];
                        newData[j] = newNum;
                        int currentIndex = 0;
                        for (int n = 0; n < listOld[i].Length; n++)
                        {
                            if (currentIndex == j)
                                currentIndex++;
                            newData[currentIndex] = listOld[i][n];
                            currentIndex++;

                        }
                        list.Add(newData);
                    }
                }
                
            }
            return list;

        }