TD是一个结合DP和MC之间的方法。TD不需要环境模型,但是又可以bootstrap。
6.1 TD预测
典型的TD(0)预测方程:
![]()
看第三章关于状态价值的等式:
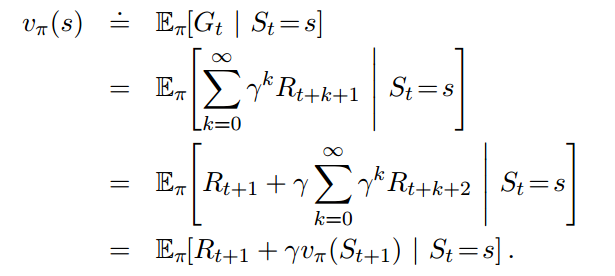
MC用的是第一行,它之所以为估计,因为不知道$G_t$的期望值,而使用的采样来做的平均。
DP用的是最后一行,它之所以为估计,是因为不知道$v_{pi}(S_{t+1})$,是通过迭代方式不断更新的。
而TD则是两者的结合,它通过采样来获得$R_{t+1}$,通过迭代来获取$v_{pi}(S_{t+1})$

6.2 TD方法的优点
相对于DP,TD不需要模型,相对于MC,TD是一种在线算法。同时TD通常比MC收敛更快。

6.3 TD(0)的最优化
MC收敛到最小均方
TD收敛到马尔科夫过程的最大似然,但是TD接近最小均方的效率也比MC要好。
6.4 Sarsa:On-Policy TD控制
我们这是使用action value
![]()

6.5 Q学习:Off-Policy TD控制
把上面的式子作修改:
![]()

之所以称为off-policy,是因为红框处的a的选取是根据最大值,而不是由当前策略决定的。
6.6 期望Sarsa
我们对Sarsa的迭代式作另外一种修改:
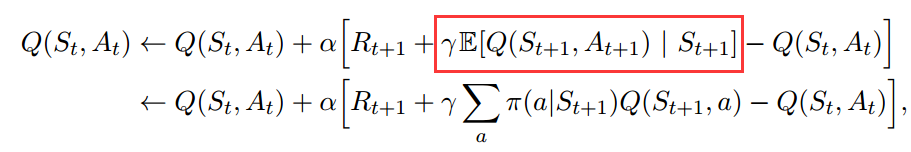
三者在Cliff Walking问题上的表现差异:
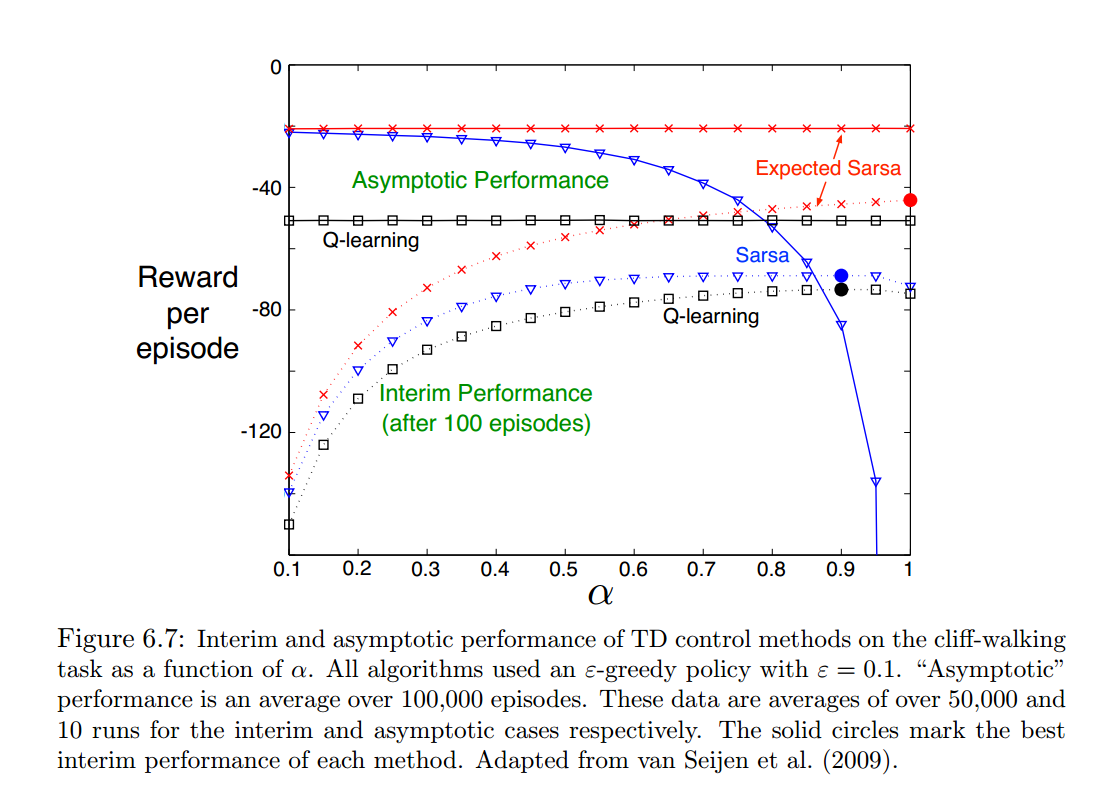
Expected Sarsa也是一种在线算法,因为它是根据当前策略来定的下一个A,只是做了平均。当然也可以修改成一个off-line的算法,例如用一对policy的方式。
三种方法非常类似,唯一区别就是在估算过程中选择下一个action的方式。
6.7 最大化偏差和成对学习
上面三种方法都存在最大化偏差问题:

![]()
根据上面这个式子,对初始点$S_t=A$来说,当$A_t=left$时,红框中的数值通常大于零。但是实际上均值是-0.1。对Sarsa,Expected Sarsa也是如此。
观察上面的曲线,一开始会偏差很远,之后渐进到最佳值,依然还是有偏差。
这个问题并不会导致算法失败,但是会导致收敛较慢较差。
造成问题的原因是:我们用了同一个序列来做选择动作和评估,解决问题的方法使用:double Q-learning,建立两个Q函数。
![]()

6.8 案例(略)