我们通过参数θ定义偏好函数$h(s,a, heta)$,通过h的softmax表示$pi(a|s)$,然后根据$pi(a,s)$计算优劣度$eta( heta)=v_{pi_{ heta}}(s_0)$,最后,通过计算$eta$对$ heta$的梯度,来实现$ heta$的更新。
13.1 策略梯度定理
定义策略优劣度:$eta( heta)=v_{pi_{ heta}}(s_0)$
可以证明:
![]()

注意上面证明过程中$d_{pi}(s)=displaystylesum_{k=0}^{infty}gamma^k Pr(s_0 o s,k,pi)$,表示按照策略π从起始状态$s_0$到达状态s的总可能性,并且根据步数作了折扣。这个值非常地不直观,也不利于下面的推导。因此我不用d这个变量。
13.3 MC的策略梯度方法
书中推导过程有些晦涩,这里我用更直观的方式来表达:
$ ablaeta( heta)=displaystylesum_ssum_{k=0}^{infty}gamma^k Pr(s_0 o s,k|pi)sum_a ablapi(a|s)q_{pi}(s,a)$
$=displaystylesum_ssum_{k=0}^{infty}sum_a Pr(s_0 o s,k|pi)pi(a|s)frac{ ablapi(a|s)}{pi(a|s)}gamma^k q_{pi}(s,a)$
$=displaystylesum_ssum_{k=0}^{infty}sum_a Pr(s_0 o s,a,k|pi)pi(a|s)frac{ ablapi(a|s)}{pi(a|s)}gamma^k q_{pi}(s,a)$
其中$Pr(s_0 o s,a,k|pi)$表示在策略π下,k步达到s且采取a的概率。
而$G_k$恰好是$q(s,a)$的采样,表示从k往后平均能获得多少总奖励
$=E_{pi}[frac{ ablapi(a|s)}{pi(a|s)}gamma^k G_k]$ (这里表达不严格,因为k是积分变量)
梯度算出来之后,就有了迭代更新式(梯度上升):
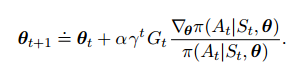

对线性模型+softmax的偏好函数来说,我们有:
![]()
13.4 基线
为了减少学习的方差,我们引入基线函数$b(s)$
![]()
$b(s)$可以取任何值,任何函数,只要不和a相关,就不影响上面式子的结果。因为:
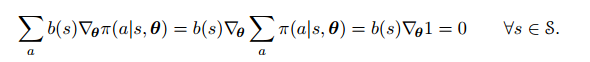
但是,对于随机梯度下降来说,因为我们是根据一个一个取样来实现梯度上升,引入基函数可以极大地减少更新时的波动。更精确地,当
$b(s)=E_a[q_{pi}(s,a)]=v(s)$时,方差将最小。
因此,我们在改进η的同时,我们也要设法计算$v(s)$,因此我们引入一个新的参数w来计算$v(s)$
θ的迭代更新式为:
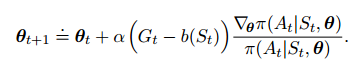

13.5 Actor-Critic方法
上面使用MC方法,为了改善学习性能,我们介绍TD方法。这时候,value函数不仅用来当baseline,还要用来backup。下面是TD(0)的迭代更新式:
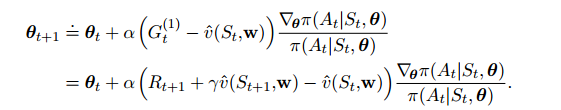

结合前一章资格迹,TD(λ)的算法如下:

13.6 连续问题的策略梯度方法
连续问题中,η定义为每一步的平均收益:
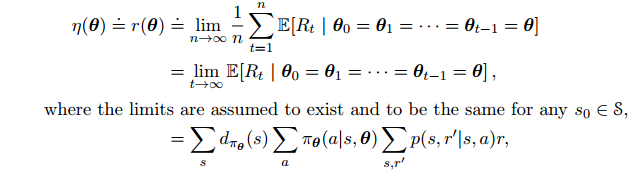
其中$d_{pi}(s)$为状态$s$出现的比例
![]()