来自:【数据结构与算法分析——C语言描述】练习2.7
问题描述:假设需要生成前N个自然数的一个随机置换。例如,{4,1,2,5,2} 和 {3,1,4,2,5} 就是合法的置换,但 {5,4,1,2,1} 却不是,因为数1出现了两次而数 3 缺没有。这个程序常常用于模拟一些算法。我们假设存在一个随机数生成器 randInt(i, j) ,它以相同的概率生成 i 和 j 之间的一个整数。
下面是三个算法:
1.如下填入 A[0] 到 A[N-1] 的数组 A;为了填入 A[i] ,生成随机数直到它不同于已经生成的 A[0], A[1], ... , A[i-1] 时,再将其填入 A[i] 。
2.同算法1,但是要保存一个附加的数组,称之为 Used(用过的)数组。当一个随机数 Ran 最初被放入数组A的时候,置Used[Ran]=1。这就是说,当用一个随机数填入 A[i] 时,可以用一步来测试是否该随机数已经被使用,而不是像第一个算法那样(可能)进行 i 步测试。
3.填写该数组使得 A[i] = i + 1。然后
for(i = 1; i < N; i++)
swap(&A[i], &A[randInt(0, i)]);
题目中有说“我们假设存在一个随机数RandInt(i, j)”,既然如此,暂时不必考虑其内部实现以及内存限制,只根据这个接口考虑算法即可。
算法1
i = 0;
while (i < N)
{
ran = randInt(0, N);
for (k = 0; k < i; k++)
{
if (A[k] == ran)
break;
}
if (k == i)
{
A[i] = ran;
count++;
}
}
以循环次数作为时间度量。循环从i=0到i=n-1写出n个不重复随机数,因为生成第i个不重复随机数的概率是(N-i)/N,所以理论上经过N/(N-i)次生成,得到不重复随机数的概率为1。所以总耗时为
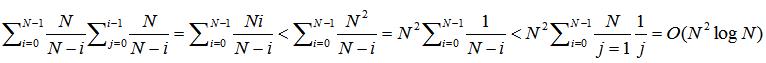
这里做了分子的放大,以及这个调和和公式: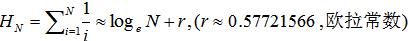
该算法的时间复杂度即为O(N2logN)。
算法2
i = 0;
while (i < N)
{
ran = randInt(0, N);
if (used[ran] == 0)
{
A[i] = ran;
used[ran] = 1;
i++;
}
}
算法 2 比算法 1 少了内层的 for 循环,所以时间复杂度降了一阶,即为 O(NlogN)。
算法3
for (i = 0; i < N; i++)
A[i] = i + 1;
for (i = 0; i < N; i++)
swap(&A[i], &A[randInt(0, i)]);
时间复杂度显然是线性级的,O(N)。