前言
机器学习主要分为两大类别:
- 有监督学习(Supervised Learning)
- 无监督学习(Unsupervised Learning)
- 其他:强化学习(Reinforcement)、推荐系统(Recommender systems)
有监督学习
有监督学习的特点:在监督学习中,数据集中的每个样本均给出了对应的结果,我们设法利用样本进行预测目标输出即可。
有监督学习包括回归问题(Regression)与分类问题(Classification)。
- 回归问题:预测一个连续值输出,算法的目的是根据有限的离散数据(样本)得到连续输出。
如:利用离散样本(房子面积、房子价格)预测任意面积的房子价格。 - 分类问题:推断离散的输出值,用于进行分类的特征有多个。
如:给算法输入一张图像,判定图像是属于狗还是属于猫两个类别。
无监督学习
无监督学习的特点:数据集样本并未给出结果/标签,只给算法输入了一堆数据,让算法自己去分标签。
如:
- Google News对大量的新闻分簇,最后归类显示不同主题的新闻;
- DNA微阵列数据等;
- 根据网络社交数据分析不同的社交圈;
- 根据大量的客户数据分析得到不同的细分市场;
- 聚类算法用于分析天文学、星系的形成过程等;
一元线性回归
线性回归模型
Univariate(一元、单变量) linear regression
样本数据格式为【房子价格、房子面积】,一共有m个样本,利用机器学习建立模型,给模型输入房子面积,模型返回房子价格。
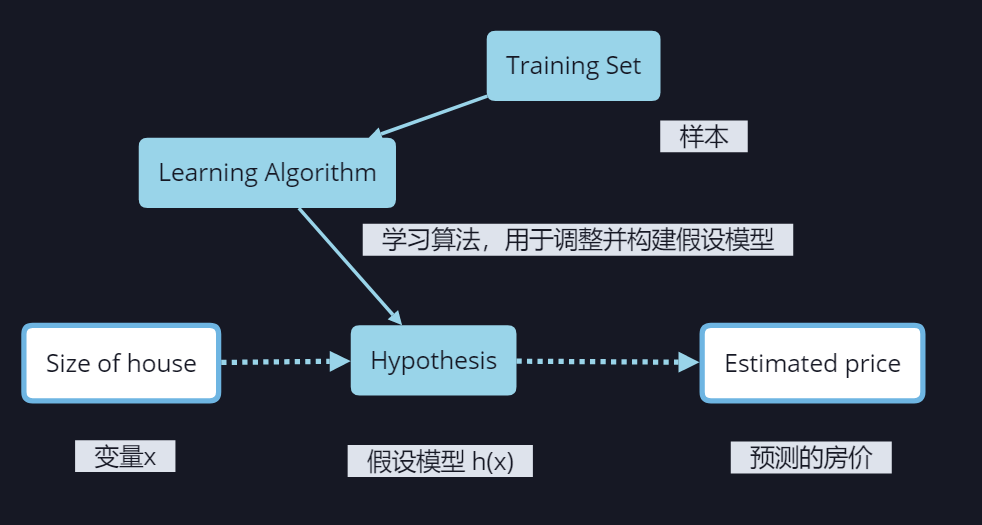
将这m个离散样本(假设是7个)表示在图像上,如下图所示:

题设其实就是一元线性回归,利用一元线性回归会比较容易理解什么是线性回归,所谓一元线性回归,就是利用一条直线去对离散样本值进行拟合,通过这条直线可以获得任意特征值下的预测值。对于多元线性回归也是同样的道理。图中假设的拟合直线(Hypothesis)如下。
可以看出这个假设的公式会随着θ0和θ1的值进行变化,那么如果想要得到一条最佳的拟合直线,就需要求出最小代价J(θ)时θ0和θ1的值。这就是应当去解决最小化问题。
代价函数
Cost Function
代价函数又被称为平方误差函数,代表着离散样本与拟合直线的平方误差。可以想象,代价函数的值随着θ0和θ1改变而改变,当代价函数J(θ0,θ1)处于最小值的情况时,此时的θ0和θ1便是最优的模型参数。
到这里暂时总结下,现在已经知道了假设模型、模型参数以及代价函数,现在的目标就是求解代价函数的最小值。
- Hypothesis假设函数
- Parameters模型参数
- Cost Function代价函数
- Goal目标
假设θ0=0,那么h(x)=θ1x,J(θ)的大小也只与θ1有关,J(θ)取值随着θ1的变化图像如下:
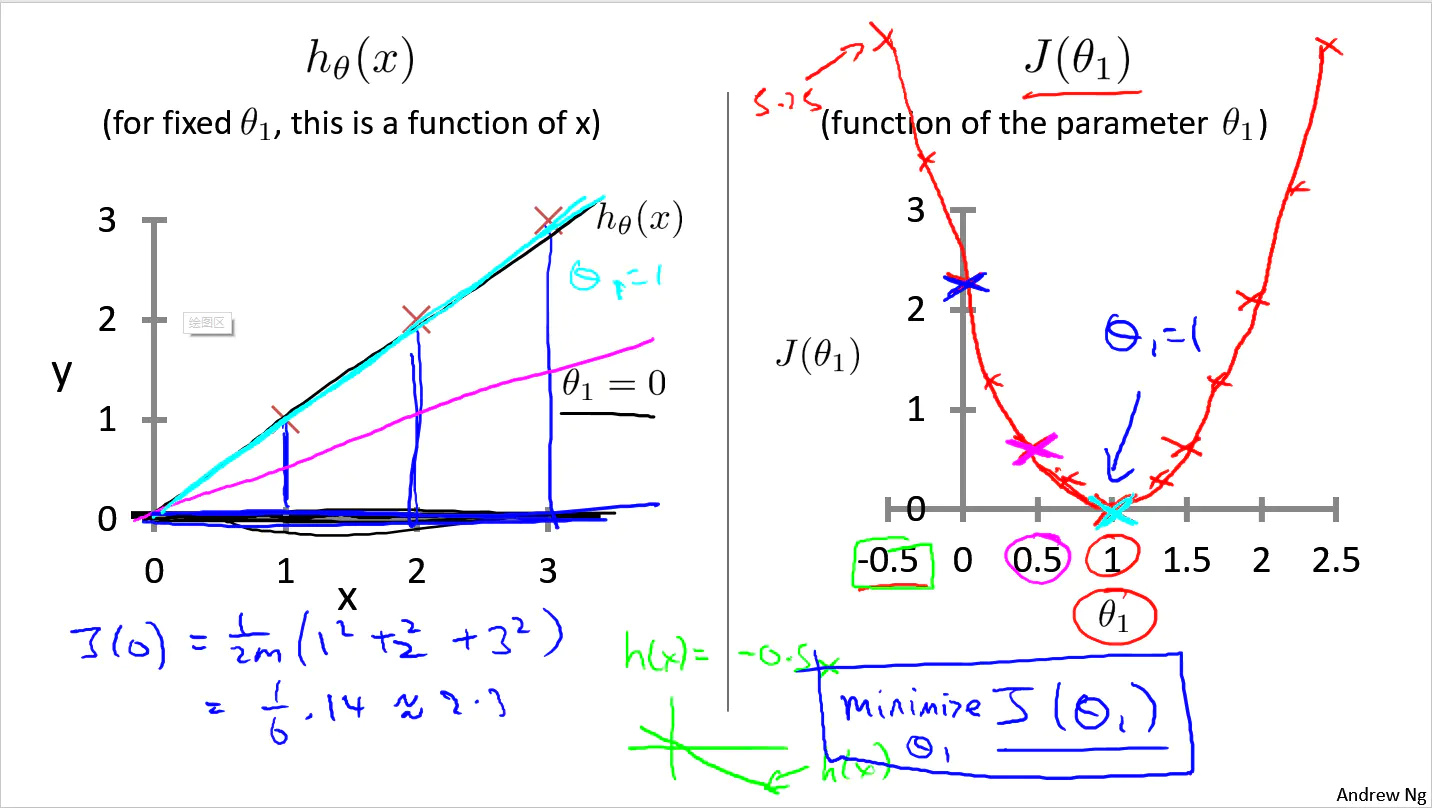
当θ0与θ1均可以任意变化时,代价函数J的大小取决于θ0和θ1的共同作用,函数图像如下:

每次更改θ0和θ1值的时候,J(θ0,θ1)的值都不同,如果想要得到J(θ0,θ1)的最小值,我们显然不可以手动的一个个去测验哪一对(θ0,θ1)是最优解,这个时候解决问题最好的方法就是设计一个能够自动寻找代价函数J(θ0,θ1)最小值时参数(θ0,θ1)的算法。
梯度下降
Gradient descent algorithm
repeat until convergence:(for j=0 and j=1)
- 这里为了简化只考虑了假设模型只有θ0,θ1两种。需要注意的是各参数一定要同步更新(Simultaneous update)

- α表示的是学习率(learning rate),α用来控制在梯度下降的过程中迈出多大的步子,当α很大的时候就会快速的下降(有可能直接越过收敛区域),当α很小的时候就会特别慢才能达到收敛区域。α右侧是一个偏导项,具体的作用主要是为梯度下降提供下降方向和控制下降步伐(某种程度上这样理解应该没问题吧)。当代价函数越来越接近最优解的时候,偏导项的值会越来越小,那么梯度下降的步伐会越来越小,直到收敛的时候梯度下降不会再更改模型参数。

- 梯度下降会因为模型参数初始化的不同而获得不同的局部最优解。需要注意的是:线性回归的代价函数永远是一个凸函数(弓形函数Bowl-shaped),没有局部最优解,只有全局最优解。也就是说在线性回归的模型中使用梯度下降法所得到的最优解是唯一的,但是在其它模型中就未必了,下图解释了什么是局部最优。
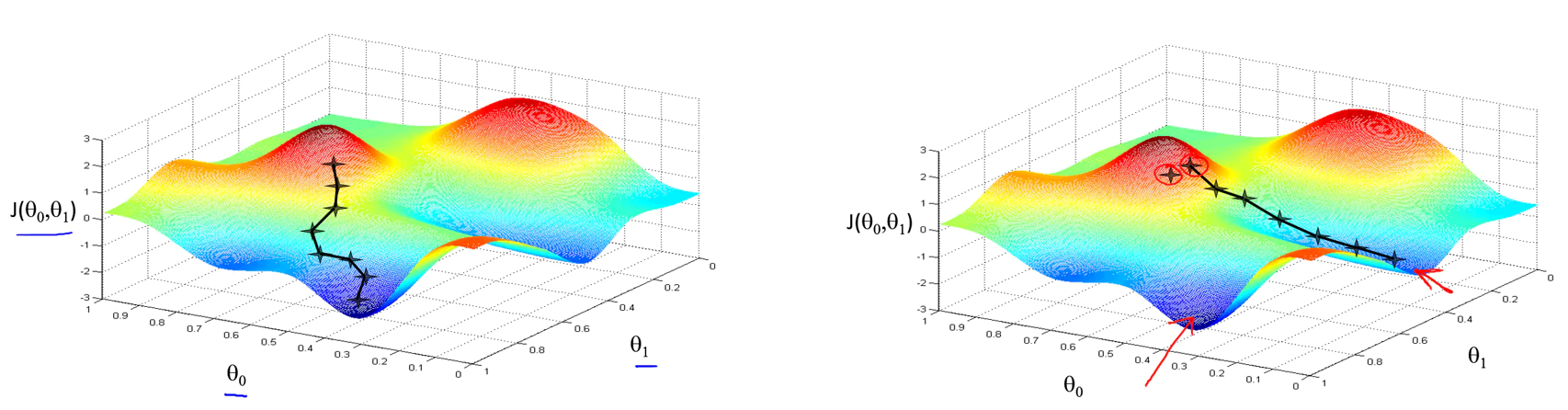
化简梯度下降
将梯度下降算法与线性回归模型结合
- j=0时(θ0):
- j=1时(θ1):
解释一下这里的i是什么,i代表着样本的索引

多元线性回归
Linear regression with multiple variables
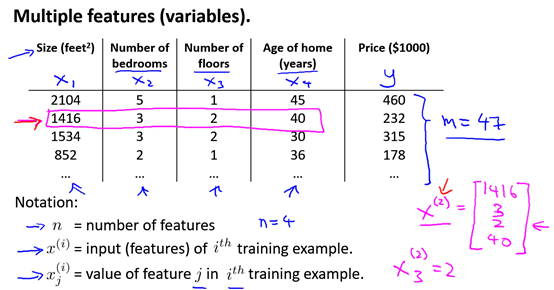
- 用n表示特征值的个数,m表示样本的个数。
- x(i)表示的是样本的索引,xj表示的是特征的索引。
- 在矩阵的索引中,除非特殊指定,一般都是从1开始进行索引。如果要具体的应用到机器学习中就应当从0开始索引。

多元线性回归相关的公式如下:
- Hypothesis假设函数
注:为了方便矩阵运算(见上图),将x0定义为1。
- Parameters模型参数
- Cost Function代价函数
- Gradient descent梯度下降
repeat until convergence:
特征缩放
Feature Scaling

在没有进行特征缩放之前,运行梯度下降的过程可能会花费很长的一段时间,事实上上述椭圆等高线会更加的瘦长,因此在进入到最优位置时会花费更久的时间。由于路线足够长,梯度下降的过程也可能会来回的波动。
特征缩放过程中一般缩放在-11即可,最大的范围可以是-33,超过这个范围一般需要进行缩放,这样才能够保证梯度下降正常工作。
均值归一化
Mean normalization

- 用xi-ui替代xi,目的是确保处理后的特征值大约具有一个为0的均值 - 不要对x0进行均值归一化,xi被定义成为1,是不可改变的。 - ui代表的是特征值的平均值。
α的选择
Learning rate
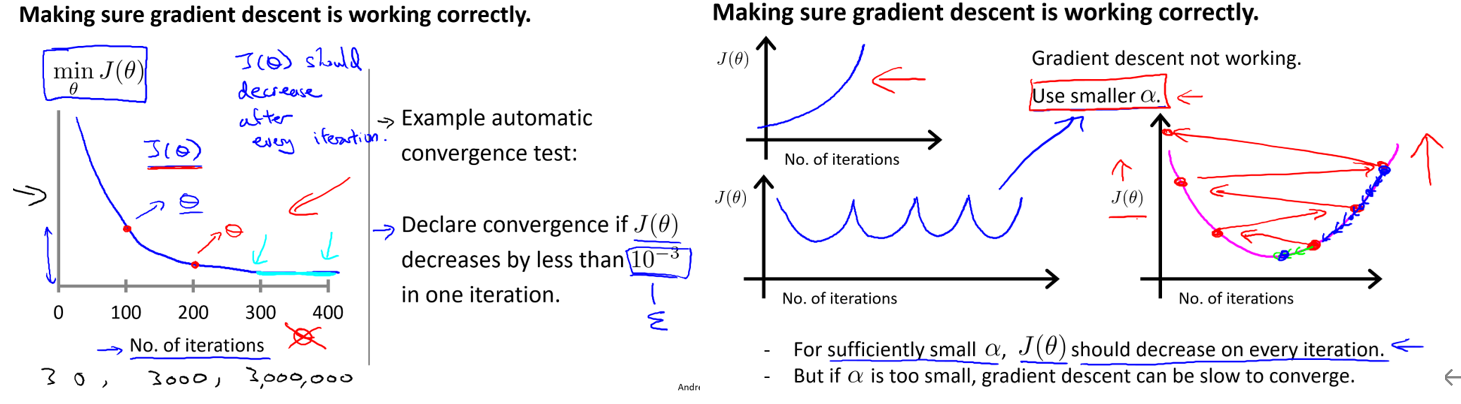
如果学习率太小,那么收敛的特别慢,如果学习率过大,那么代价曲线会上升或者波动。
一般在选择学习率的时候可以3倍3倍的进行选择,如0.001、0.003、0.01、0.03、0.1、0.3、1.0等。
多项式回归
Polynomial regression
特征处理
假设样本给出了房子的长度和宽度,以及房价,那么具体利用深度学习的时候可以好好的考虑下对房子长度和宽度的利用,房子长宽肯定不是衡量房价的最好特征,可以使用房子面积(长×宽)来进行衡量,这种情况下问题就简单很多了。有的时候通过定义新的特征,可能会得到一个更好的模型。
拟合非线性函数

多项式回归:可以利用线性回归的方法拟合一些非常复杂的函数,甚至非线性函数。在这里需要注意的是,多项式回归模型仍然是建立在多元线性回归的基础上的,一定不能忘记特征缩放的过程,否则梯度下降很可能不会工作。除了选择上图左侧的三次函数模型,也可以使用右侧的幂函数,这个要看样本分布的图像来进行具体的设计。
正规方程
Normal equation
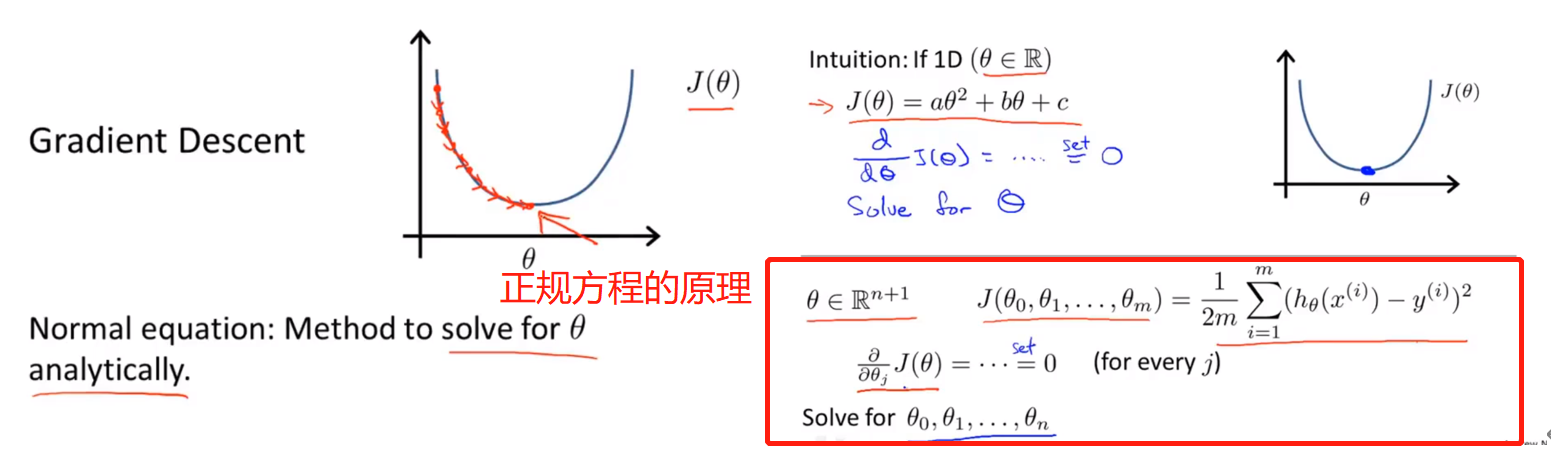
正规方程是一个使用线性代数知识直接对模型参数进行计算的方法,也就是直接对梯度下降偏导项等于0进行求解。

- 正规方程如下:
- 正规方程“=”右侧,y左侧的部分化简之后刚好为X的逆
- 这里的0其实就是一个由模型参数构成的列向量
- 使用Octave的pinv可以求得伪逆
- 当XTX不可逆的时候,一般有两种情况,其一是有线性相关(冗余)的特征,其二是特征远大于样本。对于第一种情况来说可以删除线性相关的部分特征,对于第二种情况来讲可以删除一些特征或者使用正则化(regularization)删除。
pinv(X'*X)*X'*y
- 如果使用正规方程去求解0的值,就不需要使用特征缩放。
正规方程 VS 梯度下降
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 α | 不需要 |
| 需要多次迭代 | 一次运算即可 |
| 特征数量n很大的时候仍可以使用 | n>10000时速度变慢 |
| 适用于各种类型的模型 | 只适合线性回归模型 |