《极客时间--算法面试》--递归和分治

目录

　　递归

　　分治

1、求指数

n的阶乘的计算法方式。

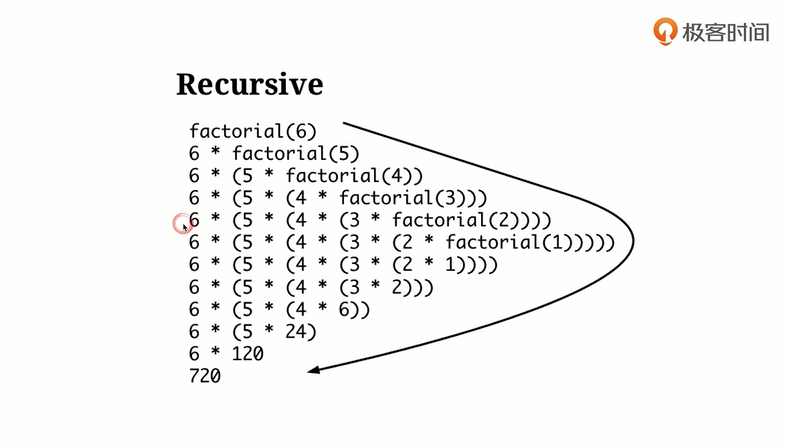
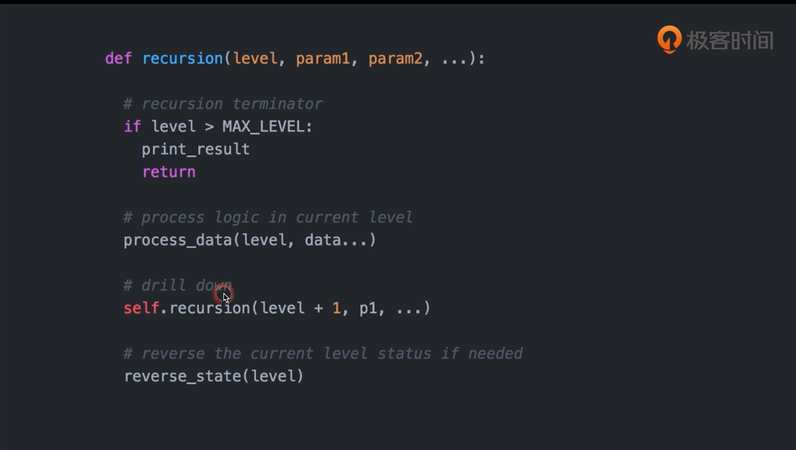
递归的必要条件

　　参数里面有明显的层级，level。

　　递归的终止条件。大多数在最前面

　　数据的处理

　　调用下一层

　　解决完下一层的任务后做的工作（按需）

 分治

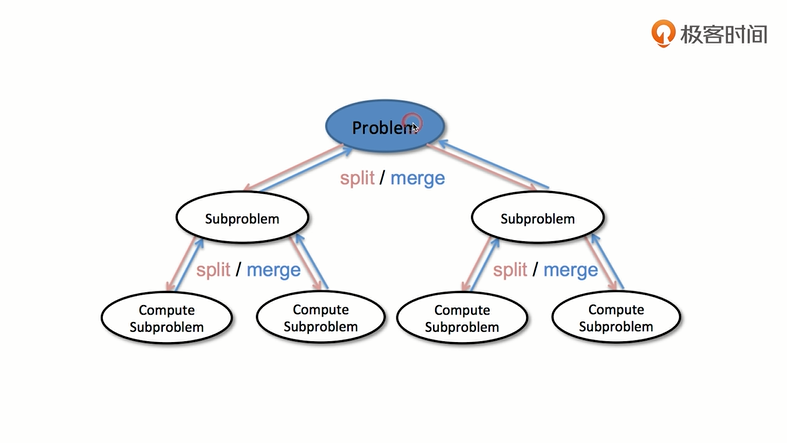
分治思路：

　　明确问题problem

　　明确终止条件

　　准备数据并将大问题拆分成小问题

　　对子问题进行解决

　　对子结果进行合并

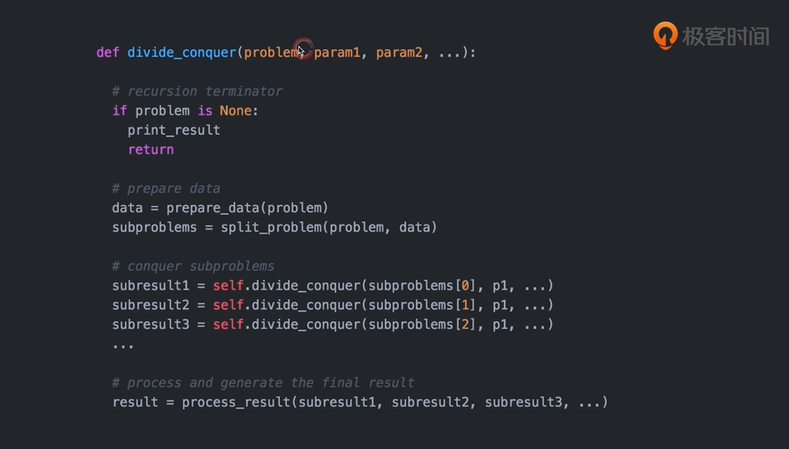
 Pow（x,n）

https://leetcode-cn.com/problems/powx-n/submissions/

思路：

　　一、如果采用循环遍历的话，将是O(n)时间复杂度

　　二、如果采用分治思想的话将是logn时间复杂度

代码：

class Solution(object):
    def myPow(self, x, n):
        """
        :type x: float
        :type n: int
        :rtype: float
        """
        if n<0:                         #如果是负数幂
            x = 1/x                     #结果是倒数
            n = -n                      #将n转为正数
        Pow = 1                         #累计结果值
        while n:                        #循环遍历
            if n&1:     
                Pow *= x                #如果是奇数的话就会多乘一次
            x *= x                      #x自身累乘
            n = n>>1                    #右移是除以2
        return Pow                      #最终返回结果值

众数

https://leetcode-cn.com/problems/majority-element/submissions/

思路：

　　一、采用暴力进行求解，时间复杂度为n平方

　　二、采用集合统计次数，世间复杂度为O(n)

　　三、采用排序的方式，平均下快排是最快的nlogn时间复杂度

　　四、分治的思想

代码：

class Solution(object):
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
                                        #这个代码和下面的思路一样，更多采用了集合进行缓存
        dic = {}
        for item in nums:
            if item not in dic:
                dic[item] = 1
            else:
                dic[item] += 1
        value = 0
        for item in dic:
            if dic[item] >value:
                key = item
                value = dic[item]
        if value>len(nums)/2:
            return key
        """
        for item in set(nums):                  #遍历元素，set是去重复
            if nums.count(item)>len(nums)/2:    #对元素个数进行技术，符合条件
                return item                     #返回元素值