(S) 3.3 闭区间上连续函数的基本性质
定理3.3.1:有界性
设 (f(x)in C[a,b]) 则 (f(x)) 在 ([a,b]) 上有界。也就是像下图说的那样
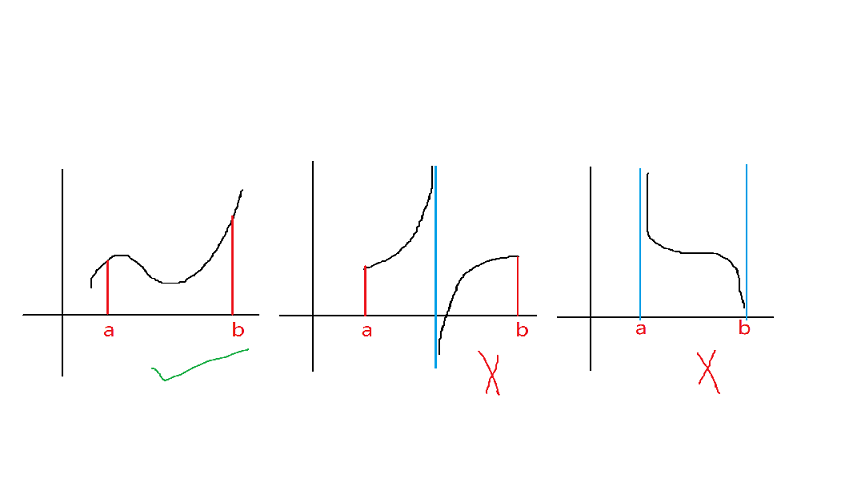
补充:无穷大于无界的关系
简单的说无穷大就是是当 (x) 趋于某一值时函数值必须单调地趋于无穷大,无界就是当 (x) 趋于某一值时函数值不单调地或者单调地趋于无穷大,至于发散就是不收敛。
证明1:
方法很多,这里的第一种方法使用 (Bolzano-Weierstrass) 定理和 (Henie) 定理
证1:(反证法)
假设 (f(x)) 在 ([a,b]) 上连续,但是无界. 则根据无界的定义[forall \, M>0, exists\,x_0 in [a,b], extrm{使得}; |f(x)|>M ]无界可以联想到无穷大,但必须取离散的点作为自变量才能保证无穷大。由无穷大可以找矛盾点:在这些离散点的定义下存在极限等于实数。可以考虑 (Bolzano) ,然后因为在函数下讨论序列问题,可以考虑用 (Henie) 。
则取 (M) 等于 (1,2,cdots,n) ,有
[1>0,exists\,x_1in[a,b], |f(x)|>1\ 2>0,exists\,x_2in[a,b], |f(x)|>2\ vdots\ n>0,exists\,x_nin[a,b], |f(x)|>n\ ]从而有 (mathop{lim}limits_{n o infty}f(x_n)=infty)
现在我们得到了一个数列 ({x_n}) ,它不一定收敛,但它有界,则有 (Bolzano) 定理可得它一定有收敛子列,不妨记作 ({x_{n_k}}) ,收敛于 (x_0)
加之 (f(x)) 在 ([a,b]) 上连续(闭区间,则极限一定能够等于当前点的函数值),结合 (Henie) 定理,(mathop{lim}limits_{k o infty}x_{n_k}=x_0 Longrightarrowmathop{lim}limits_{k oinfty}f(x_{n_k})=f(x_0))
如果一个数列收敛于一个数或者无穷,那么它的子列也收敛到同一个数或无穷。此处就产生了矛盾。
证毕
证明2
闭区间套
证2:(反证法)
假设 (f(x)) 在 ([a,b]) 上连续,但是无界,则对于区间 ([a,frac{a+b}{2}]) 和 ([frac{a+b}{2},b]) ,(f(x)) 一定在其中的某个区间内无界。令这个子区间为 ([a_1,b_1]) 则对于 ([a_1,frac{a_1+b_1}{2}]) 和 ([frac{a_1+b_1}{2},b_1]) ,(f(x)) 一定在其中的某个区间内无界。
如此下去,则可以得到一个闭区间列 ({[a_n,b_n]}) 满足:
(1. a_{n-1}le a_n<b_nle b_{n-1})(2. mathop{lim}limits_{n oinfty}b_n-a_n=0)
(3. f(x)) 在每个区间上无界
则由闭区间套定理,(exists!\,cin[a_n,b_n],forall ninmathbb{N}) .
由条件 (2) 知 (exists n>0) 使得 ([a_n,b_n] subset U(c,delta)) 即 (f(x)) 无界。由连续函数的局部有界性,(exists\, delta>0) ,使得当 (forall xin U(c,delta)) 时,(f(x)) 有界。
这与条件 (3) 矛盾
证毕
定理3.3.2:最值定理
设 (f(x) in C[a,b]) ,则 (f(x)) 在 ([a,b]) 上必有最小值和最大值。
很好理解,同上图。
证明:
由连续函数的有界性定理,(f(x)) 一定有界。
记 (M=mathop{sup}limits_{xin[a,b]}{f(x)}) , (m=mathop{inf}limits_{xin[a,b]} { f(x) })
由上确界的定义,可得上确界是 (f(x)) 的一个聚点。则存在数列 ({ x_n }) 使得 (mathop{lim}limits_{n oinfty} f(x_n) = M) 。
下面证明存在一个数 (xi) 使得 (f(xi) = M) :设 ({ x_{n_k} }) 是 ({ x_n }) 的子列,因为 ({ x_{n_k} }) 有界,则 ({ x_{n_k} }) 必收敛,设收敛于 (x_0) 。
由 (Henie) 定理: (mathop{lim}limits_{k o infty} f(x_{n_k}) = M)
因为 (f(x)) 连续,所以有 (mathop{lim}limits_{k o infty} f(x_{n_k}) = f(x_0))
故有 (f(x_0) = M) 即可以取到最大值。
同理可证最小值
证毕。
定理3.3.3:介值定理
设 (f(x) in C[a,b]) ,设 (m=mathop{min}limits_{x in [a,b]} { f(x) }) ,(M=mathop{max}limits_{xin [a,b]}{f(x)}) ,则对,(forall \,eta in [m,M]) ,(exists \,xi in [a,b]) 使得 (f(xi)=eta) ,也即 (f([a,b]) = [m,M])
人话:若 (f(x)) 在 ([a,b]) 连续,则在最大最小值之间的任何一个数都至少对应一个 (x)
证明:
证: (m = M) 时,显然成立。
(m e M) 时,(exists \, x_1,x_2 in [a,b], \, f(x_1) = m, \, f(x_2) = M) 。显然当 (eta = m) 或 (M) 时成立。
假设 (x_1 < x_2),当 (eta in (m,M)) 时,定义:(E = { x in [x_1,x_2]: f(x) > eta })
显然 (x_1 otin E) ,故 (x_1) 是 (E) 的下界
显然 (x_2 in E) ,故 (E) 非空
因此 (E) 一定存在下界。
记 (xi = inf\,E) ,则有 (x_1 le xi <x_2)
由连续函数的局部保号性知:(exists \, delta > 0, forall \, x in (x_1,x_1 + delta) ,f(x) <= eta)
设 (x_* in (x_1,x_1 + delta)) 因为 (xi) 是下界,故有 (xi ge x_* > x_1) 因此 (xi) 严格大于 (x_1)下证 (f(xi) = eta) :
由 (E) 的定义,(f(xi) ge eta) 。
若 (f(xi) > eta) 则由 (f(x)) 在 (xi) 处连续可得:(exists \, delta > 0, forall \, x in (xi - delta,xi + delta) cap [a,b],f(x) > eta)
但因为 (xi) 为下界,故对于 (x in (xi - delta,xi),f(x) le eta) ,矛盾
证毕