【做题笔记】CF938C Constructing Tests

Problem

CF938C Constructing Tests

题目大意：

在一个 (n imes n) 的矩阵中填 (0,1)，使得每一个 (m imes m) 的子矩阵中都包含至少一个 (0)，要让 (1) 的个数最多。

现在知道最多有 (x) 个 (1)，问满足条件的 (n,m)，输出任意一个。如果不存在则输出 -1。

有多组数据，数据组数为 (t)。

Solution

首先我们要去观察原问题，要使 (0) 最少，我们自然希望一个 (0) 能覆盖尽量多的矩阵。
我们假设 (n) 无限大，那么一个 (0) 能覆盖的范围如下：

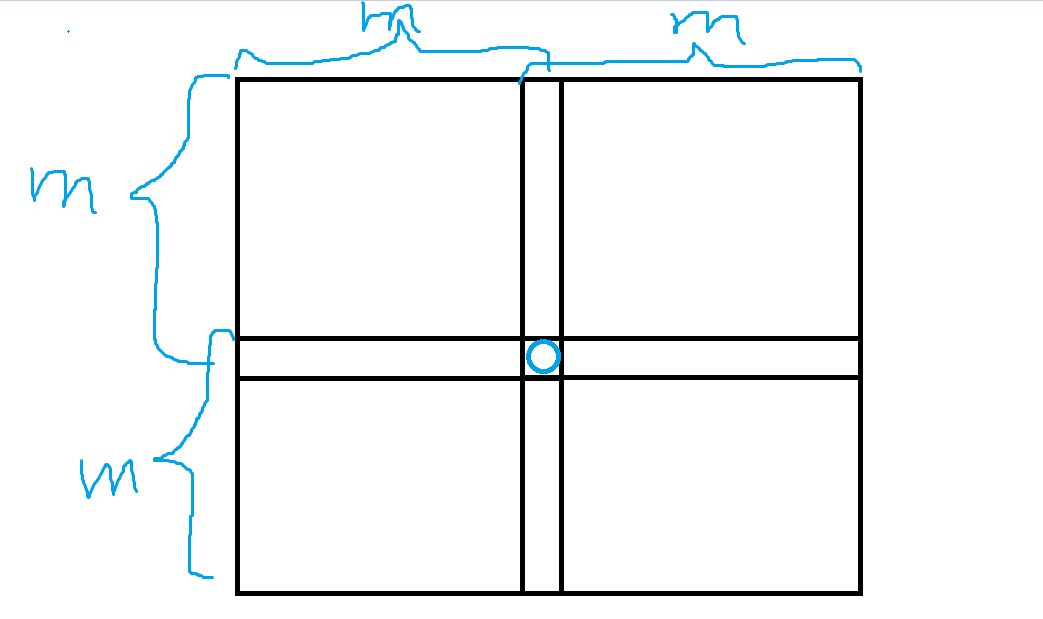
上图中边框内任意一个 (m imes m) 的子矩阵都会包含中间的 (0)。
如果右上角的矩阵再往右移一位，或者左下角的矩阵再往下移一位，就又需要一个新的 (0)，所以我们可以把问题转化成在一个 (n imes n) 的矩形内放置若干 (m imes m) 的矩形，使他们相邻且互不重叠，能放多少个矩形。容易得到答案为 (lfloor dfrac{n}{m} floor ^2)。

这里顺便解释下为什么是下取整。其实看一张图就明白：

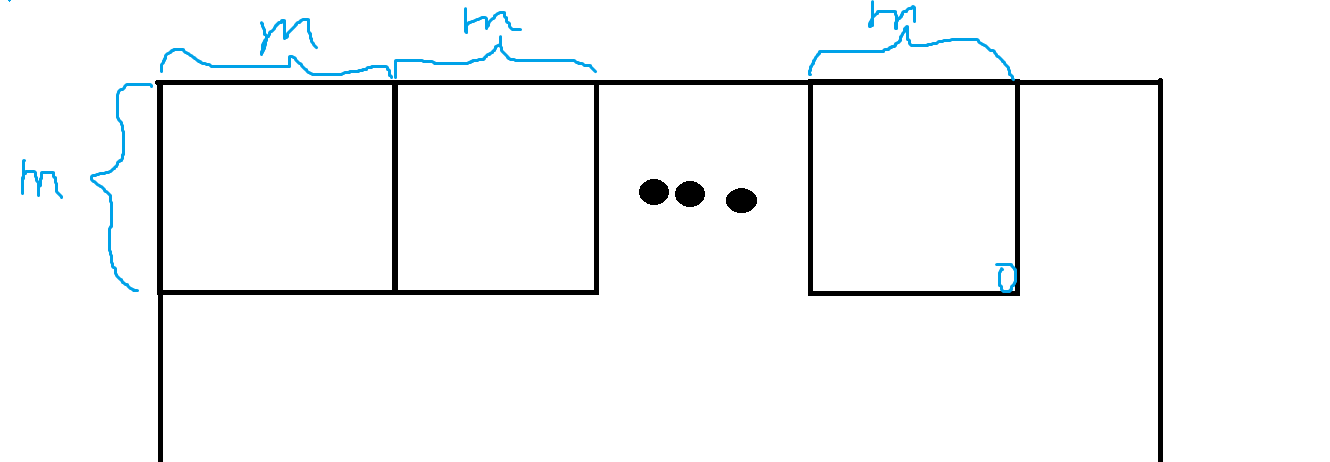
对于右边不满 (m) 的部分，我们只要在最后一个矩形的右下角填 (0)，就可以把它覆盖掉。

所以我们可以得到：对于给定的 (n,m)，(1) 最多有 (n^2 - lfloor dfrac{n}{m} floor ^2) 个。

根据初一第二学期的数学知识，我们可以得到 (n^2 - lfloor dfrac{n}{m} floor ^2 = (n + lfloor dfrac{n}{m} floor)(n - lfloor dfrac{n}{m} floor))。
又因为这个东西 (= x)，所以我们将 (x) 进行拆分并求解 (n,m)，再判断是否符合条件即可。
什么？带下取整你不会求解？那直接把下取整无视掉，解出来后再判一下不就行了。

时间复杂度 (O(tsqrt{x}))。

Code

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int T,x;
int main()
{
	scanf("%d",&T);
	while(T--)
	{
		scanf("%d",&x);
		if(x==0){puts("1 1");continue;}
		if(x==1){puts("-1");continue;}
        //特判
		for(int i=1;i*i<x;i++)
			if(x%i==0)
			{
				int a=x/i,b=i;
				int n=(a+b)/2,m=(a+b)/(a-b);//解方程可得
				if(1ll*n*n-(1ll*n/m)*(1ll*n/m)==x)//记得要判断一下
				{
					printf("%d %d
",n,m);
					goto End;
				}
			}
		puts("-1");
		End:;
	}
	return 0;
}