我们知道,由于二叉树的特性(完美情况下每次比较可以排除一半数据),对其进行查找算是比较快的了,时间复杂度为O(logN)。但是,是否存在支持时间复杂度为常数级别的查找的数据结构呢?答案是存在,那就是散列表(hash table,又叫哈希表)。散列表可以支持O(1)的插入,理想情况下可以支持O(1)的查找与删除。
散列表的基本思想很简单:
1.设计一个散列函数,其输入为数据的关键字,输出为散列值n(正整数),不同数据关键字必得出不同散列值n(即要求散列函数符合单射)
2.创建一个数组HashTable(即散列表),插入的数据存储在HashTable[n]中,n为数据的散列值且小于散列表的最大下标
这样一来,插入数据只需要计算出数据的散列值n,而后将数据存至HashTable[n]。查找数据则根据数据计算出散列值n,而后检查HashTable[n]是否存有数据即可,删除同理。这些操作都是O(1)。
但是稍加思索就会发现,上述思想是不可能在任意情况下都实现的:
一来,不可能任意情况下都有单射的散列函数,比如数据关键字为任意整数时,关键字-a与a该如何映射?
二来,即使散列函数是单射,散列表的大小也不可能总是保证大于所有可能的散列值,比如数据关键字为正整数,那么散列函数只需要令散列值等于数据关键字即可保证单射,但是如果数据总量为1000,而数据的可能最大值为10000000,难道我们创建一个大小为10000000的散列表吗?
也就是说,我们实际实现散列表时,必须面对这两个问题:
1.如何实现一个尽可能“接近”单射的散列函数
2.当不同数据关键字散列值相同时,如何处理这种冲突
第一个问题显然是因情而异的,只有给定了数据类型和一定的数据特性,才能写出对应的、好的散列函数。比如数据的key为随机正整数时,简单的散列函数是直接返回key%tableSize,这样做也没有多大问题。但是如果知道散列表的tableSize为100,且数据的key个位和十位必然为0,那么这样的散列函数就是不行的,必须修改。
也就是说,第一个问题是不存在普适性解法的,实现一个良好的散列函数本身又是另一件算法设计的事情,所以我们对于第一个问题不进行深入讨论。接下来的讨论假定这样的情形:输入的数据(关键字)为长度不超过20的字符串,且散列函数如下:
//简单的散列函数,将字符串中字符的ASCII码值相加,然后返回其与tableSize求余后的结果 unsigned int Hash(const char *target,unsigned int tableSize) { unsigned int HashVal = 0; while (*target != '�') HashVal += *target++; return HashVal%tableSize; }
那么第二个问题呢?当不同数据映射到相同散列值时的冲突,是否存在普适性的解法?答案是存在,并且解法有很多种(但是此处只给出一种的代码,其他解法只提出思路)
常见的处理散列冲突的解法有三种:分离链接,开放定址,双散列。我们将给出分离链接法的代码,其他两种则略做讨论。
分离链接法的思想很简单:如果多个数据都映射到了n,那就让这多个数据都待在HashTable[n]。
显然,要让多个数据都待在HashTable[n]处,那么HashTable的元素类型必然不是与数据相同的类型(如果是的话,HashTable[n]处只可能存下一个数据),而应该是一个链表。
举例来说,假定tableSize为7,根据已给的散列函数,关键字"ac"和"bb"的散列值均为0,则散列表在插入"ac"和"bb"后应如下:
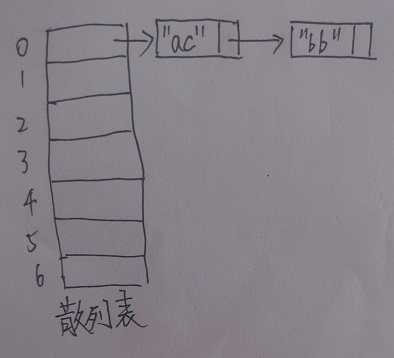
那么使用分离链接的散列表的查找方法也就是:计算出给定数据的散列值n,找到HashTable[n](一个链表),在HashTable[n]这个链表中遍历,查找是否存在给定数据。删除的实现则是在查找的基础上实施链表的删除方法即可。
不难看出,良好的散列函数是极其重要的,假设散列函数总是给出相同的散列值,那么使用分离链接法的散列表最终就成了一个链表(所有数据都映射散列值n,于是所有数据都存储在了链表HashTable[n]中)
现在,我们可以开始一步步实现一个散列表了,其散列函数我们在上面已经给出,其处理冲突的方法为分离链接。
首先,HashTable的元素是链表,所以必须给出链表结点的定义:
#define STRSIZE 20 struct ListNode { char str[STRSIZE]; struct ListNode *next; }; typedef struct ListNode *List; typedef List Position; //Position用于查找和删除
接下来是设计HashTable本身,即确定HashTable的元素类型,最简单的办法是令struct ListNode作为HashTable的类型:
struct ListNode HashTable[TABLESIZE];
但这样将带来一个问题:如何判断HashTable[n]中是空的还是只有一个元素?所以我们令List作为HashTable的元素类型,即令HashTable的元素为指向链表第一个元素的指针。这样一来,如果HashTable[n]处的链表为空,则HashTable[n]就等于NULL。
List HashTable[TABLESIZE];
但是为了使我们的散列表更有适应性,我们希望令tableSize作为一个变量,即散列表的大小可以根据编程需要来给定,于是我们将散列表设计成如下结构,并在程序中使用指针来访问散列表。同时,我们给出初始化散列表的代码:
struct HashTbl { unsigned int size; List *table; //table才是真正的那个散列表 }; typedef struct HashTbl *HashTable; //我们访问散列表将通过指针,因为例如查找这样的函数需要散列表作为参数,如果传入一个struct HashTbl,不如传入一个struct HashTbl * //根据给定大小创建散列表 HashTable Initialize(unsigned int tableSize) { //创建散列表头,并根据给定大小tableSize创建表头中的散列表 HashTable h = (HashTable)malloc(sizeof(struct HashTbl)); h->size = tableSize; h->table = (List *)malloc(sizeof(List)*tableSize); //将散列表的每个元素(指向链表第一个元素的指针)初始化为NULL for (int i = 0;i < tableSize;++i) h->table[i] = NULL; return h; }
接下来是插入操作的代码
//将字符串source插入到h中的散列表 void Insert(HashTable h, const char *source) { //此处实质为Find()操作,但为了顺便求出source的散列值,我们不直接使用Find() //若source已在散列表中,我们直接返回 unsigned int HashVal = Hash(source, h->size); Position p = h->table[HashVal]; while (p != NULL && strcmp(p->str, source)) { p = p->next; } if (p != NULL) return; //若source不在散列表中,我们计算source的散列值,并将source插入到散列表的对应位置 Position newNode = (Position)malloc(sizeof(struct ListNode)); strcpy_s(newNode->str, STRSIZE, source); newNode->next = h->table[HashVal]; h->table[HashVal] = newNode; }
查找和删除操作都不难(查找的代码在插入中已经实现了),此处不予赘述。
接下来我们谈谈什么是开放定址法。
首先,根据散列表的基本思想,如果一个数据散列值为n,那它就应该“定址”于HashTable[n]处,这也可以说是分离链接法的根本(既然你们散列值为n,那你们就都得待在HashTable[n])
而开放定址法就顾名思义了,数据不再是“定址”的,一个数据关键字散列值为n,但其不一定位于HashTable[n]处。
开放定址法是这么做的:如果数据关键字散列值为n,则先尝试将其插入到HashTable[n]处,若HashTable[n]处已有数据,则插入到HashTable[(n+1)%tableSize]处,如果该处亦有数据,则插入到HashTable[(n+2)%tableSize]处,以此类推,直至遇到某处为空,插入数据至该处,或者走遍散列表依然没有空处,则插入失败。这样的插入称为“线性探测”
查找操作则是:计算散列值n,比较HashTable[n]与数据,若相同则找到,否则比较HashTable[(n+1)%tableSize]与数据,以此类推,直至到了某个空结点,则说明没找到
删除操作则必须是懒惰删除,因为若实质删除,则开放定址法的插入和查找都将乱套,也就是说HashTable的元素类型必然是一个包含数据类型的新结构体,其存在frequency域用于表示数据是否存在或相同数据存在多少个。
开放定址法相比于分离链接法可以节省指针空间,但也带来了两个问题:
1.如果插入数据时,总是按照n=n+1的形式去找一个空的HashTable[n],那么数据很容易出现“集中”现象。(比如插入三个散列值为80的数据,再插入两个散列值为81和83的数据,那么它们都将“挤在”HashTable[80]到HashTable[84]间)
2.设装填因子Ω=已插入数据个数/tableSize,那么Ω越接近于1,开放定址法的各项操作就越慢,而且很可能出现插入失败
对于第一个问题,有两种改善的办法,一种是采用“平方探测”形式的插入,即令n+=2*++n-1,而不是n=n+1,这样可以减少一次集中,但相同散列值的数据依然可能出现“二次集中”现象。另一种办法则是双散列,即出现冲突时令n=n*hash2(key),本质上来说,平方探测、线性探测和双散列是相似的,都是在出现冲突时另寻一处存放数据,当然,这个另寻一处必须是可重现的。
对于第二个问题,解决办法是再散列,即当Ω大于一定程度后,重新创建新的、更大的散列表,而后将数据移至新散列表。也就是“再次散列”。
使用分离链接法的散列表的示例程序代码:
https://github.com/nchuXieWei/ForBlog-----HashTable