最小树形图就是在有向图上,以某一点作为根的一棵最小生成树。
这个算法是基于贪心和缩点的思想。
步骤:
(1)先求出最短弧集合E0(图上所有点的边权最小的入边的集合);
(2)如果E0不存在,则图的最小树形图也不存在,跳出循环;
(3)如果E0存在且不具有环,则E0就是最小树形图,跳出循环;
(4)如果E0存在但是存在有向环,则把这个环收缩成一个点u,形成新的图G1,然后对G1继续求其的最小树形图,返回(1)。
具体实现
int ans = 0; //记录加入最小树形图中的边的边权
初始化
int root; //根节点
int cnt; //环的个数 int ine[maxn]; //某一点的所有入边中的边权的最小值 int pre[maxn]; //某一点的所有入边中的边权最小的边所连接的另一点 int id[maxn]; //当前点所属的环 int vis[maxn]; //在找环的过程中,当前点是由哪一点延展过来的
注意,以上六个变量在每次缩点完成求出新图后都需要重置。
首先枚举每条边,看是否能更新这条边终点的最短弧。
for(int i = 1; i <= n; i++) ine[i] = INF;
//初始化 for(int i = 1; i <= m; i++) { int u = e[i].uu; int v = e[i].vv; if(u != v && e[i].val < ine[v]) { ine[v] = e[i].val; pre[v] = u; } }
枚举完成后,检查否每个点都遍历到了。如果没有,说明不存在最小树形图。
for(int i = 1; i <= n; i++) if(i != root && ine[i]==INF) return -1;
找出最短弧集合中的环。
cnt = 0; for(int i = 1; i <= n; i++) { id[i] = 0; vis[i] = 0; } //初始化 for(int i = 1; i <= n; i++) { if(i == root)continue; ans += ine[i]; int v = i; while(vis[v]!=i && !id[v] && v!=root) { vis[v] = i; v = pre[v]; } if(!id[v] && v != root) { id[v] = ++cnt; for(int u = pre[v]; u!=v; u = pre[u]) id[u] = cnt; } } if(!cnt)break; for(int i = 1; i <= n; i++) if(!id[i]) id[i] = ++cnt;
根节点无入度,不可能成环,跳过;
设当前点为v。
将统计最小树形图边权的ans加入当前点的最小弧的边权ine[v]。
从点v出发,向前寻找它的祖先(即它是由哪个点发出的边作为最小弧),如果最后又找回这一点v,说明有环存在。
- vis[v] == i 说明这一点是本次由i点延伸过来的,即成环;
- 这里的i不能写成true,假设有一条“v→v'→...→root”的链,上次从点v'开始枚举,vis[v']就被标记了,而这次从v找到了v',不能说明成环。
- id[v] 表示这一点已经被染过色,已经在另一个环里;
- 如果为根节点root,因为它没有入度,所以就会找到编号为0的点……引起各种错误。
如果排除了后两种情况,则一定是成环。
再次遍历这个环,将环中的每个点染上相同的颜色(cnt),即标出是第几个环。
全部完成后,检查环的个数。若无环,则返回答案。
没有被加入环中的点,自己单独作为一个环,方便下一步调用。
缩环为点,修改边权
for(int i = 1; i <= m; i++) { int u = e[i].uu; int v = e[i].vv; e[i].uu = id[u]; e[i].vv = id[v]; if(id[u] != id[v]) e[i].val -= ine[v]; } root = id[root]; n = cnt;
枚举每条边,将该点的起点和终点均改为起点和终点所在环的序号,
即把边由连接点-点变成了环-环。
若这条边(u,v)连接两个不在同一环上的点,则边权减去ine[v]。
这部分一开始不太好理解。

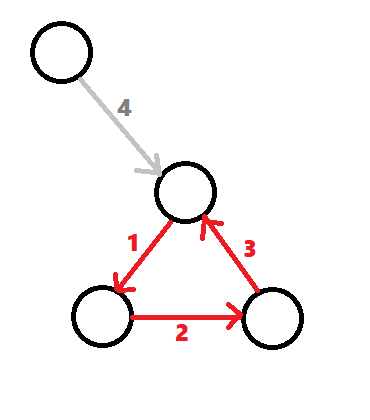
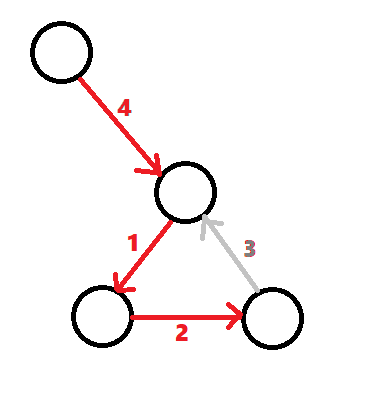
对于第一张图求最短弧,得到了第二张图。但是求出的集合中有弧,必须删掉环中的一条边。
把环看作一个点,需要更新连到这个环上的边的边权。因为此时已经把环中的所有边都加入了答案中,所以如果向树形图中加入边(u,v),必须删掉环中连接v的边,边权即为ine[v]。直接将当前枚举的边的边权减去ine[v],则说明若加入这条边(u,v),一定删去环上与v相连的边。
最后统计缩点后点的个数和根节点的编号,进入下一次循环。
完整代码如下
#include<cstdio> #include<iostream> #include<cmath> #include<cstring> #define MogeKo qwq using namespace std; const int maxn = 1e5+10; const int INF = 0x3f3f3f3f; int n,m,root; int ine[maxn],pre[maxn],id[maxn],vis[maxn]; struct edge { int uu,vv,val; } e[maxn]; int zhuliu() { int ans = 0; while(1) { for(int i = 1; i <= n; i++) ine[i] = INF; for(int i = 1; i <= m; i++) { int u = e[i].uu; int v = e[i].vv; if(u != v && e[i].val < ine[v]) { ine[v] = e[i].val; pre[v] = u; } } for(int i = 1; i <= n; i++) if(i != root && ine[i]==INF) return -1; int cnt = 0; for(int i = 1; i <= n; i++) { id[i] = 0; vis[i] = 0; } for(int i = 1; i <= n; i++) { if(i == root)continue; ans += ine[i]; int v = i; while(vis[v]!=i && !id[v] && v!=root) { vis[v] = i; v = pre[v]; } if(!id[v] && v != root) { id[v] = ++cnt; for(int u = pre[v]; u!=v; u = pre[u]) id[u] = cnt; } } if(!cnt)break; for(int i = 1; i <= n; i++) if(!id[i]) id[i] = ++cnt; for(int i = 1; i <= m; i++) { int u = e[i].uu; int v = e[i].vv; e[i].uu = id[u]; e[i].vv = id[v]; if(id[u] != id[v]) e[i].val -= ine[v]; } root = id[root]; n = cnt; } return ans; } int main() { scanf("%d%d%d",&n,&m,&root); for(int i = 1; i <= m; i++) scanf("%d%d%d",&e[i].uu,&e[i].vv,&e[i].val); printf("%d",zhuliu()); return 0; }