一、介绍
1.概念
算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。
2.扩展
递归(实例：汉诺塔问题)的两个特点：
1）调用自身
2）结束条件
二、查找
1.列表查找
从列表中查找指定元素
输入：列表、待查找元素
代码：
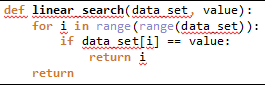
时间复杂度O(n)
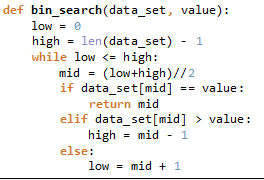
时间复杂度O(logn)
2.顺序查找
从列表第一个元素开始，顺序进行搜索，直到找到为止。
3.二分查找
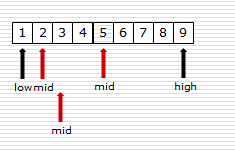
从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半,具体如下图：
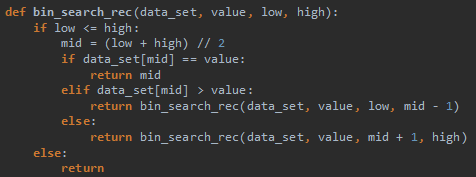
递归版本的二分查找
三、排序
以下代码都要用到timewrap.py文件，需导入才可使用。
import time def cal_time(func): def wrapper(*args, **kwargs): t1 = time.time() result = func(*args, **kwargs) t2 = time.time() print("%s running time: %s secs." % (func.__name__, t2-t1)) return result return wrapper
排序LOWB三人组：冒泡排序、插入排序、选择排序
时间复杂度：O(n2)
空间复杂度：O(1)
1.冒泡排序
原理：
-
比较相邻的元素。如果第一个比第二个大，就交换他们两个。
-
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
-
针对所有的元素重复以上的步骤，除了最后一个。
-
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。
示例代码
# 冒泡排序 import random from timewrap import * @cal_time def bubble_sort(li): for i in range(len(li) - 1): # i 表示趟数 # 第 i 趟时： 无序区：(0，len(li) - i) for j in range(0, len(li) - i - 1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] @cal_time def bubble_sort_2(li): for i in range(len(li) - 1): # i 表示趟数 # 第 i 趟时： 无序区：(0，len(li) - i) change = False for j in range(0, len(li) - i - 1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] change = True if not change: return li = list(range(10000)) # random.shuffle(li) # print(li) bubble_sort_2(li) print(li)
注：如果冒泡排序中执行一趟而没有交换，则列表已经是有序状态，可以直接结束算法。
2.插入排序
原理：
⒈从有序数列和无序数列{a2,a3，…，an}开始进行排序；
⒉处理第i个元素时（i=2,3，…，n），数列{a1,a2，…，ai-1}是已有序的，而数列{ai,ai+1，…，an}是无序的。用ai与ai-1，a i-2，…，a1进行 比较，找出合适的位置将ai插入；
⒊重复第二步，共进行n-i次插入处理，数列全部有序。
示例代码：
import random from timewrap import * @cal_time def insert_sort(li): for i in range(1, len(li)): # i 表示无序区第一个数 tmp = li[i] # 摸到的牌 j = i - 1 # j 指向有序区最后位置 while li[j] > tmp and j >= 0: #循环终止条件： 1. li[j] <= tmp; 2. j == -1 li[j+1] = li[j] j -= 1 li[j+1] = tmp li = list(range(10000)) random.shuffle(li) print(li) insert_sort(li) print(li)
3.选择排序
原理：
选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法（比如序列[5， 5， 3]第一次就将第一个[5]与[3]交换，导致第一个5挪动到第二个5后面）。
示例代码：
import random from timewrap import * @cal_time def select_sort(li): for i in range(len(li) - 1): # i 表示趟数，也表示无序区开始的位置 min_loc = i # 最小数的位置 for j in range(i + 1, len(li) - 1): if li[j] < li[min_loc]: min_loc = j li[i], li[min_loc] = li[min_loc], li[i] li = list(range(10000)) random.shuffle(li) print(li) select_sort(li) print(li)
NB三人组：快速排序、堆排序、归并排序
4.快速排序
快速排序：快
原理：
1.取一个元素p（第一个元素），使元素p归位；
2.列表被p分成两部分，左边都比p小，右边都比p大；
3.递归完成排序。
问题：最坏情况、递归
示例代码：
import random from timewrap import * import copy import sys sys.setrecursionlimit(100000) def partition(li, left, right): # ri = random.randint(left, right) # li[left], li[ri] = li[ri], li[left] tmp = li[left] while left < right: while left < right and li[right] >= tmp: right -= 1 li[left] = li[right] while left < right and li[left] <= tmp: left += 1 li[right] = li[left] li[left] = tmp return left def _quick_sort(li, left, right): if left < right: # 至少有两个元素 mid = partition(li, left, right) _quick_sort(li, left, mid-1) _quick_sort(li, mid+1, right) @cal_time def quick_sort(li): return _quick_sort(li, 0, len(li)-1) @cal_time def sys_sort(li): li.sort() li = list(range(10000)) random.shuffle(li) #sys_sort(li1) quick_sort(li)
5.归并排序
假设现在的列表分两段有序，如何将其合并成一个有序列表
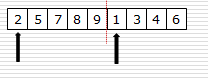
这种操作称为一次归并。
分解：将列表越分越小，直至分成一个元素。
终止条件：一个元素是有序的。
合并：将两个有序列表归并，列表越来越大。
示例代码：
import random from timewrap import * import copy import sys def merge(li, low, mid, high): i = low j = mid + 1 ltmp = [] while i <= mid and j <= high: if li[i] < li[j]: ltmp.append(li[i]) i += 1 else: ltmp.append(li[j]) j += 1 while i <= mid: ltmp.append(li[i]) i += 1 while j <= high: ltmp.append(li[j]) j += 1 li[low:high+1] = ltmp def _merge_sort(li, low, high): if low < high: # 至少两个元素 mid = (low + high) // 2 _merge_sort(li, low, mid) _merge_sort(li, mid+1, high) merge(li, low, mid, high) print(li[low:high+1]) def merge_sort(li): return _merge_sort(li, 0, len(li)-1) li = list(range(16)) random.shuffle(li) print(li) merge_sort(li) print(li)
6.堆排序
前转小知识 二叉树是度不超过2的树 满二叉树与完全二叉树
（完全）二叉树可以用列表来存储，通过规律可以从父亲找到孩子或从孩子找到父亲。
堆排序的过程
1.建立堆
2.得到堆顶元素，为最大元素
3.去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。
4.堆顶元素为第二大元素。
5.重复步骤3，直到堆变空。
示例代码：
from timewrap import * import random def _sift(li, low, high): """ :param li: :param low: 堆根节点的位置 :param high: 堆最有一个节点的位置 :return: """ i = low # 父亲的位置 j = 2 * i + 1 # 孩子的位置 tmp = li[low] # 原省长 while j <= high: if j + 1 <= high and li[j + 1] > li[j]: # 如果右孩子存在并且右孩子更大 j += 1 if tmp < li[j]: # 如果原省长比孩子小 li[i] = li[j] # 把孩子向上移动一层 i = j j = 2 * i + 1 else: li[i] = tmp # 省长放到对应的位置上(干部) break else: li[i] = tmp # 省长放到对应的位置上(村民/叶子节点) def sift(li, low, high): """ :param li: :param low: 堆根节点的位置 :param high: 堆最有一个节点的位置 :return: """ i = low # 父亲的位置 j = 2 * i + 1 # 孩子的位置 tmp = li[low] # 原省长 while j <= high: if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子存在并且右孩子更大 j += 1 if tmp < li[j]: # 如果原省长比孩子小 li[i] = li[j] # 把孩子向上移动一层 i = j j = 2 * i + 1 else: break li[i] = tmp @cal_time def heap_sort(li): n = len(li) # 1. 建堆 for i in range(n//2-1, -1, -1): sift(li, i, n-1) # 2. 挨个出数 for j in range(n-1, -1, -1): # j表示堆最后一个元素的位置 li[0], li[j] = li[j], li[0] # 堆的大小少了一个元素 （j-1） sift(li, 0, j-1) li = list(range(10000)) random.shuffle(li) heap_sort(li) print(li) # li=[2,9,7,8,5,0,1,6,4,3] # sift(li, 0, len(li)-1) # print(li)
堆排序--内置模块
优先队列：一些元素的集合，POP操作每次执行都会从优先队列中弹出最大（或最小）的元素。
堆——优先队列
Python内置模块——heapq
heapify(x)
heappush(heap, item)
heappop(heap)
利用heapq模块实现堆排序
示例代码：
import heapq, random li = [5,8,7,6,1,4,9,3,2] heapq.heapify(li) print(heapq.heappop(li)) print(heapq.heappop(li)) def heap_sort(li): heapq.heapify(li) n = len(li) new_li = [] for i in range(n): new_li.append(heapq.heappop(li)) return new_li li = list(range(10000)) random.shuffle(li) # li = heap_sort(li) # print(li) print(heapq.nlargest(100, li))
四、树与二叉树
树是一种数据结构 比如：目录结构 树是一种可以递归定义的数据结构 树是由n个节点组成的集合： 如果n=0，那这是一棵空树； 如果n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。 一些概念 根节点、叶子节点 树的深度（高度） 树的度 孩子节点/父节点 子树
可以形象的用下图来表示：
1.特殊且常用的树
二叉树：度不超过2的树（节点最多有两个叉）
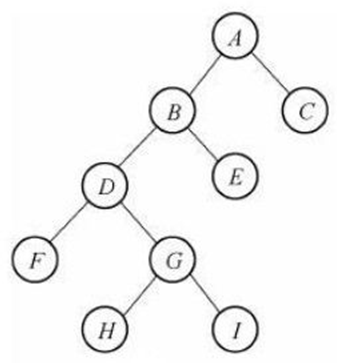
2.两种特殊的二叉树
满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
3.二叉树的存储方式
链式存储方式 顺序存储方式（列表）