题目原文
703. 数据流中的第 K 大元素
设计一个找到数据流中第 k 大元素的类(class)。注意是排序后的第 k 大元素,不是第 k 个不同的元素。
请实现 KthLargest 类:
KthLargest(int k, int[] nums)使用整数k和整数流nums初始化对象。int add(int val)将val插入数据流nums后,返回当前数据流中第k大的元素。
示例:
输入: ["KthLargest", "add", "add", "add", "add", "add"] [[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]] 输出: [null, 4, 5, 5, 8, 8] 解释: KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]); kthLargest.add(3); // return 4 kthLargest.add(5); // return 5 kthLargest.add(10); // return 5 kthLargest.add(9); // return 8 kthLargest.add(4); // return 8提示:
1 <= k <= 1040 <= nums.length <= 104-104 <= nums[i] <= 104-104 <= val <= 104- 最多调用
add方法104次 - 题目数据保证,在查找第
k大元素时,数组中至少有k个元素
尝试解答
寒假月期间的力扣主题是滑动窗口,大部分题目比较弟弟,但也有个别题目或新颖清奇或夯实基础,例如这道题虽然是简单难度,但是其主要考察的内容是经典的topK,topK的标准解法一般是写一个堆数据结构,博主还是太菜了没有想到这种解法,解答费了不少时间,最后检验一共十个测试用例,卡在了测试时间复杂度的第七个超长用例没有AC,上垃圾代码:
1 class KthLargest { 2 public int k; 3 public int[] nums; 4 public KthLargest(int k, int[] nums) { 5 this.k = k; 6 Arrays.sort(nums); 7 this.nums = nums; 8 // for(int i=0;i<nums.length;i++){ 9 // System.out.print(this.nums[i]); 10 // } 11 } 12 13 public int add(int val) { 14 int[] new_nums = new int[nums.length+1]; 15 boolean vias = false; 16 int new_index = 0; 17 int index = 0; 18 while(new_index<new_nums.length && index<nums.length){ 19 if(val>nums[index]){ 20 new_nums[new_index] = nums[index]; 21 } 22 else{ 23 if(!vias){ 24 new_nums[new_index] = val; 25 index--; 26 vias = true; 27 } 28 else{ 29 new_nums[new_index] = nums[index]; 30 } 31 } 32 new_index++; 33 index++; 34 } 35 if(!vias){ 36 new_nums[new_nums.length-1] = val; 37 } 38 for(int i=0;i<new_nums.length;i++){ 39 System.out.print(new_nums[i]); 40 System.out.print(' '); 41 } 42 System.out.println(); 43 this.nums = new_nums; 44 return new_nums[new_nums.length-k]; 45 } 46 } 47 48 /** 49 * Your KthLargest object will be instantiated and called as such: 50 * KthLargest obj = new KthLargest(k, nums); 51 * int param_1 = obj.add(val); 52 */
标准题解
方法一:使用heapq库
1 class KthLargest: 2 3 def __init__(self, k: int, nums: List[int]): 4 self.heap = [] 5 self.k = k 6 for num in nums: 7 heapq.heappush(self.heap,num) 8 if len(self.heap) > k: 9 heapq.heappop(self.heap) 10 11 12 def add(self, val: int) -> int: 13 heapq.heappush(self.heap,val) 14 if len(self.heap) > self.k: 15 heapq.heappop(self.heap) 16 return self.heap[0] 17 18 19 ##作者:MiloMusiala 20 ##链接:https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/solution/python-dong-hua-shou-xie-shi-xian-dui-by-ypz2/ 21 ##来源:力扣(LeetCode) 22 ##著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
方法二:手写实现
我们通过自己手写来详细刨析一下堆这个数据结构到底是怎么实现的。
堆的特点:
内部数据是有序的
可以弹出堆顶的元素,大顶堆就是弹出最大值,小顶堆就是弹出最小值
每次加入新元素或者弹出堆顶元素后,调整堆使之重新有序仅需要O(logn)的时间
支持在线算法
堆的本质:
它是一个完全二叉树
实现的时候我们不需要建造一个树,改用一个数组即可
那么我们是如何把一个完全二叉树和一个数组关联到一起的呢?
给树的节点编号,节点的编号就是元素在数组中的下标
幻灯片1.JPG
于是我们发现一个很重要的结论:
已知一个节点的编号为index,那么它的父节点的编号为:
father_index=⌊index−12⌋father\_index = lfloor {index-1 over 2}
floor father_index=⌊2index−1⌋
左孩子节点的编号为
left_index=index∗2+1left\_index = index * 2 + 1 left_index=index∗2+1
右孩子节点的编号为
right_index=index∗2+2right\_index = index * 2 + 2 right_index=index∗2+2
如何调整堆
1.添加元素
把新数据添加到树的最后一个元素,也就是数组的末尾
把末尾节点向上调整


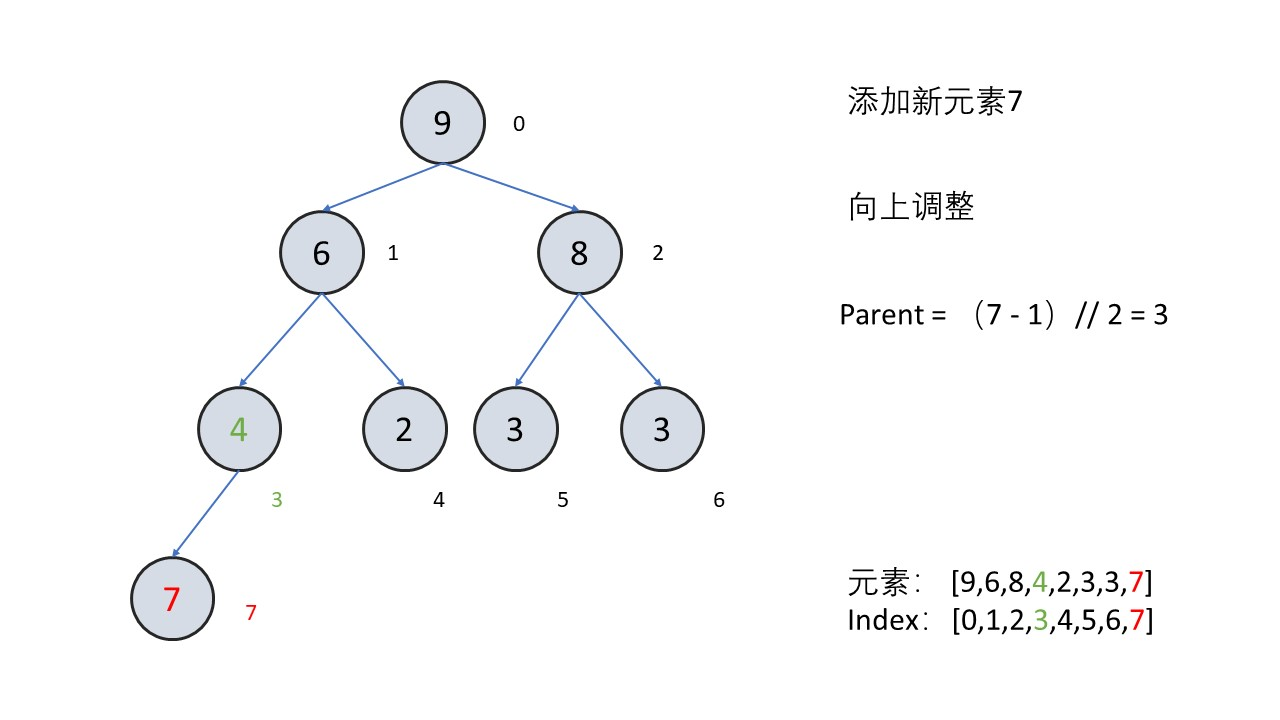



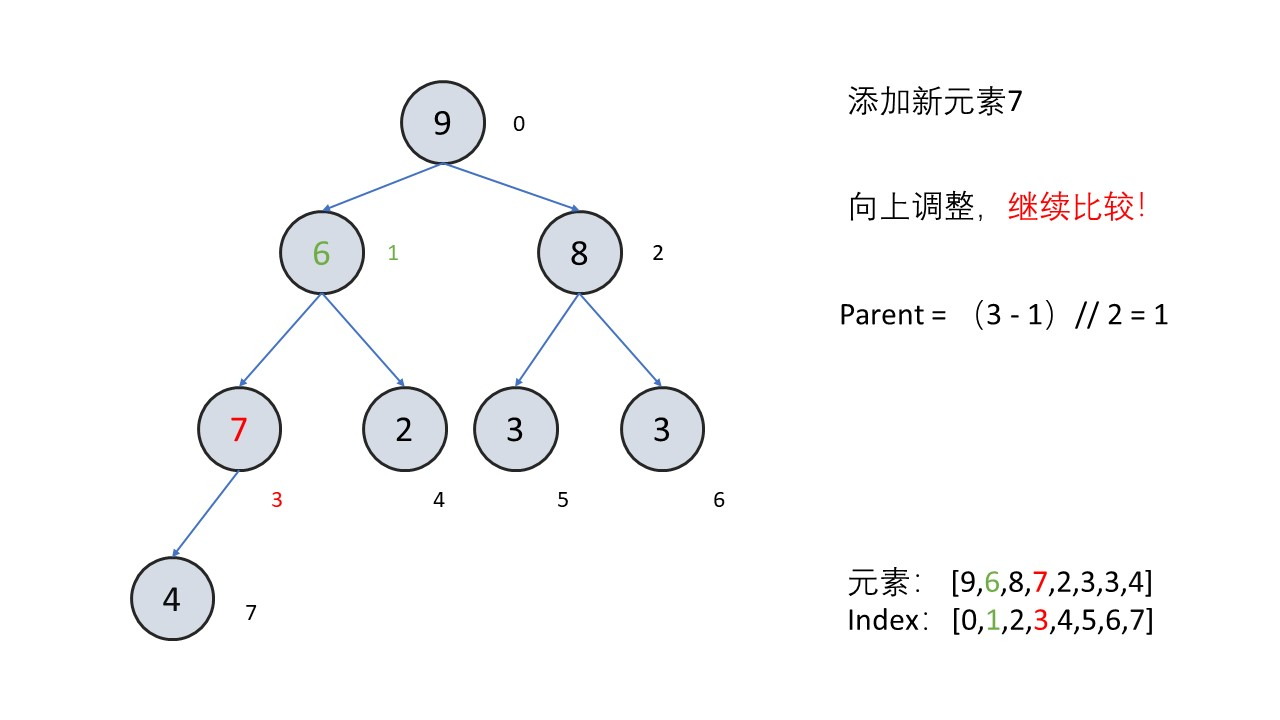
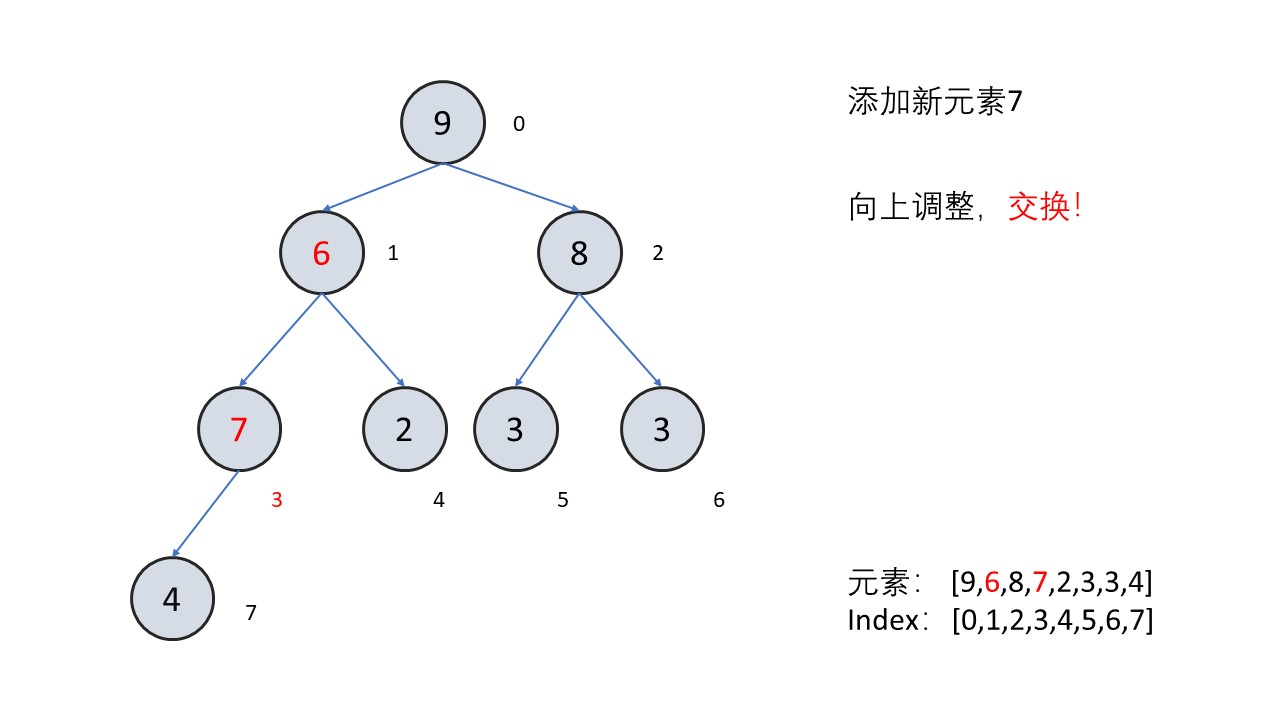

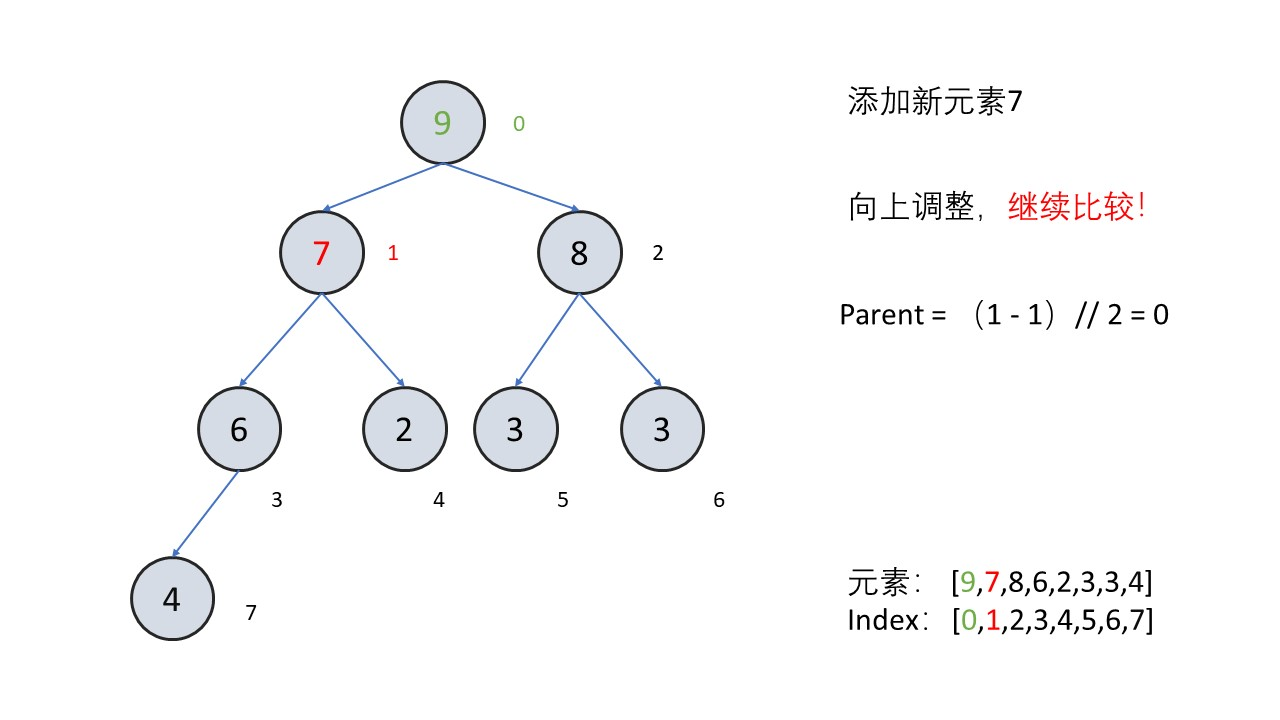

- 弹出堆顶
- 交换根节点与最后一个节点的值
- 删除最后一个节点
- 把根节点向下调整
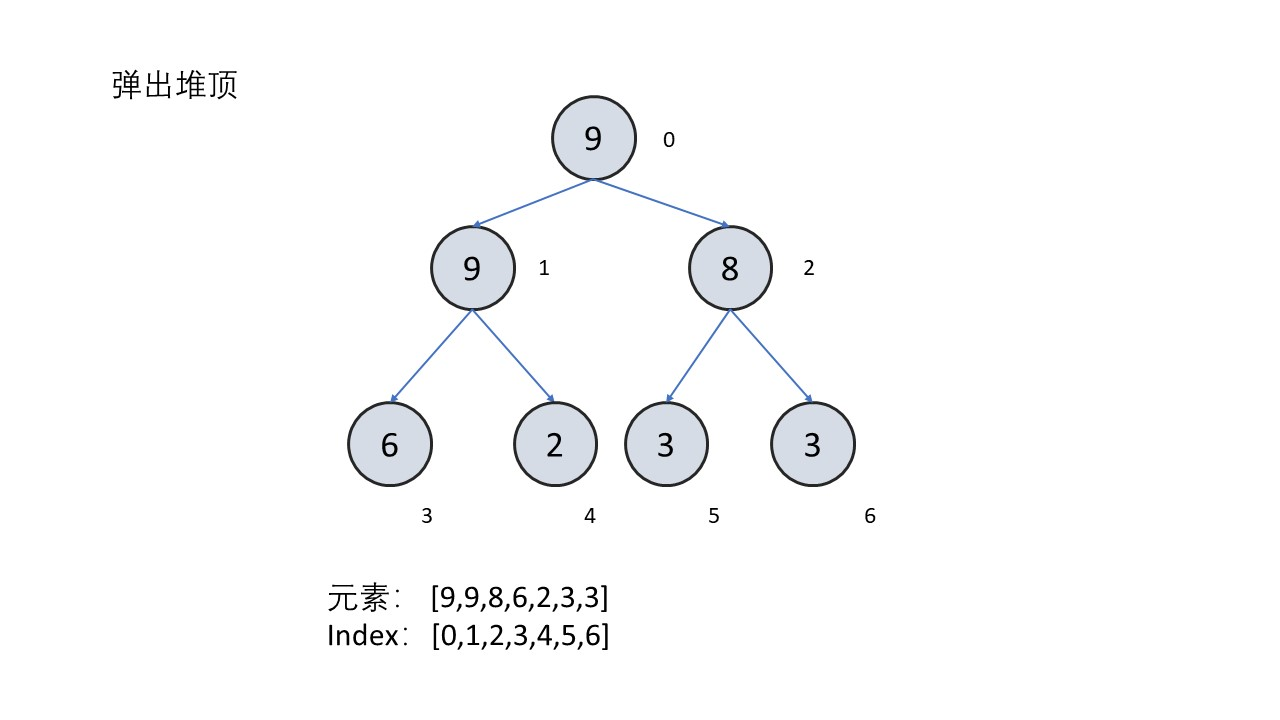


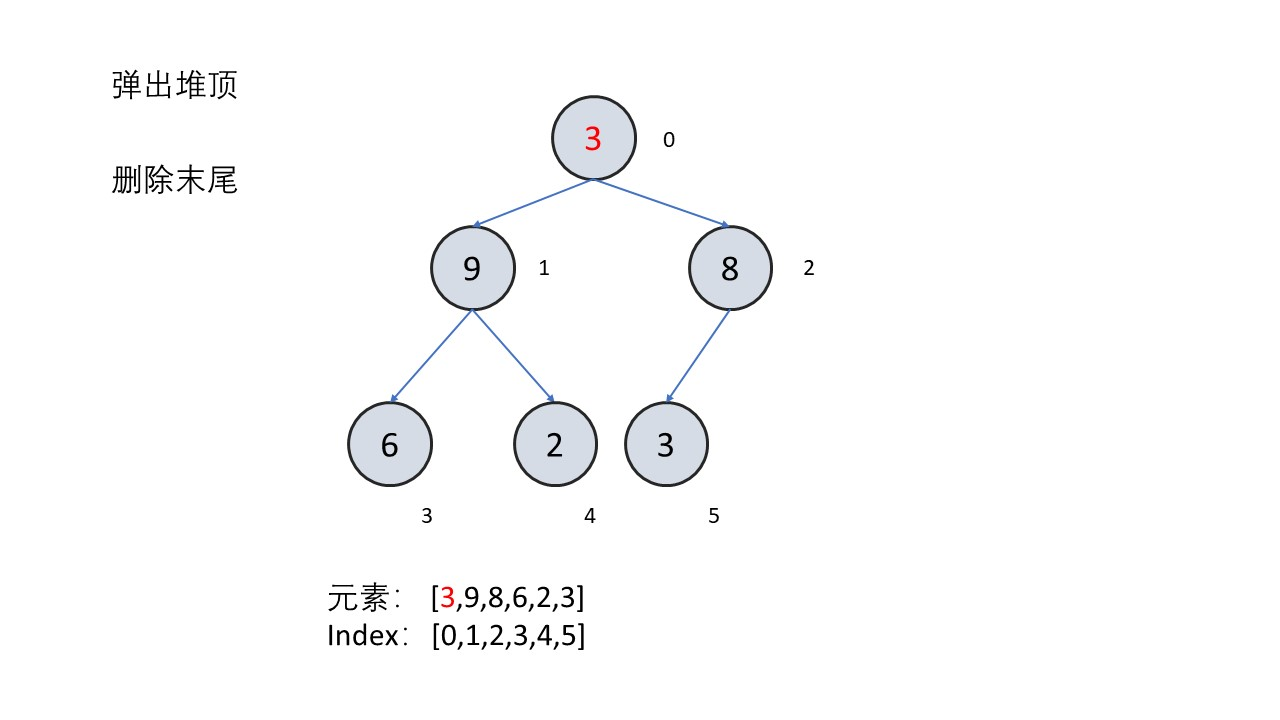


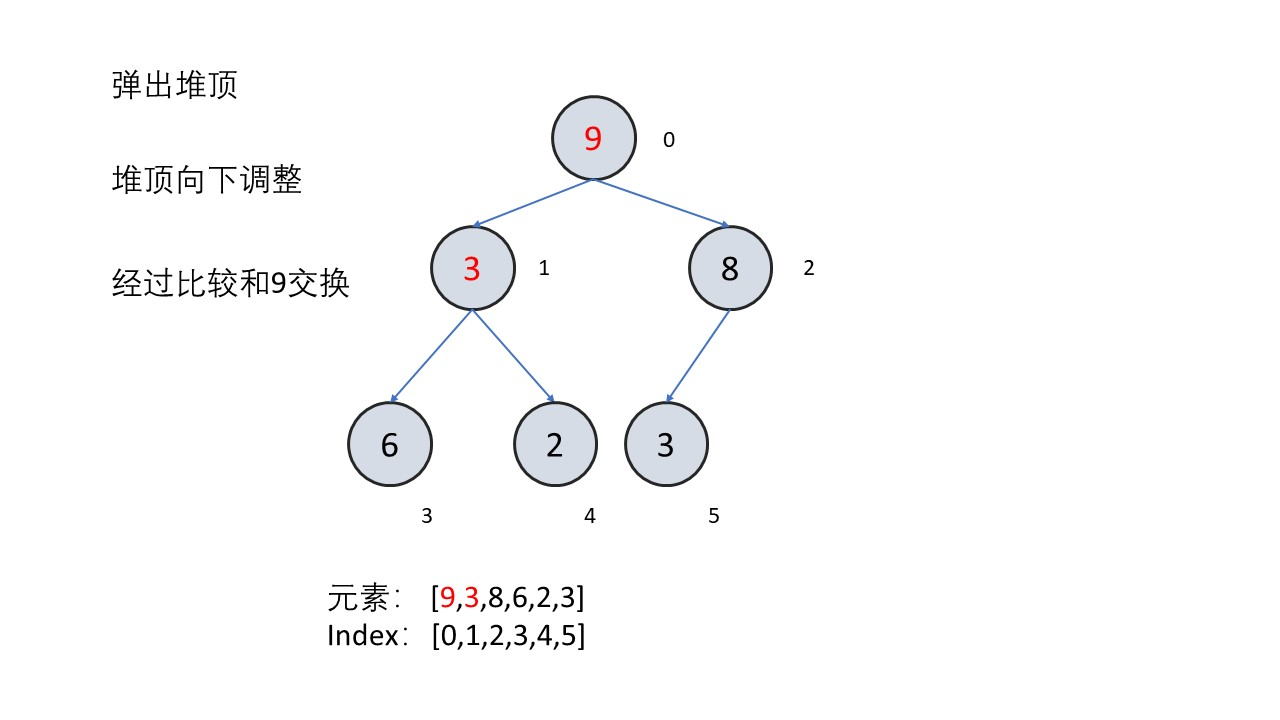




所以需要写的函数有
1、初始化
1 def __init__(self,desc=False): 2 """ 3 初始化,默认创建一个小顶堆 4 """ 5 self.heap = [] 6 self.desc = desc
2、堆的大小
@property def size(self): return len(self.heap)
3、返回堆顶元素
1 def top(self): 2 if self.size: 3 return self.heap[0] 4 return None
4、添加元素
1 def push(self,item): 2 """ 3 添加元素 4 第一步,把元素加入到数组末尾 5 第二步,把末尾元素向上调整 6 """ 7 self.heap.append(item) 8 self._sift_up(self.size-1)
5、弹出堆顶元素
1 def pop(self): 2 """ 3 弹出堆顶 4 第一步,记录堆顶元素的值 5 第二步,交换堆顶元素与末尾元素 6 第三步,删除数组末尾元素 7 第四步,新的堆顶元素向下调整 8 第五步,返回答案 9 """ 10 item = self.heap[0] 11 self._swap(0,self.size-1) 12 self.heap.pop() 13 self._sift_down(0) 14 return item
6、判断两个元素的大小关系,这里有个小trick
1 def _smaller(self,lhs,rhs): 2 return lhs > rhs if self.desc else lhs < rhs 3 4 5 作者:MiloMusiala 6 链接:https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/solution/python-dong-hua-shou-xie-shi-xian-dui-by-ypz2/ 7 来源:力扣(LeetCode) 8 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
7、向上调整
1 def _sift_up(self,index): 2 """ 3 向上调整 4 如果父节点和当前节点满足交换的关系 5 (对于小顶堆是父节点元素更大,对于大顶堆是父节点更小), 6 则持续将当前节点向上调整 7 """ 8 while index: 9 parent = (index-1) // 2 10 11 if self._smaller(self.heap[parent],self.heap[index]): 12 break 13 14 self._swap(parent,index) 15 index = parent
8、向下调整
1 def _sift_down(self,index): 2 """ 3 向下调整 4 如果子节点和当前节点满足交换的关系 5 (对于小顶堆是子节点元素更小,对于大顶堆是子节点更大), 6 则持续将当前节点向下调整 7 """ 8 # 若存在子节点 9 while index*2+1 < self.size: 10 smallest = index 11 left = index*2+1 12 right = index*2+2 13 14 if self._smaller(self.heap[left],self.heap[smallest]): 15 smallest = left 16 17 if right < self.size and self._smaller(self.heap[right],self.heap[smallest]): 18 smallest = right 19 20 if smallest == index: 21 break 22 23 self._swap(index,smallest) 24 index = smallest
9、交换两个元素
1 def _swap(self,i,j): 2 self.heap[i],self.heap[j] = self.heap[j],self.heap[i] 3 4 5 作者:MiloMusiala 6 链接:https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/solution/python-dong-hua-shou-xie-shi-xian-dui-by-ypz2/ 7 来源:力扣(LeetCode) 8 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
完整代码:
1 class Heap: 2 def __init__(self,desc=False): 3 """ 4 初始化,默认创建一个小顶堆 5 """ 6 self.heap = [] 7 self.desc = desc 8 9 @property 10 def size(self): 11 return len(self.heap) 12 13 def top(self): 14 if self.size: 15 return self.heap[0] 16 return None 17 18 def push(self,item): 19 """ 20 添加元素 21 第一步,把元素加入到数组末尾 22 第二步,把末尾元素向上调整 23 """ 24 self.heap.append(item) 25 self._sift_up(self.size-1) 26 27 def pop(self): 28 """ 29 弹出堆顶 30 第一步,记录堆顶元素的值 31 第二步,交换堆顶元素与末尾元素 32 第三步,删除数组末尾元素 33 第四步,新的堆顶元素向下调整 34 第五步,返回答案 35 """ 36 item = self.heap[0] 37 self._swap(0,self.size-1) 38 self.heap.pop() 39 self._sift_down(0) 40 return item 41 42 def _smaller(self,lhs,rhs): 43 return lhs > rhs if self.desc else lhs < rhs 44 45 def _sift_up(self,index): 46 """ 47 向上调整 48 如果父节点和当前节点满足交换的关系 49 (对于小顶堆是父节点元素更大,对于大顶堆是父节点更小), 50 则持续将当前节点向上调整 51 """ 52 while index: 53 parent = (index-1) // 2 54 55 if self._smaller(self.heap[parent],self.heap[index]): 56 break 57 58 self._swap(parent,index) 59 index = parent 60 61 def _sift_down(self,index): 62 """ 63 向下调整 64 如果子节点和当前节点满足交换的关系 65 (对于小顶堆是子节点元素更小,对于大顶堆是子节点更大), 66 则持续将当前节点向下调整 67 """ 68 # 若存在子节点 69 while index*2+1 < self.size: 70 smallest = index 71 left = index*2+1 72 right = index*2+2 73 74 if self._smaller(self.heap[left],self.heap[smallest]): 75 smallest = left 76 77 if right < self.size and self._smaller(self.heap[right],self.heap[smallest]): 78 smallest = right 79 80 if smallest == index: 81 break 82 83 self._swap(index,smallest) 84 index = smallest 85 86 def _swap(self,i,j): 87 self.heap[i],self.heap[j] = self.heap[j],self.heap[i] 88 89 class KthLargest: 90 91 def __init__(self, k: int, nums: List[int]): 92 self.heap = Heap() 93 self.k = k 94 for num in nums: 95 self.heap.push(num) 96 if self.heap.size > k: 97 self.heap.pop() 98 99 100 def add(self, val: int) -> int: 101 self.heap.push(val) 102 if self.heap.size > self.k: 103 self.heap.pop() 104 return self.heap.top() 105 106 107 108 ##作者:MiloMusiala 109 ##链接:https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/solution/python-dong-hua-shou-xie-shi-xian-dui-by-ypz2/ 110 ##来源:力扣(LeetCode) 111 ##著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
思路差距
topK问题在各大互联网面试题目中比较常见,一般是往一串有序数据中频繁执行插入、删除的操作,为优化此类操作,一般都会使用堆这类数据结构,各语言对于堆都有现成的类,比如java语言的PriorityQueue,python语言的heapq,菜鸡博主认为若是为了提高代码水平,应该做到理解堆的原理并能手撕堆数据结构。
技术差距
手撕堆数据结构、堆排序还需练习