摘要
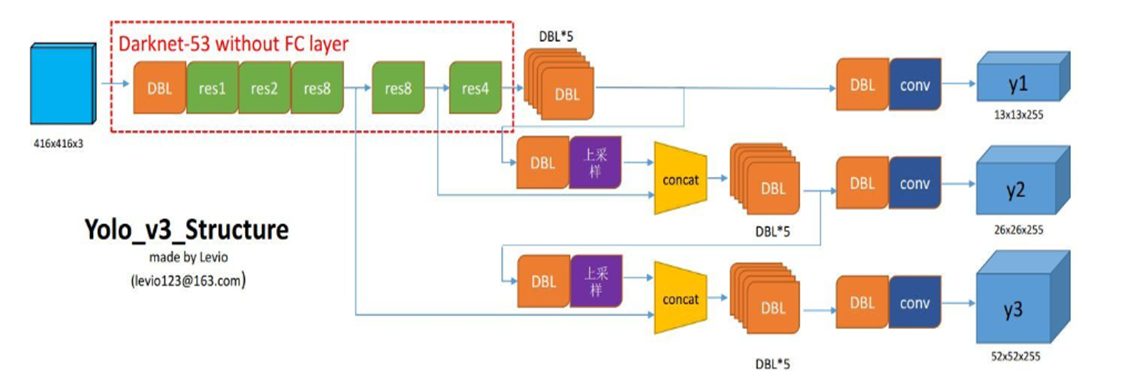
在损失函数计算的过程中,需要对模型的输出即 feats进行相关信息的计算。 ---- 在yolo_head中
当前小网格相对于大网格的位置(也可以理解为是相对于特征图的位置)
loss的计算时每一层结果均与真值进行误差的累加计算。
YOLO v3的损失函数与v1 的损失函数略有不同。损失函数的计算是在对应特征图上的,而不是将其转化至416,416的图上,或者转化到原图上。
YOLO v3使用多目标的方式进行分类,而不是使用softmax。

一张图像的输出其最终对应的输出尺寸为1×(3×(13×13+26×26+52×52)) × (5+k) = 1×10647 × (5+k)
那其实根据真值篇所述,"正样本只要IOU最大的,而不是超过某一阈值的都是正样本",置信度正负样本比例高达1:10647, 也就是说,在10647中,正样本只有一个。所以计算损失时使用的是SSE计算,而不是平均,因为平均损失会接近于0。
代码解读
损失层
在模型的训练过程中,不断调整网络中的参数,优化损失函数loss的值达到最小,完成模型的训练。在YOLO v3中,损失函数yolo_loss封装在自定义Lambda的损失层中,作为模型的最后一层,参于训练。损失层Lambda的输入是已有模型的输出model_body.output和真值y_true,输出是1个值,即损失值。
1 model_loss = Lambda(yolo_loss, output_shape=(1,), name='yolo_loss', 2 arguments={'anchors': anchors, 'num_classes': num_classes, 'ignore_thresh': 0.5})( 3 [*model_body.output, *y_true]) 4 5 model = Model([model_body.input, *y_true], model_loss)
生成一个损失层。
进入yolo_loss内部:
1 def yolo_loss(args, anchors, num_classes, ignore_thresh=.5, print_loss=False):
参数含义:
- args是Lambda层的输入,即model_body.output和y_true的组合;
- anchors是二维数组,结构是(9, 2),即9个anchor box;
- num_classes是类别数;
- ignore_thresh是过滤阈值;
- print_loss是打印损失函数的开关;
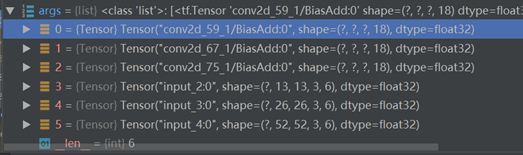
前三个是预测值model_body.output,后三个是真实值y_true。
预测值和真实值分离:
1 num_layers = len(anchors)//3 # default setting 输出层神经元的个数(三个下采样尺度) 2 yolo_outputs = args[:num_layers] # 预测值 3 y_true = args[num_layers:] # 真实值 预测与真实分离, 前三个是真实值,后三个是预测值
输入的维度、网格的维度:
1 anchor_mask = [[6,7,8], [3,4,5], [0,1,2]] if num_layers == 3 else [[3,4,5], [1,2,3]] # 先验框分组 2 input_shape = K.cast(K.shape(yolo_outputs[0])[1:3] * 32, K.dtype(y_true[0])) # 13*13 的宽高回归416*416 3 grid_shapes = [K.cast(K.shape(yolo_outputs[l])[1:3], K.dtype(y_true[0])) for l in range(num_layers)] # 三种尺度的shape 4 loss = 0
模型的batch_size
1 m = K.shape(yolo_outputs[0])[0] # 输入模型的图片总量 2 batch_size mf = K.cast(m, K.dtype(yolo_outputs[0])) # 调整类型
对于每一种尺度进行循环:
- 提取置信度信息
- 提取分类信息
1 for l in range(num_layers): 2 object_mask = y_true[l][..., 4:5] 3 true_class_probs = y_true[l][..., 5:]
通过最后一层的输出,构建pred_box。(?,?,?,3,2 + ?,?,?,3,2 -> ?,?,?,6,2(pred_box))
1 grid, raw_pred, pred_xy, pred_wh = yolo_head(yolo_outputs[l], 2 anchors[anchor_mask[l]], num_classes, input_shape, calc_loss=True) 3 pred_box = K.concatenate([pred_xy, pred_wh]) # 组合成预测框pred_box
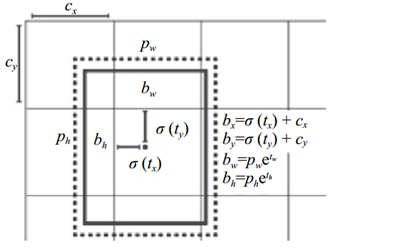
其中,yolo_head的作用是将最后一层的特征转换为b-box的信息,其中,会包含b-box特征的计算:
x, y, 物体置信度以类别置信度部分均经过 Sigmoid 函数激活, 然后采用SSE 计算最终损失。
1 box_xy = (K.sigmoid(feats[..., :2]) + grid) / K.cast(grid_shape[::-1], K.dtype(feats)) 2 box_wh = K.exp(feats[..., 2:4]) * anchors_tensor / K.cast(input_shape[::-1], K.dtype(feats)) 3 box_confidence = K.sigmoid(feats[..., 4:5]) # 框置信度 4 box_class_probs = K.sigmoid(feats[..., 5:]) # 类别置信度
box_xy的计算过程为 将feats中x,y相关的信息sigmoid后(将feats映射到(0,1)), 与所在网格位置加和 再归一化。
grid 相当于是Cx和Cy,即目标中心点所在网格左上角距最左上角相差的格子数。虽然实际过程中,grid是0~12等差分布的(13,13,1,2)的张量,但可以实现上述的需求。(当前的feats为13*13中的)
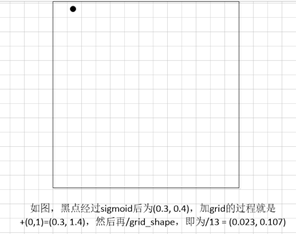
同理,宽高wh:将feats中w,h的值,经过exp正值化,再乘以anchors_tensor的anchor box,再除以图片宽高,(归一化);
因此,返回的box_xy和box_wh是相对于当前小网格相对于大网格的位置。(相对于特征图的位置)
由于在真值的设计中,位置参数是相对于规范化后图片的位置。此时是相对于小网格的位置,所以后续在loss计算中,应该会有尺度的缩放。
由于此时是用于计算损失函数,返回值为
- 网格grid:结构是(13, 13, 1, 2),数值为0~12的全遍历二元组, 包含x和y两层;
- 预测值feats:经过reshape变换,将18维数据分离出3维anchors,结构是(?, 13, 13, 3, 6)
- box_xy和box_wh归一化的起始点xy和宽高wh,xy的结构是(?, 13, 13, 3, 2),wh的结构是(?, 13, 13, 3, 2);box_xy的范围是(0~1),box_wh的范围是(0~1);即bx、by、bw、bh计算完成之后,再进行归一化。 (只有一个类别的情况下 -- 6=5+1)
1 if calc_loss == True: 2 return grid, feats, box_xy, box_wh
有了预测值,便可以进行损失函数的计算。
循环计算每1层的损失值,累加到一起。
1 for l in range(num_layers): 2 ... 3 loss += xy_loss + wh_loss + confidence_loss + class_loss
...部分:
- 生成真实数据
- 根据置信度 生成 二值向量
- 损失的计算
1. 生成真实数据
1 raw_true_xy = y_true[l][..., :2]*grid_shapes[l][::-1] - grid 2 raw_true_wh = K.log(y_true[l][..., 2:4] / anchors[anchor_mask[l]] * input_shape[::-1]) 3 raw_true_wh = K.switch(object_mask, raw_true_wh, K.zeros_like(raw_true_wh)) # avoid log(0)=-inf 4 box_loss_scale = 2 - y_true[l][..., 2:3]*y_true[l][..., 3:4] # 2-box_ares)避免大框的误差对loss 比小框误差对loss影响大
真实框尺度缩放到尺度下的方式。

代码第4行,有w*h越小,则box_loss_scale 越大;
同时w*h越小,其面积(w*h就是面积)就越小,面积越小,在和anchor做比较的时候,iou必然就小,导致"存在物体"的置信度就越小。也就是object_mask越小。
于是,object_mask * box_loss_scale在这里形成了一个制衡条件,这也就是我把box_loss_scale看做一个制衡值的原因。
损失函数的计算是在特征图上的,而不是将其转化至416,416的图上,或者转化到原图上。
# raw_true_xy:在网格中的中心点xy,偏移数据,值的范围是0~1 (相对于一个小格子而言);
果然,在这里会有真实数据的尺度缩放,转化为对于小格子而言的。
# y_true的第0和1位是中心点xy的相对于规范化图片的位置,范围是0~1;
# raw_true_wh:在网络中的wh相对于anchors的比例,再转换为log形式,范围是有正有负;
# y_true的第2和3位是宽高wh的相对于规范化图片的位置,范围是0~1;
# box_loss_scale:计算wh权重,取值范围(1~2);
2. 根据置信度生成二值向量
接着,根据IoU忽略阈值生成ignore_mask,将预测框pred_box和真值框true_box计算IoU
抑制不需要的anchor框的值,即IoU小于最大阈值的anchor框。
ignore_mask的shape是(?, ?, ?, 3, 1),第0位是批次数,第1~2位是特征图尺寸。
并且找一个最大的负责预测该物体
1 ignore_mask = tf.TensorArray(K.dtype(y_true[0]), size=1, dynamic_size=True) 2 object_mask_bool = K.cast(object_mask, 'bool') 3 4 def loop_body(b, ignore_mask): 5 true_box = tf.boolean_mask(y_true[l][b,...,0:4], object_mask_bool[b,...,0]) # 抑制不需要的anchor框 6 iou = box_iou(pred_box[b], true_box) # 计算了iou 7 best_iou = K.max(iou, axis=-1) # 找一个 iou最大的 8 ignore_mask = ignore_mask.write(b, K.cast(best_iou<ignore_thresh, K.dtype(true_box))) #当iou小于阈值时记录,即认为这个预测框不包含物体 9 return b+1, ignore_mask 10 11 _, ignore_mask = K.control_flow_ops.while_loop(lambda b,*args: b<m, loop_body, [0, ignore_mask]) #传入loop_body函数初值为b=0,ignore_mask 12 ignore_mask = ignore_mask.stack() 13 ignore_mask = K.expand_dims(ignore_mask, -1) # 扩展维度用于计算loss
此处box_iou的计算时带中心点坐标的计算,即包含位置的计算,而不是像Kmeans中那样拼在一起的计算。
3. 损失的计算


上述Loss的关于损失的描述应该是最为直接恰当的, 但和代码对比 好像有些不一样。
可以看出,YOLO v3中主要包含三种损失,即坐标的损失,置信度的损失、分类的损失。λobj表示当前的网格中是否存在物体,存在为1,不存在为0。误差采用SSE计算。
1 xy_loss = object_mask * box_loss_scale * K.binary_crossentropy(raw_true_xy, raw_pred[...,0:2], from_logits=True) 2 wh_loss = object_mask * box_loss_scale * 0.5 * K.square(raw_true_wh-raw_pred[...,2:4]) 3 confidence_loss = object_mask * K.binary_crossentropy(object_mask, raw_pred[...,4:5], from_logits=True)+ 4 (1-object_mask) * K.binary_crossentropy(object_mask, raw_pred[...,4:5], from_logits=True) * ignore_mask 5 class_loss = object_mask * K.binary_crossentropy(true_class_probs, raw_pred[...,5:], from_logits=True)
binary_crossentropy和sigmoid的应用(体现在K.binary_crossentropy(raw_true_xy, raw_pred [...,0:2], from_logits=True)),算是非常大胆的了。因为二分类是得到比较"绝对"的输出,非黑即白,非0即1,在链式结构中,非常容易造成"一失足成千古恨"的结果。比如:每次预测值都是0.9,十次以后(0.9的10次方)就非常非常小了。

当真实输出与期望输出接近时,代价函数接近于0.
为了实现多标签分类,模型不再使用softmax函数作为最终的分类器,而是使用logistic作为分类器,使用 binary cross-entropy作为损失函数。

从 Sigmoid 函数的导数图像 (图 6)可以看到, 当神经网络的输出较大时, 会变得非常小, 此时使用平方误差得到的误差值很小, 导致网络收敛很慢, 出现误差越大收敛越慢, 也就是梯度消失的情况。(梯度消失看的是导数的曲线)。 应对该问题,一般会采用交叉熵(从代码中可以看出,使用sigmoid计算的xy, 物体置信度、类别置信度中均使用了交叉熵)
模型最终的损失(取均值)
1 xy_loss = K.sum(xy_loss) / mf 2 wh_loss = K.sum(wh_loss) / mf 3 confidence_loss = K.sum(confidence_loss) / mf 4 class_loss = K.sum(class_loss) / mf 5 loss += xy_loss + wh_loss + confidence_loss + class_loss