暑假考试题7：number（二分+组合数）

题目：

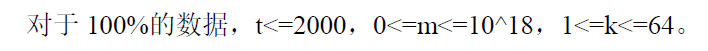
 分析：

题意：求n+1~n*2中恰好有m个二进制有k个1的n，及其个数。

通过打表输出每一个数二进制位下有多少个1可以发现：一个数越大，它对应的区间包含2个1,3个1……的数量越多

也就是说，答案满足单调性，可以二分找到刚好=k个的数（xx=check(mid*2)-check(mid)）。

求解个数：若找到一个最小的n满足条件，那么n+1,n+2……也可能满足条件，所以说满足条件的答案一定是一段连续的区间。

用两个二分，第一次求出最小的n，第二次求出最大的n1，个数即为n~n1这段数。

如何计算一个数有多少个数满足二进制下有k个1？

从低到高for这个数的每一位，如果这一位为1，那么就用组合数计算：0~i-1位中所有位置选（k-cnt）个1的方案数（cnt是已经有了的1）

因为后面的位置中已经有了cnt个1，在剩下的位置上再选几个1凑成k个。（这样就计算出1~n的数中满足条件的数，然后通过相减得到n+1~2*n）

注意：组合数要用杨辉三角的递推初始化，否则会超时或爆long long （1<<x，x即使是小于64也有可能会爆long long！！！）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll inf=(ll) 1 << 62 ;
ll k,c[70][70];
ll quick_pow(ll a,ll k)
{
    ll ans=1;
    while(k){
        if(k&1) ans*=a;
        a*=a; k>>=1;
    }
    return ans;
}
void init()
{
    for(int i=0;i<=63;i++) c[i][0]=1;
    for(int i=1;i<=63;i++)
     for(int j=1;j<=63;j++)
      c[i][j]=c[i-1][j]+c[i-1][j-1];
}
ll check(ll x)
{
    //printf("x:%lld ",x);
    ll tmp=0,cnt=0;
    for(int i=62;i>=0;i--)
     if((x>>i)&1){
         if(k>=cnt) tmp+=c[i][k-cnt];
        cnt++;
    }
    return tmp;
}
int main()
{
    freopen("number.in","r",stdin);
    freopen("number.out","w",stdout);
    int T; ll m;
    scanf("%d",&T);
    init();
    while(T--){
        scanf("%lld%lld",&m,&k);
        if(k==1) { printf("4 -1
"); continue; }
        ll l=1,r=inf,ans1=1,ans2=1;
        while(l<r){
            ll mid=(l+r)>>1,xx=check(mid*2)-check(mid);
            if(xx<m) l=mid+1;
            else if(xx>m) r=mid;
            else ans1=mid,r=mid;
        }
        l=1,r=inf;
        while(l<r){
            ll mid=(l+r)>>1,xx=check(mid*2)-check(mid);
            if(xx<m) l=mid+1;
            else if(xx>m) r=mid;
            else ans2=mid,l=mid+1;
        }
        printf("%lld %lld
",ans1,ans2-ans1+1);
    }
}
/*
3
3 2

4
0 2
1 2
2 2
3 2


*/