LaTex语法

使用LaTex可以生成复杂的数学公式。

举例：

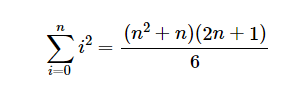
其LaTex语法如下： LaTex具有很强的可读性，例如 sum 表示求和，多练练就能掌握。

 sum_{i=0}^n i^2 = frac{(n^2+n)(2n+1)}{6} 

 LaTex目前已经成为“数理化”的行业的标准语法。因此，你不用担心学会了在其他系统里无法使用。

在word里，你也可以用LaTex语法写公式。

　　

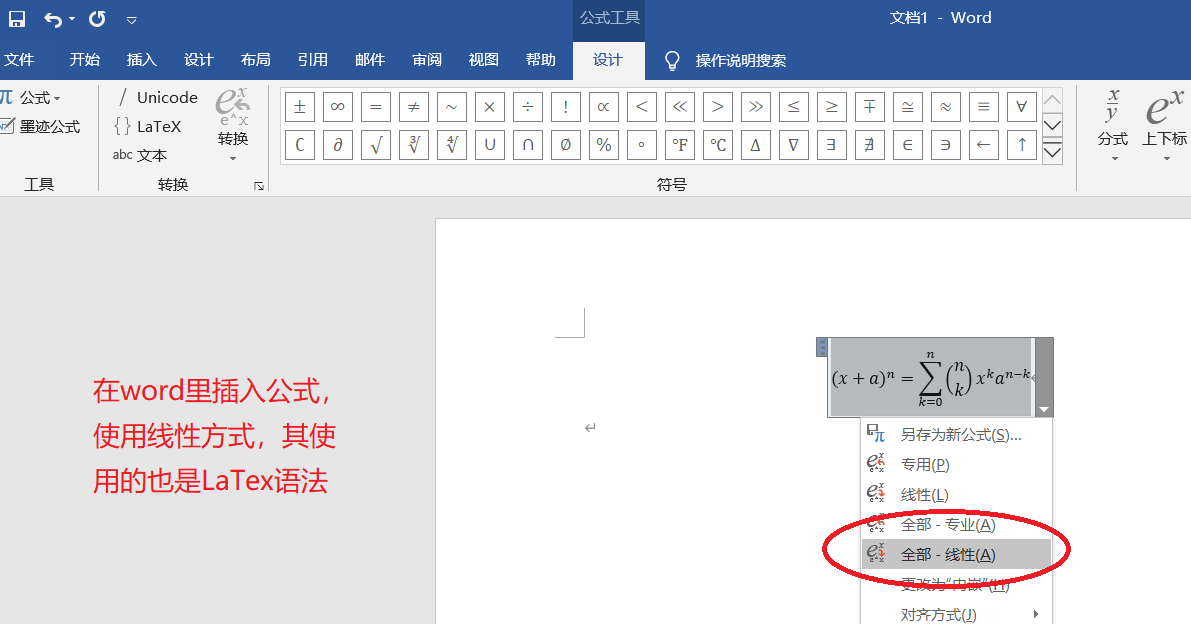
对于部分公式，需要注意：换行。这是因为，部分公式行较高，如果采用行内元素，可能显示错误，请勾选“换行”

 frac{partial u}{partial t}
   = h^2 left( frac{partial^2 u}{partial x^2}
      + frac{partial^2 u}{partial y^2}
      + frac{partial^2 u}{partial z^2} 
ight)  

　　

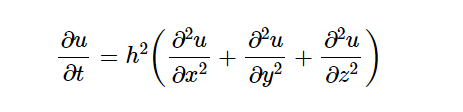
 举例2：

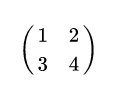
egin{pmatrix}1&2\3&4\ end{pmatrix}

　　

 

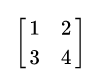
egin{bmatrix}1&2\3&4\ end{bmatrix}

　　

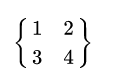
egin{Bmatrix}1&2\3&4\ end{Bmatrix}

　　

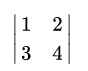
egin{vmatrix}1&2\3&4\ end{vmatrix}

　　

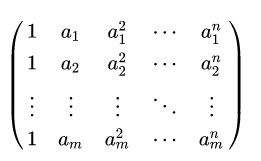
egin{pmatrix}
 1 & a_1 & a_1^2 & cdots & a_1^n \
 1 & a_2 & a_2^2 & cdots & a_2^n \
 vdots  & vdots& vdots & ddots & vdots \
 1 & a_m & a_m^2 & cdots & a_m^n    
 end{pmatrix}

　　

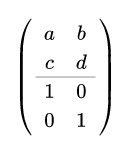
egin{pmatrix}
    a & b\
    c & d\
  hline
    1 & 0\
    0 & 1
  end{pmatrix}

　　

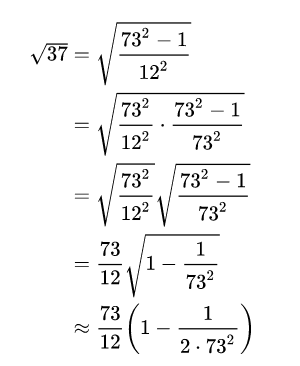
egin{align}
sqrt{37} & = sqrt{frac{73^2-1}{12^2}} \
 & = sqrt{frac{73^2}{12^2}cdotfrac{73^2-1}{73^2}} \ 
 & = sqrt{frac{73^2}{12^2}}sqrt{frac{73^2-1}{73^2}} \
 & = frac{73}{12}sqrt{1 - frac{1}{73^2}} \ 
 & approx frac{73}{12}left(1 - frac{1}{2cdot73^2}
ight)
end{align}

　　

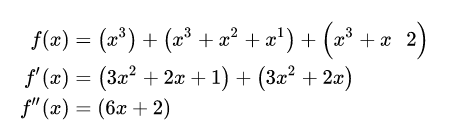
egin{align} f(x)&=left(x^3
ight)+left(x^3+x^2+x^1
ight)+left(x^3+x^‌​2
ight)\ f'(x)&=left(3x^2+2x+1
ight)
+
left(3x^2+2x
ight)\ f''(x)&=left(6x+2
ight)\ end{align}

　　

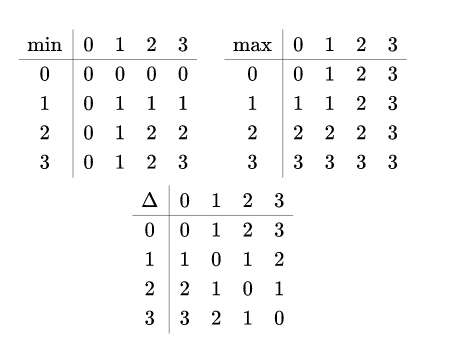
% outer vertical array of arrays
egin{array}{c}
% inner horizontal array of arrays
egin{array}{cc}
% inner array of minimum values
egin{array}{c|cccc}
	ext{min} & 0 & 1 & 2 & 3\
hline
0 & 0 & 0 & 0 & 0\
1 & 0 & 1 & 1 & 1\
2 & 0 & 1 & 2 & 2\
3 & 0 & 1 & 2 & 3
end{array}
&
% inner array of maximum values
egin{array}{c|cccc}
	ext{max}&0&1&2&3\
hline
0 & 0 & 1 & 2 & 3\
1 & 1 & 1 & 2 & 3\
2 & 2 & 2 & 2 & 3\
3 & 3 & 3 & 3 & 3
end{array}
end{array}
\
% inner array of delta values
egin{array}{c|cccc}
Delta&0&1&2&3\
hline
0 & 0 & 1 & 2 & 3\
1 & 1 & 0 & 1 & 2\
2 & 2 & 1 & 0 & 1\
3 & 3 & 2 & 1 & 0
end{array}
end{array}

　　

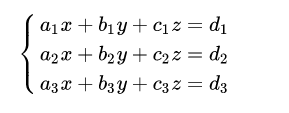
left{ 
egin{array}{c}
a_1x+b_1y+c_1z=d_1 \ 
a_2x+b_2y+c_2z=d_2 \ 
a_3x+b_3y+c_3z=d_3
end{array}

ight.

　　

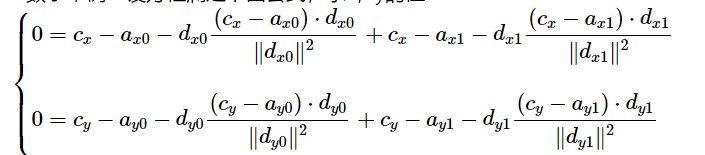
 left{ egin{array}{l}
0 = c_x-a_{x0}-d_{x0}dfrac{(c_x-a_{x0})cdot d_{x0}}{|d_{x0}|^2} + c_x-a_{x1}-d_{x1}dfrac{(c_x-a_{x1})cdot d_{x1}}{|d_{x1}|^2} \[2ex] 
0 = c_y-a_{y0}-d_{y0}dfrac{(c_y-a_{y0})cdot d_{y0}}{|d_{y0}|^2} + c_y-a_{y1}-d_{y1}dfrac{(c_y-a_{y1})cdot d_{y1}}{|d_{y1}|^2} end{array} 
ight.