以二叉链表来作为储存结构的时候,只能找到左右孩子的信息,不能直接得到结点的前驱和后继信息,这种信息只有在遍历的过程中才能实现。在n个结点的二叉链表中必定存在n+1个空链域。可以用这些空链域来保存这些信息;做以下规定:若结点有左子树,则lchild指向其左孩子,若没有左孩子则指向其前驱;若结点有右子树,则rchild指向其右子树,否则指向其后继;为了标志指针是线索还是指针,需要添加两个标志位来表示指针的性质
| lchild | LTag | rchild | RTag |
LTag,RTag是枚举类对象, 值为0的时候表示指针, 值为1表示线索
1 typedef enum PointerTag{Link, Thread};
当我们能知道结点的前驱和后继信息的时候,只要找到序列中的第一个结点,然后依次查找后继结点,直到后继为空时而止;
怎么在二叉树中求结点的后继信息?
对于右孩子为空的结点来说,其右孩子指针指向其后继。但是当结点的右孩子不为空的时候,怎么找到其后继信息?根据后序遍历的规定可以直到,结点的后继结点应该是遍历其右子树最左下角的结点。当结点的左孩子为空的时候,左孩子指针指向其前驱, 当左孩子不为空的时候, 结点的前驱是遍历左子树的最后一个结点,也就是左子树最右下角的结点;(这些都是针对中序遍历而言)
对线索树的结点做一下定义, 为了简便,结点类型用int类型
1 typedef struct BiThrNode{ 2 int val; 3 struct BiThrNode *lchild, *rchild; 4 PointerTag LTag, RTag; 5 }BiThrNode, *BiThrTree;
对二叉树进行线索化:pre是上一个访问的结点,pre的初始值指向表头结点(即后面的Thrt,其左孩子指向根节点); 线索化的过程是一个从叶子结点到根节点的过程,从左子树到右子树的过程;根据上面的分析可以知道,当一个结点的孩子为null的时候,就指向前驱或者后继。 调用这个函数后除最后一个结点,结点的指针都指向孩子结点或者前驱后继。
1 void InThreading(BiThrTree p, BiThrTree& pre){ 2 if(p){ 3 InThreading(p->lchild, pre); //左子树线索化 4 if(!p->lchild){ //p左孩子为null,则指向pre,指向p的前驱 5 p->LTag = Thread; 6 p->lchild = pre; 7 }else p->LTag = Link; 8 if(!pre->rchild){ //pre右孩子为null,则指向p,表示p是pre的后驱 9 pre->RTag = Thread; 10 pre->rchild = p; 11 }else pre->RTag = Link; 12 pre = p; //更新p的位置 13 InThreading(p->rchild, pre); //右子树线索化 14 } 15 }
建立一个循环到线索树:Thrt是一个头结点,左孩子指向根节点, 右孩子指向树的最后一个结点。又让树的最后一个结点右孩子指向Thrt。这样就构成一个循环的线索树。当对树进行中序遍历的时候,若某一个结点的右孩子指向Thrt,则表示遍历完成
1 void InOrderThreading(BiThrTree& Thrt, BiThrTree& T){ 2 Thrt = (BiThrNode*) malloc(sizeof(BiThrNode)); 3 Thrt->LTag = Link; Thrt->RTag = Thread; 4 Thrt->rchild = Thrt; 5 BiThrTree pre; 6 if(!T) Thrt->lchild = Thrt; 7 else{ 8 Thrt->lchild = T; 9 pre = Thrt; 10 InThreading(T, pre); //中序遍历线索化 11 pre->rchild = Thrt; pre->RTag = Thread; //最后一个结点线索化 12 Thrt->rchild = pre; 13 } 14 }
根据线索树进行中序遍历:由上面的分析可以写出下面的中序遍历程序,先找到要遍历的第一个结点,在中序遍历中,即数的最左下角的结点。找到第一个结点后就根据当前节点的后继结点来进行遍历;当结点的右孩子指针不指向后继节点的时候,这继续访问当前结点的右子树(由中序遍历先遍历左子树可以知道, 当访问的结点有右孩子的时候,其右孩子一定已经访问完成),重复上面的过程就遍历所有的结点
1 void InOrderTraverse(BiThrTree Thrt){ 2 BiThrNode *p = Thrt->lchild; //让p指向树的根节点 3 while(p!=Thrt){ 4 while(p->LTag==Link) p = p->lchild; //指向树的最左下方 5 cout<<p->val<<" "; 6 while(p->RTag==Thread && p->rchild!=Thrt){ //根据后继结点进行遍历 7 p = p->rchild; 8 cout<<p->val<<" "; 9 } //接待右孩子不为空的时候,退出循环,继续访问当前结点的右子树 10 p = p->rchild; // 11 } 12 cout<<endl; 13 }
在将二叉树线索化之前,需要建立一个二叉树,这里通过递归的方式来建立一棵树
1 BiThrTree CreateBiTree(BiThrTree T, int val){ 2 if(!T){ 3 T = (BiThrNode*) malloc(sizeof(BiThrNode)); 4 T->val = val; 5 T->lchild = T->rchild = NULL; 6 return T; 7 } 8 if(val<T->val) T->lchild = CreateBiTree(T->lchild, val); 9 if(val>T->val) T->rchild = CreateBiTree(T->rchild, val); 10 return T; 11 }
完整代码
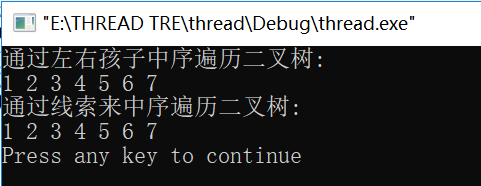
把数的结点信息按照,层序遍历的顺序储存在数组t之中,建立通过CreateBiTree()建立二叉树, 再通过inorder()来验证二叉树建立是否正确,这里给出的例子,如果建立二叉树正确,二叉遍历的结果应该是一个从1到7的升序数列; 然后验证上面的线索二叉树的构造过程是否正确,先通过InorderThreading来将二叉树线索化, 然后再通过InorderTrverse()来验证;
1 #include<iostream> 2 using namespace std; 3 /* 4 author: Lai XingYu 5 date: 2018/5/18 6 describe: threaded binary tree 7 */ 8 9 typedef enum PointerTag{Link, Thread}; //标志指针类型,前者表示指针, 后者表示线索 10 typedef struct BiThrNode{ 11 int val; 12 struct BiThrNode *lchild, *rchild; 13 PointerTag LTag, RTag; 14 }BiThrNode, *BiThrTree; 15 16 /* 17 对二叉树线索化, pre表示上一个访问的结点 18 */ 19 void InThreading(BiThrTree p, BiThrTree& pre){ 20 if(p){ 21 InThreading(p->lchild, pre); //左子树线索化 22 if(!p->lchild){ //p左孩子为null,则指向pre,指向p的前驱 23 p->LTag = Thread; 24 p->lchild = pre; 25 }else p->LTag = Link; 26 if(!pre->rchild){ //pre右孩子为null,则指向p,表示p是pre的后驱 27 pre->RTag = Thread; 28 pre->rchild = p; 29 }else pre->RTag = Link; 30 pre = p; //更新p的位置 31 InThreading(p->rchild, pre); //右子树线索化 32 } 33 } 34 35 /* 36 Thr是头结点, 其左孩子指向根节点, 右孩子指向树的最后一个结点 37 树的最后一个结点的右孩子指向THr,构成一个回环 38 */ 39 void InOrderThreading(BiThrTree& Thrt, BiThrTree& T){ 40 Thrt = (BiThrNode*) malloc(sizeof(BiThrNode)); 41 Thrt->LTag = Link; Thrt->RTag = Thread; 42 Thrt->rchild = Thrt; 43 BiThrTree pre; 44 if(!T) Thrt->lchild = Thrt; 45 else{ 46 Thrt->lchild = T; 47 pre = Thrt; 48 InThreading(T, pre); //中序遍历线索化 49 pre->rchild = Thrt; pre->RTag = Thread; //最后一个结点线索化 50 Thrt->rchild = pre; 51 } 52 } 53 54 void InOrderTraverse(BiThrTree Thrt){ 55 BiThrNode *p = Thrt->lchild; //让p指向树的根节点 56 while(p!=Thrt){ 57 while(p->LTag==Link) p = p->lchild; //指向树的最左下方 58 cout<<p->val<<" "; 59 while(p->RTag==Thread && p->rchild!=Thrt){ 60 p = p->rchild; 61 cout<<p->val<<" "; 62 } 63 p = p->rchild; 64 } 65 cout<<endl; 66 } 67 68 BiThrTree CreateBiTree(BiThrTree T, int val){ 69 if(!T){ 70 T = (BiThrNode*) malloc(sizeof(BiThrNode)); 71 T->val = val; 72 T->lchild = T->rchild = NULL; 73 return T; 74 } 75 if(val<T->val) T->lchild = CreateBiTree(T->lchild, val); 76 if(val>T->val) T->rchild = CreateBiTree(T->rchild, val); 77 return T; 78 } 79 80 void inorder(BiThrTree T){ 81 if(!T) return; 82 if(T->lchild) inorder(T->lchild); 83 cout<<T->val<<" "; 84 if(T->rchild) inorder(T->rchild); 85 } 86 87 int main(){ 88 int t[] = {4,2,5,1,3,6,7}, i; 89 BiThrTree T = NULL, Thrt; 90 for(i=0; i<7; i++) T = CreateBiTree(T, t[i]); 91 inorder(T); 92 cout<<endl; 93 InOrderThreading(Thrt, T); 94 InOrderTraverse(Thrt); 95 return 0;}
在准备408考试的时候接触到这个线索二叉树,理解还是有些吃力;不能理解的是,这样的储存结构的意义在哪里?就算保存了前驱后继信息,也到先找到该节点, 此外,根据实现的过程来看, 当二叉树建立之后, 若要插入新的节点又要重新对二叉树进行线索化, 这个开销也是不小的
后序线索树的构造
后序线索树的构造比,中序线索树更为复杂,可以分为以下四种情况
- 如果节点为根节点,则后继结点为空
- 结点是双亲的右孩子,或者是左孩子且没有兄弟结点, 则后继结点是双亲结点
- 结点为双清结点的左孩子,且有兄弟结点,则后继结点双亲右子树按照后序遍历的第一个结点。
- 结点为双亲的右孩子,后继为双亲结点