[HNOI2007]最小矩形覆盖

嘟嘟嘟


这道题我从昨天晚上5点做到今天下午3点半……差点就疯了。
真是一道计算几何好题呀！？


刚开始我以为矩形与坐标轴平行，感觉省选题竟然这么水。但是看完样例后发现我错了……


首先都知道要求凸包。写代码的时候一定要非常谨慎。对于重合或共线的点都要从栈中弹去，否则在后面的求矩形面积的时候会除以(0)，然后就会想我一样(gg)了快(2)个点。
然后，凭直觉能知道矩形的一个边一定和凸包的一条边平行。那么就能想到用旋转卡壳维护矩形的另外三个最值点（不是顶点），即矩形最上点，最右点，最左点。
求最上点，和旋转卡壳板子一样，用叉积求面积就行了。
求最右点，用点积。对于当前直线(AB)和旋转到的点(Ci)，如果(overrightarrow{AB} * overrightarrow{C _ i C_{i + 1}} > 0)，就接着往下旋转。
求最左点，和最右点同理。只不过判断条件是(< 0)。而且他的旋转方向和上面相反，所以我又倒着跑了一遍旋转卡壳。


接下来说怎么求面积。

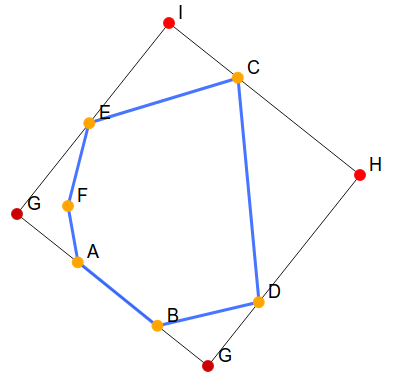
看这个图就好了。
首先矩形的宽很好求，就是(Delta ABC)以(AB)为底边的高。用叉积求一遍面积然后除以底边长完事。
然后求矩形的底边长。我是把他分成了三部分：令(a)表示(AB)的长度，(b)表示(overrightarrow{BD})在(overrightarrow{AB})上的投影，(c)表示(overrightarrow{AE})在(overrightarrow{AB})上的投影，则底边长(l = |a| + |b| + |c|)。
所以面积求完了啦！


最后是怎么求矩形的四个顶点。
沿用上面的字母。
思路是从右下点(G)开始逆时针一次求。
(G = B + overrightarrow{AB} * frac{|overrightarrow{BG}|}{|overrightarrow{AB}|})。
接下来求(H)。原来我是这么求的：(H = G + overrightarrow{GD} * frac{|overrightarrow{GH}|}{|overrightarrow{GD}|})。但是会有(G, D)重合的情况。所以就换了种求法，把(overrightarrow{AB})顺时针旋转(90)度得到(overrightarrow{BA'})，然后(H = G + overrightarrow{BA'} * (- frac{|overrightarrow{GH}|}{|overrightarrow{BA'}|}))，其中({|overrightarrow{GH}|})就是矩形的高，上一问已经求过。
对于(I, G)同理，都是向量旋转加伸长缩短，这里就不讲了。
好像就做完了……
感觉写了一天的题也不怎么难。还是自己菜啊……


需要注意的是这题卡精度，(eps)开到(1e-10)我才过。然后如果(|a| < 1e-5)，直接输出(0.00000)，否则可能会输出(-0.00000)……

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("") 
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define rg register
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-10;
const int maxn = 5e4 + 5;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}

int n;
struct Point
{
  db x, y; int id;     //id跟题目无关,是为了方便调试用的
  Point operator - (const Point& oth)const
  {
    return (Point){x - oth.x, y - oth.y, 0};
  }
  Point operator + (const Point& oth)const
  {
    return (Point){x + oth.x, y + oth.y, 0};
  }
  db operator * (const Point& oth)const
  {
    return x * oth.y - oth.x * y;
  }
  db operator ^ (const Point& oth)const  //这是点积,不是位运算……
  {
    return x * oth.x + y * oth.y;
  }
  Point operator * (db d)
  {
    return (Point){x * d, y * d, 0};
  }
  friend inline db dis(const Point& A)
  {
    return A.x * A.x + A.y * A.y;
  }
  friend inline Point rot(const Point& A)    //顺时针旋转90度
  {
    return (Point){A.y, -A.x};
  }
}p[maxn], S;

bool cmp(Point& A, Point& B)
{
  db s = (A - S) * (B - S);
  if(fabs(s) > eps) return s > eps;
  return dis(A - S) < dis(B - S) - eps;
}
int st[maxn], top = 0;
void Graham()
{
  int id = 1;
  for(int i = 2; i <= n; ++i)
    if(p[i].x < p[id].x - eps || (fabs(p[i].x - p[id].x) < eps && p[i].y < p[id].y - eps)) id = i;
  if(id != 1) swap(p[id].x, p[1].x), swap(p[id].y, p[1].y), swap(p[id].id, p[1].id);
  S.x = p[1].x, S.y = p[1].y;
  sort(p + 2, p + n + 1, cmp);
  st[++top] = 1;
  for(int i = 2; i <= n; ++i)
    {
      while(top > 1 && (p[st[top]] - p[st[top - 1]]) * (p[i] - p[st[top - 1]]) < eps) top--;
      st[++top] = i;
    }
}

struct Rec
{
  Point R, U, L;
}r[maxn];
db area(Point A, Point B, Point C)
{
  return (B - A) * (C - A);
}
db pho(Point A, Point B, Point C, Point D)
{
  return (B - A) ^ (D - C);
}
inline int nxt(int x)
{
  if(++x > top) x = 1;
  return x;
}
void rota1()
{
  for(int i = 1, j = 3, k = 2; i <= top; ++i)
    {
      while(nxt(j) != i && area(p[st[i]], p[st[i + 1]], p[st[j]]) < area(p[st[i]], p[st[i + 1]], p[st[nxt(j)]]) - eps) j = nxt(j);
      r[i].U = p[st[j]];
      while(nxt(k) != i && pho(p[st[i]],  p[st[i + 1]], p[st[k]], p[st[nxt(k)]]) > eps) k = nxt(k);
      r[i].R = p[st[k]];
    }
}
inline int pre(int x)
{
  x--;
  if(!x) x = top;
  return x;
}
void rota2()   //单独维护最左点
{
  for(int i = top, j = top; i; --i)
    {
      while(pre(j) != i + 1 && pho(p[st[i]], p[st[i + 1]], p[st[j]], p[st[pre(j)]]) < eps) j = pre(j);
      r[i].L = p[st[j]];
    }
}

Point Ans[5];

int main()
{
  n = read();
  for(int i = 1; i <= n; ++i) scanf("%lf%lf", &p[i].x, &p[i].y);
  for(int i = 1; i <= n; ++i) p[i].id = i;
  Graham(); st[top + 1] = st[1];
  rota1(); rota2();
  db ans = (db)INF * (db)INF;
  for(int i = 1; i <= top; ++i)
    {
      //printf("Line:%d %d R:%d U:%d L:%d
", p[st[i]].id, p[st[i + 1]].id, r[i].R.id, r[i].U.id, r[i].L.id);
      Point AB = p[st[i + 1]] - p[st[i]];
      db a = sqrt(dis(AB));
      db b = (AB ^ (r[i].L - p[st[i]])) / a, c = (AB ^ (r[i].R - p[st[i + 1]])) / a;
      b = fabs(b), c = fabs(c);
      db l = a + b + c;
      db h = AB * (r[i].U - p[st[i]]) / a;
      h = fabs(h);
      db s = l * h;
      //printf("**%.3lf %.3lf %.3lf %.3lf %.3lf", a, b, c, l, h);
      //printf("@%.3Lf
", s);
      if(s < ans - eps)
	{
	  ans = s;
	  Ans[0] = p[st[i + 1]] + AB * (c / a);
	  Ans[1] = Ans[0] + rot(AB) * (-h / a);
	  Ans[2] = Ans[1] + rot(Ans[1] - Ans[0]) * (-l / h);
	  Ans[3] = Ans[2] + rot(Ans[2] - Ans[1]) * (-h / l);
	  /*Ans[1] = Ans[0] + (r[i].R - Ans[0]) * (h / dis(Ans[0] - r[i].R));  //这就是我原来的写法，点重合会$gg$
	  Ans[2] = Ans[1] + (r[i].U - Ans[1]) * (l / dis(r[i].U - Ans[1]));
	  Ans[3] = Ans[2] + (r[i].L - Ans[2]) * (h / dis(r[i].L - Ans[2]));*/
	}
    }
  printf("%.5lf
", ans);
  int id = 0;
  for(int i = 1; i < 4; ++i)
    if(Ans[i].y < Ans[id].y - eps || (fabs(Ans[i].y - Ans[id].y) < eps && Ans[i].x < Ans[id].x - eps)) id = i;
  for(int i = 0; i < 4; ++i)
    {
      db x = Ans[(id + i) % 4].x, y = Ans[(id + i) % 4].y;
      if(fabs(x) < 1e-5) x = 0;
      if(fabs(y) < 1e-5) y = 0;
      printf("%.5lf %.5lf
", x, y);
    }
  return 0;
}