传送门
题意:给你一张(n)个点,(m)条边的有向图,每条边有两个权值(a_i)和(b_i),对于一条路径(e_1,e_2,cdots,e_k),每条边的长度是这样计算的:
- (e_1)的长度是(a_{e_1});
- 对于边(e_i(i>1)),如果(a_{e_i} > a_{e_{i-1}}),那么长度为(a_{e_i} - b_{e_i}),否则为(a_{e_i})。
求节点(1)到其他点的最短路。((2 leqslant n leqslant 10^5, 1leqslant m leqslant 2 imes 10^5,a_i > b_i))
这个是ccpc2021网络赛重赛的1009题,比赛上拿线段树+最短路乱搞,tle了。
感觉图论的很多题都是在考建图,建出正确的图后,跑一个比较裸的图论算法就过了。至于原因,我也不是很清楚,总之得有这么个意识吧。
首先的一点在于,一条边两种边权不好整,就拆成两条边权分别只有(a_i)和(a_i-b_i)的边。边权为(a_i)的边任何情况下都可以走,因为最优解一定比全走(a_i)的边优,而走(a_i-b_i)的边需要满足一定的条件。那现在问题在于如何建图,使其当且仅当满足条件时,才会走(a_i-b_i)的边。
考虑拆点。一种暴力的拆点方法是将点(u)拆成(u)的出度个,对于每个拆开的点(u_i),考虑哪些入边能接下来走(a_{u_i} - b_{u_i}).那么这一定是所有满足(a_v < a_{u_i})的入边,于是将这些边连到(u_i)上。但这样连边的复杂度特别高,要想办法优化。
观察到这个条件是有单调性的,即如果(a_v < a_{u_i}),那么对于所有(a_{u_j} geqslant a_{u_i})的边,必然也能满足要求。因此我们可以把所有点按出边边权从大到小排序,对于一条入边(a_{v}),只向(u_i(a_{u_i} > a_v extrm{且最小}))连边,而(u)内部,从(u_i)向(u_{i+1})连一条边权为(0)的边。
这里借用官方题解的图:
原来是这样的:
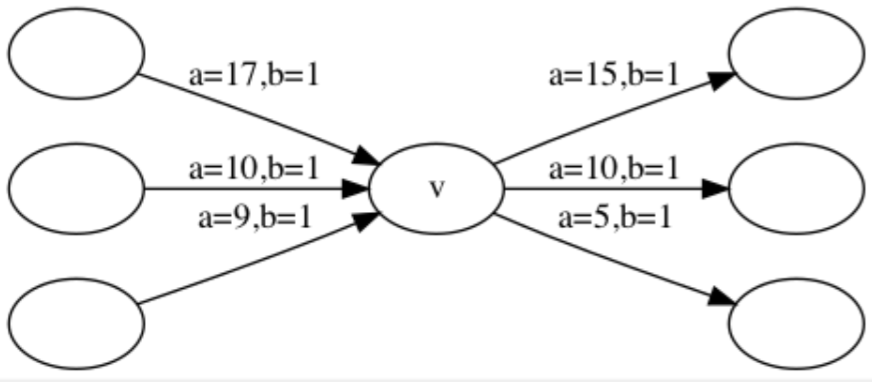
优化后就变成了这样:

这样拆点后总点数(n+m),总边数(3m),用dijkstra的时间复杂度(O(mlog n)).
赛后因为数组越界发生了非常奇怪的错误,debug了半天……
#include<bits/stdc++.h>
using namespace std;
#define enter puts("")
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define In inline
#define forE(i, x, y) for(int i = head[x], y; ~i && (y = e[i].to); i = e[i].nxt)
typedef long long ll;
typedef double db;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const db eps = 1e-8;
const int maxn = 3e5 + 5;
const int maxe = 6e5 + 5;
In ll read()
{
ll ans = 0;
char ch = getchar(), las = ' ';
while(!isdigit(ch)) las = ch, ch = getchar();
while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
if(las == '-') ans = -ans;
return ans;
}
In void write(ll x)
{
if(x < 0) x = -x, putchar('-');
if(x >= 10) write(x / 10);
putchar(x % 10 + '0');
}
In void MYFILE()
{
#ifndef mrclr
freopen("random.in", "r", stdin);
freopen("ac.out", "w", stdout);
#endif
}
int n, m;
struct edges
{
int to, a, b;
In bool operator < (const edges& oth)const
{
return a < oth.a || (a == oth.a && b < oth.b);
}
};
vector<edges> E[maxn];
int sumd[maxn];
In int num(int x, int p) {return sumd[x - 1] + p + 1;}
struct Edge
{
int nxt, to, w;
}e[maxe];
int head[maxn], ecnt = -1;
In void addEdge(int x, int y, int w)
{
e[++ecnt] = (Edge){head[x], y, w};
head[x] = ecnt;
}
bool in[maxn];
ll dis[maxn];
#define pr pair<ll, int>
#define mp make_pair
#define F first
#define S second
In void dijkstra(int s)
{
priority_queue<pr, vector<pr>, greater<pr> > q;
dis[s] = 0;
q.push(mp(dis[s], s));
while(!q.empty())
{
int now = q.top().S; q.pop();
if(in[now]) continue;
in[now] = 1;
forE(i, now, v)
{
if(dis[v] > dis[now] + e[i].w)
{
dis[v] = dis[now] + e[i].w;
q.push(mp(dis[v], v));
}
}
}
}
In void init()
{
ecnt = -1;
for(int i = 1; i <= n + m; ++i)
{
E[i].clear();
head[i] = -1;
dis[i] = INF, in[i] = 0;
}
}
int main()
{
// MYFILE();
int T = read();
while(T--)
{
n = read(), m = read();
init();
for(int i = 1; i <= m; ++i)
{
int x = read(), y = read(), a = read(), b = read();
E[x].push_back((edges){y, a, b});
}
for(int i = 1; i <= n; ++i)
{
sumd[i] = sumd[i - 1] + E[i].size() + 1;
sort(E[i].begin(), E[i].end());
}
for(int i = 1; i <= n; ++i)
{
int siz = E[i].size();
if(siz) addEdge(num(i, siz - 1), num(i, siz), 0);
for(int j = 0; j < siz; ++j)
{
if(j) addEdge(num(i, j - 1), num(i, j), 0);
int v = E[i][j].to;
int pos = upper_bound(E[v].begin(), E[v].end(), (edges){0, E[i][j].a, (int)1e9}) - E[v].begin();
addEdge(num(i, j), num(v, pos), E[i][j].a - E[i][j].b);
addEdge(num(i, siz), num(v, pos), E[i][j].a);
}
}
dijkstra(sumd[1]);
for(int i = 1; i <= n; ++i)
{
ll Min = INF;
for(int j = 0; j <= (int)E[i].size(); ++j) Min = min(Min, dis[num(i, j)]);
write(Min == INF ? -1 : Min), (i == n ? enter : space);
}
}
return 0;
}