无重复元素的全排列
输入n(<=11),按从小到大输出数字1 到n 个的全部排列。
样例:
输入:
3
输出:
1:1 2 3
2:1 3 2
3:2 1 3
4:2 3 1
5:3 1 2
6:3 2 1
全排列可以用STL来写,但为了强化dfs,就用 dfs 吧。
看了某一个pdf,我对搜索有了一个更深的认识。就是关于如何去dfs,我认为可以从这两方面想:一是能否转化为图的问题,二是能否画出搜索树。只要这两种有一个能想出来,那么dfs就一定能写出来。
而能否转化成图的这类题目,一般元素都是固定的,也就是说,图上的结点就固定了。就比如说这个全排列,元素就是1到n固定不变,那么这1到n个数就可以转化成图上的n个结点,其中每两个点之间都连一条边,然后不重复的遍历所有的点就行了。
既然这个图都能想出来,那搜索树就一定能画出来了,这里就不讲了。
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 #define rep(i, a, n) for(int i = a; i <= n; ++i) 8 #define per(i, n, a) for(int i = n; i >= a; --i) 9 typedef long long ll; 10 int n, ans[15], tot = 0; 11 int vis[15]; 12 void print(int x) 13 { 14 printf("%d:", x); 15 rep(i, 1, n) printf("%d ", ans[i]); printf(" "); 16 } 17 void solve(int x, int step) 18 { 19 ans[step] = x; vis[x]= 1; 20 if(step == n) print(++tot); 21 rep(i, 1, n) 22 { 23 if(!vis[i]) 24 { 25 solve(i, step + 1); 26 vis[i] = 0; 27 } 28 } 29 } 30 31 int main() 32 { 33 // freopen("p1.in", "r", stdin); 34 // freopen("p1.out", "w", stdout); 35 scanf("%d", &n); 36 rep(i, 1, n) //从每一个结点出发,遍历方式都不同 37 { 38 memset(vis, 0, sizeof(vis)); 39 solve(i, 1); 40 } 41 return 0; 42 }
有重复元素的全排列
输入n(<=10)个小些字母(可能重复),按从小到大输出输出n 个字符的全部排列。
样例:
输入:
abaab
输出:
1:aaabb
2:aabab
3:aabba
4:abaab
5:ababa
6:abbaa
7:baaab
8:baaba
9:babaa
10:bbaaa
这道题跟全排列相比,元素可以重复。如果全排列方式建图的话,比如下图
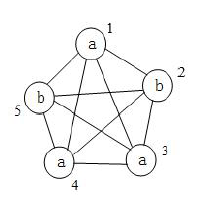
会发现从1,3,4结点出发点的边,遍历的结果是一样的,从2和5出发也是一样。所以对于同一个字母,我们只希望从该点出发一次。
用vis数组标记共字母种类n,然后遍历n次
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 #define rep(i, a, n) for(int i = a; i <= n; ++i) 8 #define per(i, n, a) for(int i = n; i >= a; --i) 9 typedef long long ll; 10 int tot = 0, len; 11 char a[15], ans[15]; 12 int vis[500]; 13 void print(int tot) 14 { 15 printf("%d:%s ", tot, ans + 1); 16 } 17 void dfs(int x) 18 { 19 if(x == len + 1) print(++tot); 20 rep(i, 'a', 'z') 21 { 22 if(vis[i]) //存在这个点 23 { 24 ans[x] = i; 25 vis[i]--; //表示这个点已经走过 26 dfs(x + 1); 27 vis[i]++; 28 } 29 } 30 } 31 int main() 32 { 33 // freopen("p3.in", "r", stdin); 34 // freopen("p3.out", "w", stdout); 35 scanf("%s", a); 36 len = strlen(a); 37 sort(a, a + len); 38 rep(i, 0, len - 1) vis[a[i]]++; 39 dfs(1); 40 return 0; 41 }