计算机中数的表示

注：主要说明整数和浮点数的表示方法。

参考资料：《计算机组成原理》（第2版 唐朔飞 著 ） 以及北航计算机组成原理课件。

1 无符号数和有符号数

无符号数：所有位都是数值位，没有符号位；

有符号数：编码最高位为符号位，“0”表示“正数”，“1”表示“负数”。

2 定点小数和定点整数

（1）定点小数：绝对值小于1；

例如：十进制的0.75，表示为二进制为01100000

转换的规则，可参考百度问答：https://zhidao.baidu.com/question/1836447347903048020.html

我们规定总长度为7位，接着依次计算：
0.75*2=1.5 整数1，小数部分为0.5，继续转换；
0.5*2=1.0  整数1，小数部分为0，转换完毕；
0.75d=0.11b=0.1100000b，低位添0补充到8位。

（2）定点整数：没有小数部分；

整数的十进制和二进制转换就用除基取余法就可以了，就不再解释了。

3 原码、反码、补码

但用符号位和数值位来表示数值时，可用原码、反码、补码表示方式。它们的表示范围如下：

以-3为例进行说明

原码：1000 0011 = 128 + 3
反码：1111 1100 = 255 - 3
补码：1111 1101 = 256 - 3 

4  浮点数的表示

（1）浮点数在机器中的表示

形式如下，由阶码和尾数两部分组成：

阶码：定点整数表示，阶码和阶符的位数m合起来欢迎浮点数的表示范围以及小数点的实际位置。

尾数：定点小数表示，其位数n反应浮点数的精度。

数符：表示浮点数的正负。

举例进行说明：178.125d = 10110010.001b = 0.10110010001×2⁰¹⁰⁰⁰

阶码：01000

尾数：0.10110010001

简单说一下计算过程：

178d = ‭‭‭10110010‬

0.125d = 0.001b

‬‬178.125d = 10110010‬.001b，左移8位，相当于0.10110010001乘以2⁰¹⁰⁰⁰。

（2）IEEE 754标准

 现代计算机，浮点数一般采用IEEE标准，标准形式如下：

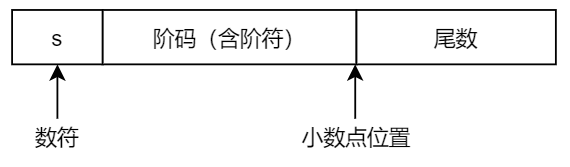
数符s：表示浮点数的正负。

阶码：阶码的真值都被加上一个常数（偏移量），如短实数、长实数的偏移量用十六进制表示为：7FH、3FFH。

尾数：常用规格化表示，即非“0”的有效位最高位总是“1”。

常用的浮点数有：

 举例进行说明：

至此，计算机中数的表示基本说完了。