动态规划整理（斐波那契数列题型全解）（C++实现）

509.斐波那契数

 题解1：（暴力递归）

class Solution {
public:
    int fib(int n) {
        if(n==0) return 0;
        if(n==1) return 1;
        return fib(n-1)+fib(n-2);
    }
};

题解2：（备忘录）

class Solution {
public:

    vector<int>& memo(vector<int>& note, int n){
        if(n==0) return note;
        if(n==1) {
        note[1]=1;
        return note;
        }
        if(n>=2){
            note[1]=1;
        for(int i=2;i<n+1;i++){
            note[i]=note[i-2]+note[i-1];
        }}
        return note;
    }
    int fib(int n) {
        vector<int> no(n+1);
        memo(no,n);
        return no[n];
    }
};

题解3：（自底向上）

class Solution {
public:int fib(int n) {
        if(n==0) return 0;
        if(n==1) return 1;
        int prev=1;
        int pprev=0;
        int res;
        while(--n>0){
            res=pprev+prev;
            pprev=prev;
            prev=res;

        }
        return res;
    }
};

322. 零钱兑换

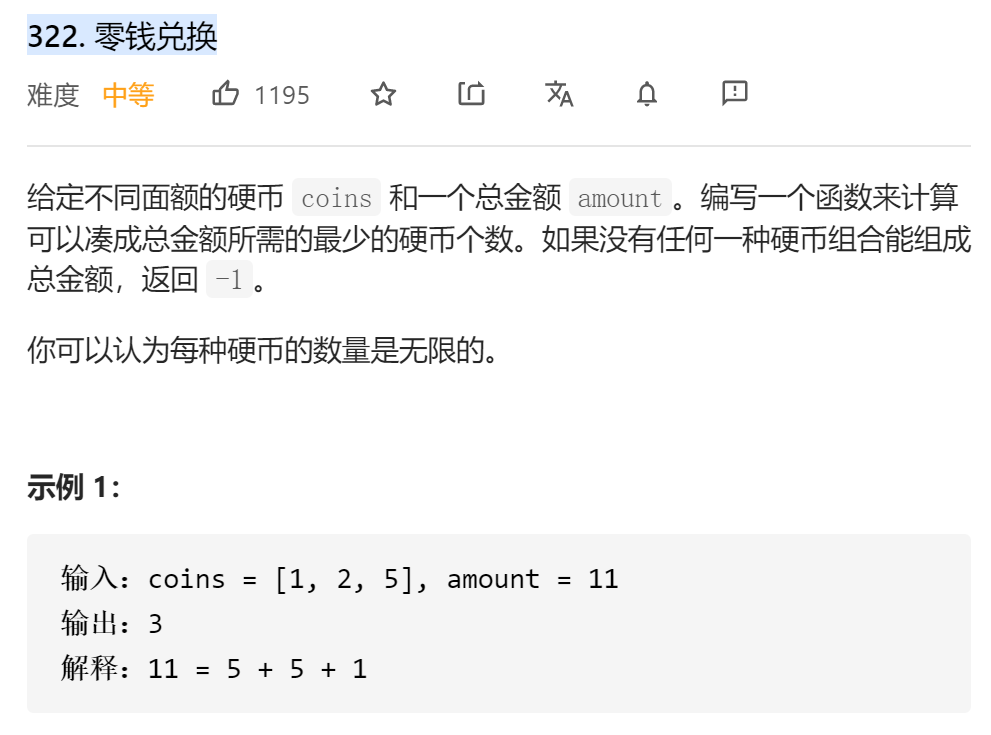
 题解1：（暴力递归，超出时间限制）

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        if(amount==0) return 0;
        if(amount<0) return -1;
        int res=100000;
        for (auto coin:coins){
            if(coinChange(coins, amount-coin)==-1) continue;
            res=min(res, 1+coinChange(coins, amount-coin));
        }
        return res==100000?-1:res;
    }
};

题解2：（备忘录）

class Solution {
    
public:
    int coinChange(vector<int>& coins, int amount) {
        if(amount==0) return 0;
        vector<int> memo(amount+1,-1);
        memo[0]=0;
        for(auto coin:coins){
            if(coin>amount) continue;
            memo[coin]=1;
        }
        for(int i=1;i<=amount;i++){
            if(memo[i]==1) continue;
            int minVal=100000;
            for(auto coin:coins){
                if(i-coin<0) continue;
                else{
                    minVal=min(minVal,1+memo[i-coin]);
                }
            }
             memo[i]=minVal;
        }
        return memo[amount]==100000?-1:memo[amount];
    }
};

70. 爬楼梯

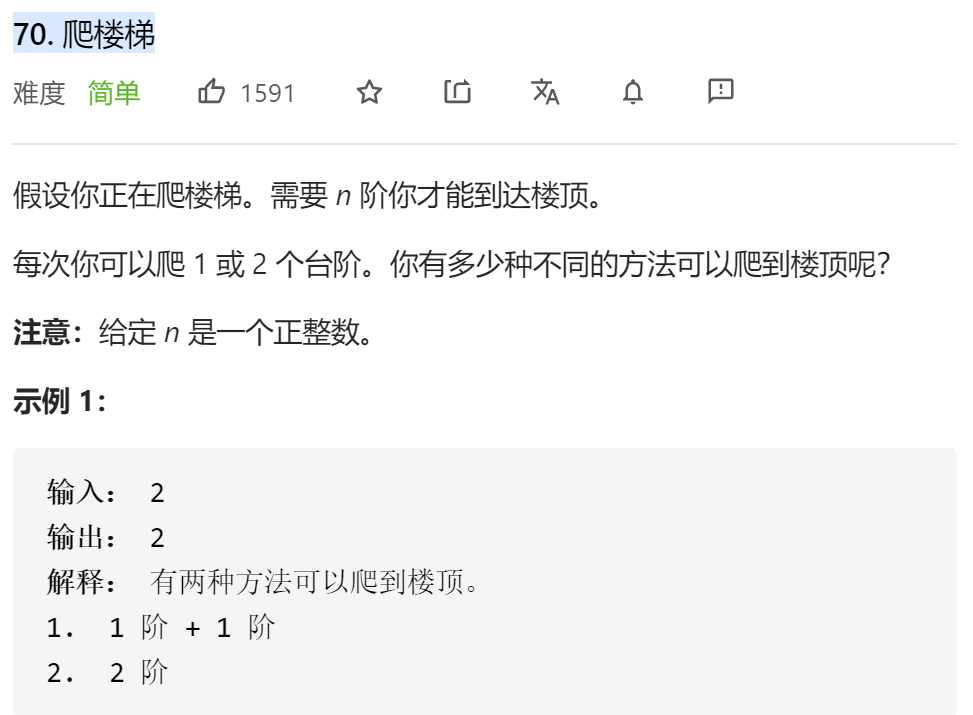
 题解1：（暴力递归，超出时间限制）

class Solution {
public:
    int climbStairs(int n) {
        if(n==1) return 1;
        if(n==2) return 2;
        return climbStairs(n-1)+climbStairs(n-2);
    }
};

题解2：（备忘录）

class Solution {
public:
    int climbStairs(int n) {
        vector<int> memo(n+1);
        if(n==1) return 1;
        if(n==2) return 2;
        memo[1]=1;
        memo[2]=2;
        for(int i=3;i<n+1;i++){
            memo[i]=memo[i-2]+memo[i-1];
        }
        return memo[n];
    }
};

题解3：（自底向上）

class Solution {
public:
    int climbStairs(int n) {
        
        if(n==1) return 1;
        if(n==2) return 2;
        int pprev=1;
        int prev=2;
        int res=0;
        for(int i=3;i<n+1;i++){
            res=pprev+prev;
            pprev=prev;
            prev=res;
        }
        return res;
    }
};

198. 打家劫舍

题解1：（暴力递归，超过时间限制）

class Solution {
public:
    int rob(vector<int>& nums) {
        return dp(nums, 0);
    }
    int dp(vector<int>& a, int start){
        if(start>=a.size()) return 0;
        int res=max(dp(a,start+1),dp(a, start+2)+a[start]);
        return res;
    }
};

题解2：（自底向上）

class Solution {
public:
    int rob(vector<int>& nums) {
        int pprev=0;
        int prev=0;
        int current=0;
        for(int i=nums.size()-1;i>=0;i--){
            current=max(pprev+nums[i],prev);
            pprev=prev;
            prev=current;
        }
        return current;
    }
};

213. 打家劫舍 II

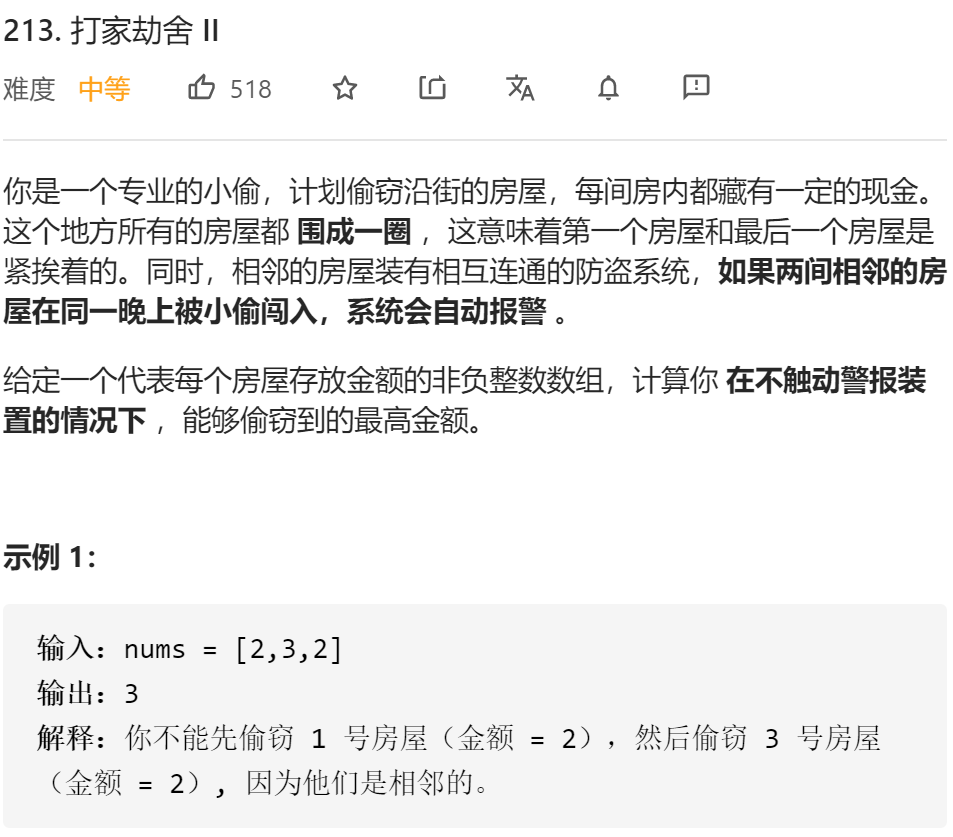
 题解1：（自底向上）

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size()==1) return nums[0];
        int pprev=0;
        int prev=0;
        int res,res2=0;
        for(int i=0;i<nums.size()-1;i++){
            res=max(nums[i]+pprev,prev);
            pprev=prev;
            prev=res;
        }
        pprev=0;
        prev=0;
        for(int i=nums.size()-1;i>=1;i--){
            res2=max(nums[i]+pprev,prev);
            pprev=prev;
            prev=res2;
        }
        return max(res,res2);
    }
};

746. 使用最小花费爬楼梯

 题解1：（暴力递归，超过时间限制）

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        cost.push_back(0);
        return dp(cost,cost.size()-1);
    }
    int dp(vector<int>& cost, int k){
        if(k==-1||k==-2) return 0;
        if(k==0) return cost[0];
        return min(dp(cost,k-1)+cost[k],dp(cost,k-2)+cost[k]);
    }
};

题解2：（自底向上）

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int pprev=0;
        int prev=0;
        int res=0;
        cost.push_back(0);
        for(int i=0;i<cost.size();i++){
            res=min(cost[i]+pprev,cost[i]+prev);
            pprev=prev;
            prev=res;
                    
        }
        return res;
    }
};

337. 打家劫舍 III

题解1：（暴力递归，超出时间限制）

class Solution {
public:
    int rob(TreeNode* root) {
        if(!root) return 0;
        int money=root->val;
        if(root->left){
            money+=rob(root->left->left)+rob(root->left->right);
        }
        if(root->right){
            money+=rob(root->right->left)+rob(root->right->right);
        }
        return max(money,rob(root->left)+rob(root->right));
    }
};

题解2：（哈希表备忘录）

class Solution {
    unordered_map<TreeNode*, int> note;
public:
    int rob(TreeNode* root) {
        if(!root) return 0;
        if(note.find(root)!=note.end()) return note[root];
        int money = root->val;
        if(root->left){
            money+=rob(root->left->left)+rob(root->left->right);
        }
        if(root->right){
            money+=rob(root->right->left)+rob(root->right->right);
        }
        int res=max(money, rob(root->left)+rob(root->right));
        note[root]=res;
        return res;
    }
};

题解3: （二维dp递归，优化空间复杂度）

class Solution {
public:
// 0 不抢； 1抢
    pair<int,int> dp(TreeNode* root){ //dp返回当前结点偷或不偷时能抢到的最大的钱
        if(!root) return {0,0};
        auto left  = dp(root->left);
        auto right = dp(root->right);
        
        return {root->val+left.second+right.second,max(left.first,left.second)+max(right.first,right.second)};
    }
    int rob(TreeNode* root) {
        
        return max(dp(root).first,dp(root).second);
    }
    
};