Spark机器学习(9)：FPGrowth算法

关联规则挖掘最典型的例子是购物篮分析，通过分析可以知道哪些商品经常被一起购买，从而可以改进商品货架的布局。

1. 基本概念

首先，介绍一些基本概念。

(1) 关联规则：用于表示数据内隐含的关联性，一般用X表示先决条件，Y表示关联结果。

(2) 支持度(Support)：所有项集中{X,Y}出现的可能性。

(3) 置信度(Confidence)：先决条件X发生的条件下，关联结果Y发生的概率。

2. Apriori算法

Apriori算法是常用的关联规则挖掘算法，基本思想是：

(1) 先搜索出1项集及其对应的支持度，删除低于支持度的项集，得到频繁1项集L1；

(2) 对L1中的项集进行连接，得到一个候选集，删除其中低于支持度的项集，得到频繁1项集L2；

...

迭代下去，一直到无法找到L(k+1)为止，对应的频繁k项集集合就是最后的结果。

Apriori算法的缺点是对于候选项集里面的每一项都要扫描一次数据，从而需要多次扫描数据，I/O操作多，效率低。为了提高效率，提出了一些基于Apriori的算法，比如FPGrowth算法。

3. FPGrowth算法

FPGrowth算法为了减少I/O操作，提高效率，引入了一些数据结构存储数据，主要包括项头表、FP-Tree和节点链表。

3.1 项头表

项头表(Header Table)即找出频繁1项集，删除低于支持度的项集，并按照出现的次数降序排序，这是第一次扫描数据。然后从数据中删除非频繁1项集，并按照项头表的顺序排序，这是第二次也是最后一次扫描数据。

下面的例子，支持度=0.4，阈值=0.4*10=4，因为D、F、G出现次数小于4次，小于阈值，所以被删除，项头表按照各一项集出现的次数重新排序。如ABCE=>EABC。

3.2 FP-Tree

3.2.1 FP-Tree的建立

FP-Tree(Frequent Pattern Tree)初始时只有一个根节点Null，将每一条数据里的每一项，按照排序后的顺序插入FP-Tree，节点的计数为1，如果有共用的祖先，则共用祖先的节点计数+1。

首先，插入第1条数据E：

插入第2条数据ABC：

插入第3条数据EABC：

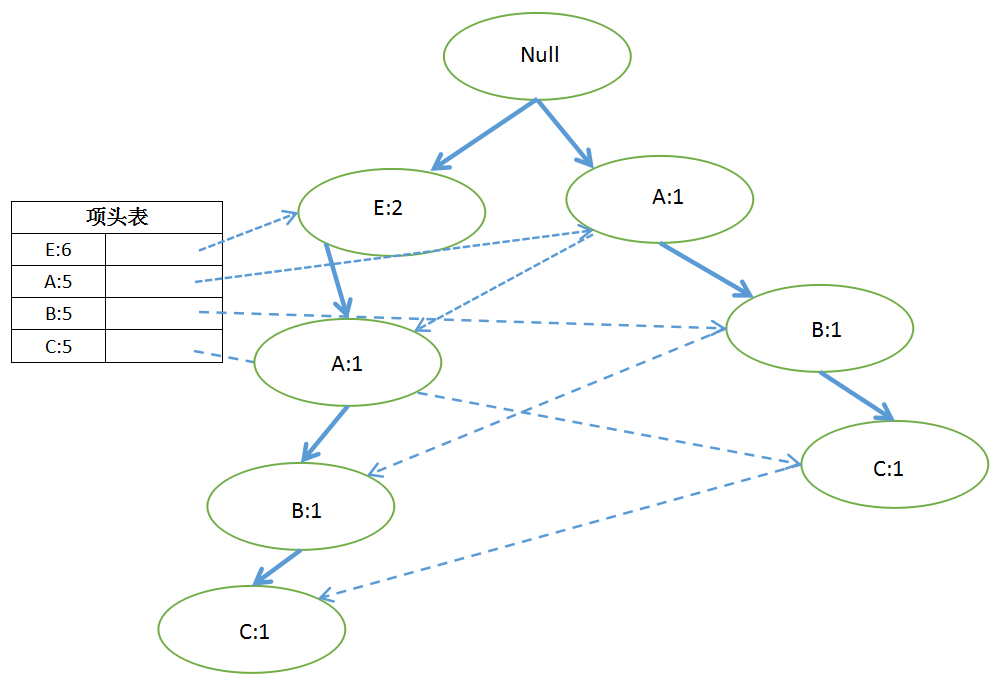
以此类推，所有数据都插入以后：

 

3.2.2 FP-Tree的挖掘过程

FP-Tree的挖掘过程如下，从长度为1的频繁模式开始挖掘。可以分为3个步骤：

(1) 构造它的条件模式基(CPB, Conditional Pattern Base)，条件模式基(CPB)就是我们要挖掘的Item的前缀路径；

(2) 然后构造它的条件FP-Tree(Conditional FP-tree)；

(3) 递归的在条件FP Tree上进行挖掘。

从项头表的最下面一项（也就是C）开始，包含C的3个CPB分别是EAB、E、AB，其计数分别为2、1、2，可以表示为CPB{<EAB:2>,<E:1>,<AB:2>}。累加每个CPB上的Item计数，低于阈值的删除，得到条件FP Tree(Conditional FP-tree)。如CPB{<EAB:2>,<E:1>,<AB:2>}，得到E:3，A:4，B:4，E的计数小于阈值4，所以删除，得到C的条件FP Tree如下：

在条件FP Tree上使用如下的算法进行挖掘：

procedure FP_growth(Tree, α){
if Tree 含单个路径P {
    for 路径 P 中结点的每个组合（记作β）{
        产生模式β ∪ α，其支持度support = β中结点的最小支持度；
    }
}
else {
    for each a i 在 Tree 的头部 {
        产生一个模式β = ai ∪ α，其支持度support = ai.support；
        构造β的条件模式基，然后构造β的条件FP Tree Treeβ；
        if Treeβ ≠ ∅ then
            调用FP_growth (Treeβ, β)；}
    }
}

 对于上面的条件FP Tree，可知是单个路径，可以得到以下的频繁模式：<AC:4>、<BC:4>、<ABC:4>。

4. MLlib的FPGrowth算法

直接上代码：

import org.apache.log4j.{ Level, Logger }
import org.apache.spark.{ SparkConf, SparkContext }
import org.apache.spark.rdd.RDD
import org.apache.spark.mllib.fpm.{ FPGrowth, FPGrowthModel }

/**
  * Created by Administrator on 2017/7/16.
  */
object FPGrowth {

  def main(args:Array[String]) ={
    // 设置运行环境
    val conf = new SparkConf().setAppName("FPGrowth")
      .setMaster("spark://master:7077").setJars(Seq("E:\Intellij\Projects\MachineLearning\MachineLearning.jar"))
    val sc = new SparkContext(conf)
    Logger.getRootLogger.setLevel(Level.WARN)

    // 读取样本数据并解析
    val dataRDD = sc.textFile("hdfs://master:9000/ml/data/sample_fpgrowth.txt")
    val exampleRDD = dataRDD.map(_.split(" ")).cache()

    // 建立FPGrowth模型,最小支持度为0.4
    val minSupport = 0.4
    val numPartition = 10
    val model = new FPGrowth().
      setMinSupport(minSupport).
      setNumPartitions(numPartition).
      run(exampleRDD)

    // 输出结果
    println(s"Number of frequent itemsets: ${model.freqItemsets.count()}")
    model.freqItemsets.collect().foreach { itemset =>
      println(itemset.items.mkString("[", ",", "]") + ":" + itemset.freq)
    }
  }

}

样本数据：

D E
A B C
A B C E
B E
C D E
A B C
A B C E
B E
F G
D F

运行结果：

参考文献：《数据挖掘概念与技术》。