1. 拉格朗日乘子(Lagrange Multiplier)法
假设函数z=f(x,y),求该函数的最小值,如果没有约束条件,则可以表示为minf(x,y),要求出minf(x,y)很简单,根据Fermat定理,分别对x和y求导数并让其等于0,如果是凸函数,则求出来的点就是函数取得最小值的点,该点的函数值即f(x,y)的最小值。
如果有等式约束条件g(x,y)=c,g(x,y)=c为(x,y)平面上的一条曲线,想象f(x,y)的等高线下降,当等高线和g(x,y)=c有交点时,满足约束条件,但肯定不是最优值,因为还可以继续下降。只有当下降到f(x,y)和g(x,y)=c相切时,这时两条曲线的切点处的f(x,y)的值才是最优值,如下图所示。
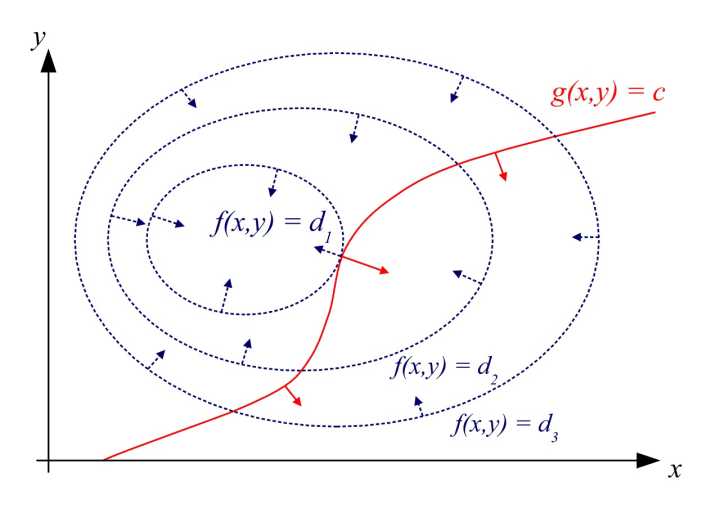
由上图可知,在切点处,两条曲线拥有共线的法向量,所以两条曲线的梯度(Gradient)成正比,即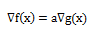 ,相当于把目标函数和约束条件写成一个函数,然后对该函数求导等于0,即可求得最优值。如果约束条件有多个,方法也是一样的。
,相当于把目标函数和约束条件写成一个函数,然后对该函数求导等于0,即可求得最优值。如果约束条件有多个,方法也是一样的。
所以,对于这类问题可以表示为:
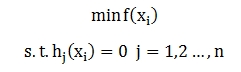
解决的方法是将目标函数和约束条件写成一个式子:
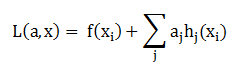
分别对xi求导数并让其等于0,可求得最优值。
2. KKT条件
以上是等式约束,如果是不等式约束的话,问题变成了:
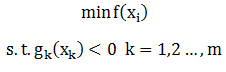
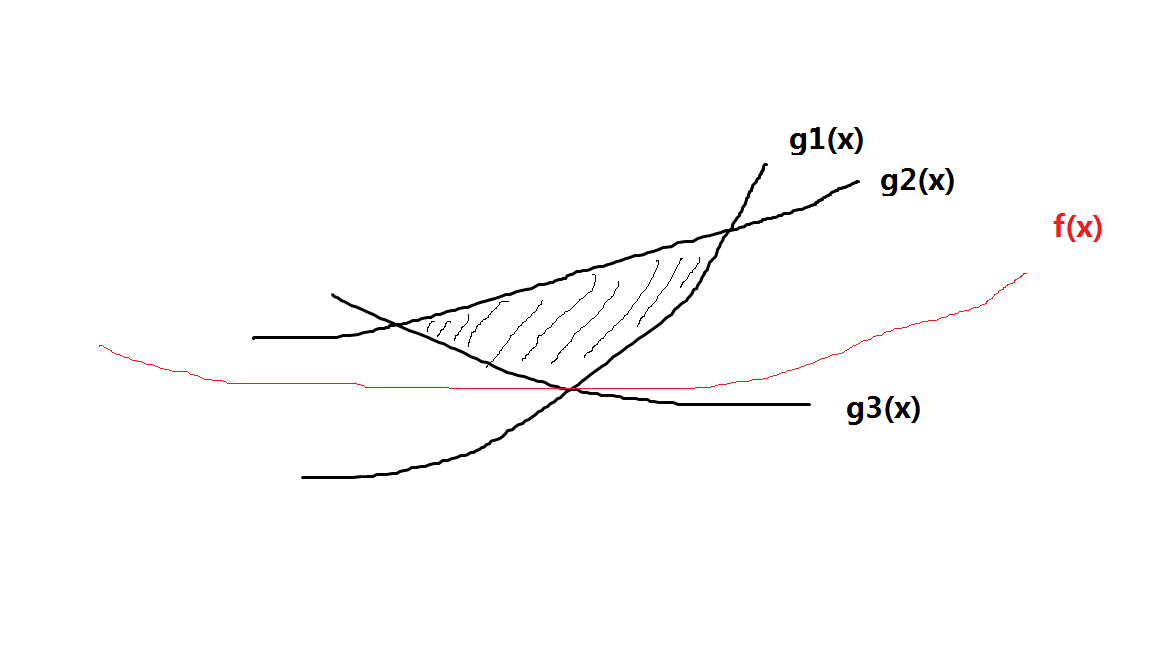
可以想象,多个约束条件构成了一个区域,这个区域就是自变量的范围。最优值肯定在这个区域的某一个顶点处取得,此时和这个顶点相关的约束条件等于0,和这个顶点不相关的约束条件(即不需要考虑的约束条件)不等于0。如下图所示,g1(x)、g2(x)、g3(x)围成了一个区域,最优值在g1(x)和g3(x)的交点处取得,此时g2(x)不需要考虑,则g1(x)和g3(x)的值为0,前面的系数可以不为0,g2(x)不为0,前面的系数必须为0。
因此,同样的可以把目标函数和约束条件写成一个式子:

对于 ,要么b=0,要么g(xi)=0,所以必须有
,要么b=0,要么g(xi)=0,所以必须有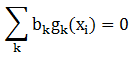 。
。
如果同时存在等式约束和不等式约束,则
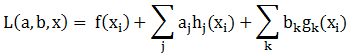
那么最优值必须满足以下3个条件:
(1) L对xi求导等于0;
(2)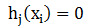 ;
;
(3)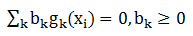 。
。
以上就是KKT条件。