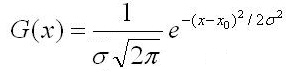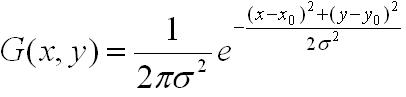高斯滤波是一种线性平滑滤波,适用于消除高斯噪声,在图像处理的降噪、平滑中应用较多,特别是对抑制或消除服从正态分布的噪声非常有效。
高斯滤波的过程其实就是对整幅图像进行加权平均操作的过程。滤波后图像上每一个像素的灰度值大小,由其本身和邻域内的其他像素共同决定。具体实现是:用一个大小为(2*N+1)的模板(或称卷积核、掩模)依次扫描图像中的每一个像素,用模板确定的邻域内像素的加权平均灰度替代模板中心像素点的灰度值。
一维、二维高斯分布
一维高斯函数表述为:
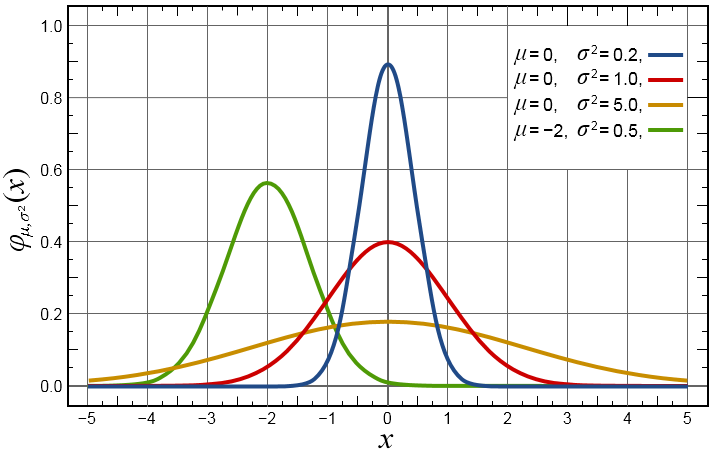
对应图形:
二维高斯函数表述为:
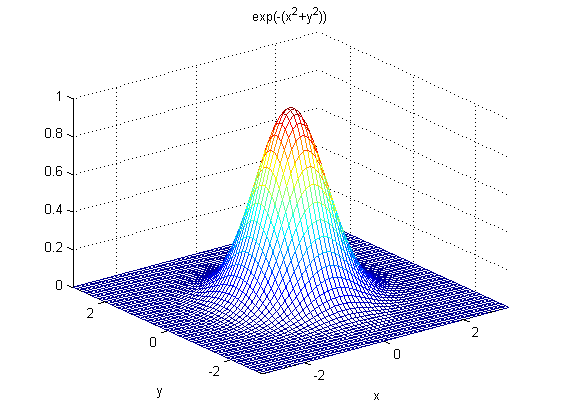
对应图形:
一些重要特性说明:
1. 一维二维高斯函数中μ是服从正态分布的随机变量的均值,称为期望或均值影响正态分布的位置,实际的图像处理应用中一般取μ=0;σ是标准差,σ^2是随机变量的方差,σ定义了正态分布数据的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中。
在图形或滤波效果上表现为:σ越大,曲线越扁平,高斯滤波器的频带就越宽,平滑程度就越好,σ越小,曲线越瘦高,高斯滤波的频带就越窄,平滑程度也越弱;
2. 二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的.一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑.旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向;
3. 高斯函数是单值函数。这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的。这一性质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真;
4. 相同条件下,高斯卷积核的尺寸越大,图像的平滑效果越好,表现为图像越模糊,同时图像细节丢失的越多;尺寸越小,平滑效果越弱,图像细节丢失越少;
以下对比一下不同大小标准差σ(Sigma)对图像平滑的影响:
原图:
卷积核尺寸5*5,σ=0.1:
卷积核尺寸5*5,σ=1:
对比可以看到,Sigma(σ)越大,平滑效果越明显。
C++对高斯卷积核参数求解:
#include "iostream"
#include "math.h"
using namespace std;
using namespace cv;
//******************高斯卷积核生成函数*************************
//第一个参数gaus是一个指向含有3个double类型数组的指针;
//第二个参数size是高斯卷积核的尺寸大小;
//第三个参数sigma是卷积核的标准差
//*************************************************************
void GetGaussianKernel(double **gaus, const int size,const double sigma);
int main(int argc,char *argv[])
{
int size=5; //定义卷积核大小
double **gaus=new double *[size];
for(int i=0;i<size;i++)
{
gaus[i]=new double[size]; //动态生成矩阵
}
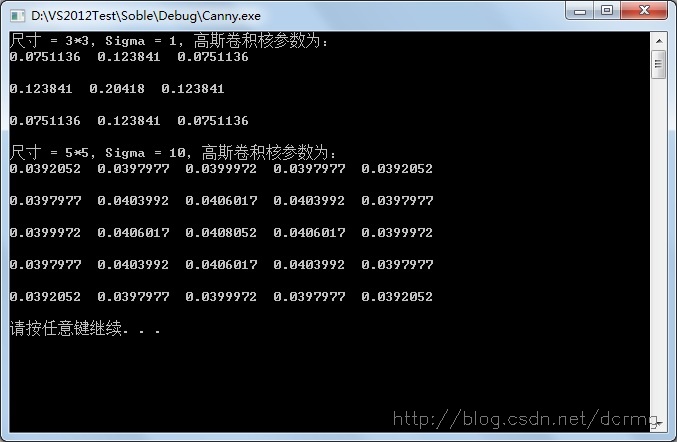
cout<<"尺寸 = 3*3,Sigma = 1,高斯卷积核参数为:"<<endl;
GetGaussianKernel(gaus,3,1); //生成3*3 大小高斯卷积核,Sigma=1;
cout<<"尺寸 = 5*5,Sigma = 10,高斯卷积核参数为:"<<endl;
GetGaussianKernel(gaus,5,10); //生成5*5 大小高斯卷积核,Sigma=1;
system("pause");
return 0;
}
//******************高斯卷积核生成函数*************************
void GetGaussianKernel(double **gaus, const int size,const double sigma)
{
const double PI=4.0*atan(1.0); //圆周率π赋值
int center=size/2;
double sum=0;
for(int i=0;i<size;i++)
{
for(int j=0;j<size;j++)
{
gaus[i][j]=(1/(2*PI*sigma*sigma))*exp(-((i-center)*(i-center)+(j-center)*(j-center))/(2*sigma*sigma));
sum+=gaus[i][j];
}
}
for(int i=0;i<size;i++)
{
for(int j=0;j<size;j++)
{
gaus[i][j]/=sum;
cout<<gaus[i][j]<<" ";
}
cout<<endl<<endl;
}
return ;
}求得的高斯卷积核参数存放在一个大小为N*N的数组内: