范畴(category)不仅仅是一种数学语言,更是一种哲学观点。代数思想的精髓在于:抽象,但是简洁。概括性极高。
0. 预备概念
- 态射:morphism,最常见的这种过程的例子是在某种意义上保持结构的函数或映射。在集合论中,例如,态射就是函数,在群论中,它们是群同态,而在拓扑学中,它们是连续函数。在泛代数(universal algebra)的范围,态射通常就是同态。
- 对态射和它们定义于其间的结构(或对象)的抽象研究构成了范畴论的一部分。在范畴论中,态射不必是函数,而通常被视为两个对象(不必是集合 )间的箭头。不象映射一个集合的元素到另外一个集合,它们只是表示域(domain)和陪域(codomain)间的某种关系。
- 尽管态射的本质是抽象的,多数人关于它们的直观(事实上包括大部分术语)来自于具体范畴的例子,在那里对象就是有附加结构的集合而态射就是保持这种结构的函数。
2. 基本思想
代数思想不同于分析思想,它的初衷是希望用最简洁的语言把尽可能多的概念统一起来,亦即对普适性的追求。(也即代数思想是自下而上的归纳,分析是自上而下的细化)。
大部分数学对象抽象到不能抽象的地步,就必须用范畴的语言去描述。简而言之,范畴是大部分数学对象的极限抽象(终极抽象)。这里的“抽象”,是指把不同概念用同一种方式描述起来的过程。例如,所有的集合组成一个范畴,所有的线性空间组成一个范畴,所有的群组成一个范畴,所有的流形也组成一个范畴,因此范畴是集合、线性空间、群、流形的抽象。
范畴是对共性的描述。
但抽象不能盲目,因为作为一个数学对象(object),必须要有其内在的运算规则(规则定义了对象)才行,否则范畴这个概念也太宽泛了。为了赋予范畴内在的运算规则,需要“态射(morphism,或者箭头)”这个概念。而且态射不能乱射,必须要射得有规律,这种规律称为结合律。我们小学就知道,加法和乘法都有结合律。有了内在的运算规则(相同范畴),需不需要外在的运算规则(不同范畴之间)呢?所谓外在的运算规则,是指对于两个不同范畴,有没有某种方式把它们联系起来。这就是“函子(functor)”概念的由来。外在运算当然也不能随便定义,必须保持范畴的内在运算结构(也就是箭头方向)不变。
无论范畴也好,内在外在运算也好,所有东西都太抽象,必须想个方法把它们可视化。代数学家的可视化工具叫做交换图(commutative diagram)。如下是一个简单的交换图:
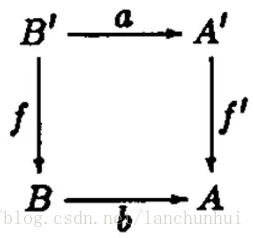
其中两个A是范畴1(换个名字也行)的两个对象,两个B是范畴2的两个对象,两个f分别是两个范畴的“内在运算”(态射),a和b是范畴2到范畴1的“外在运算”(函子)。这张交换图是说, 也就是说函子不仅要保持对象的不变性,还要保持态射的不变性。态射最简单的例子就是加法。
2. 范畴的数学定义
我们甚至可以进一步把这些概念具体化,例如每当我们提到范畴时,可以参照两个实例:群范畴或线性空间范畴 :
- 同态:
- 态射就是群之间的同态
- 线性空间之间的线性变换,
- 函数子:
- 群范畴和线性空间范畴之间的函子就是群表示。
上一节中函子和态射之间的交换图告诉我们,群表示其实就是把群转换为相性代数的过程。从这里大家可以体会到范畴论在数学中的威力—-把很多数学概念用最简洁语言表示出来。