根据其提出者,John Joseph Hopfield 命名。Hopfield 在 1982 年提出的划时代的:Neural networks and physical systems with emergent collective computational abilities 一文。顾名思义,从论文的名字中我们就可看出,Hopfield 神经网络是将物理学的相关思想(动力学)引入到神经网络的构造当中,事实上,Hopfield 本人正是一位物理学家。
这里所谓动力学的方式,不像 BP 神经网络那样给定输入和输出,通过权值的计算更新以及激活函数的转移,最后能够最小化和输出之间的误差,而动力学的方式则是给模型一定的输入之后,系统就会陷入一个动力学过程里面,反复震荡和计算,最后达到一个稳态。最后能够达到像人一样的具备联想能力的网络。
0. 基本认识
- 每一个神经元和其他神经元都是连接的,因此和 BP 神经网络的不同也在于,Hopfield 神经网络其实没有分层的概念;
1. DHNN
- DHNN,Discrete Hopfield Neural Networks,存在离散型 HNN,自然也少不了 CHNN,Continuous HNN,连续型网络。
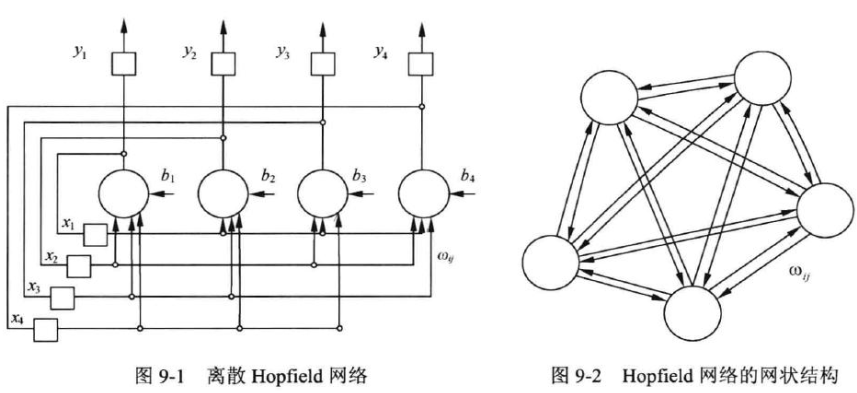
- 从其对应的网状结构可以清晰地看出,DHNN 和其他神经网络不同的是,DHNN 并没有层(Layer)的概念,也没有前向和后向的区别。
bi ,称为每一个神经元(neuron)的门槛值,因为最终是要用加权值和减去该值,又可称其为截断值,netj=∑i=1nwijxi−Tj,j=1,2,…,n 对于输出而言还存在一个反馈回路,第一个神经元的输出会反馈给其他所有神经元,反馈回自己的权值为 0,其他神经元得到的反馈值会作为下一轮的输入值;
wii=0 ,此外还存在一个对称性的规定,wij=wji
2. 两个定理(稳态性的证明)
吸引子(attractor):
定理之一:对于 DHNN 网,若按异步方式调整网络状态,且连接矩阵
W 为对称阵,则对于任意初态,网络都最终收敛到一个吸引子;此时我们引入能量函数(energy function)的定义,
E(t)=−12XT(t)WX(t)+XT(t)T 令能量函数的改变量为
ΔE ,网络状态的改变量为ΔX ,则有:ΔE(t)=E(t+1)−E(t)ΔX(t)=X(t+1)−X(t) 将相关变量的定义代入进
ΔE(t) ,可得:ΔE(t)=−12[X(t)+ΔX(t)]TW[X(t)+ΔX(t)]+(X(t)+ΔX(t))TT−E(t)=−ΔXT[WX−T]−12ΔXTWΔX 由于该定理是规定按照异步工作方式,第
t 个时刻只有一个神经元调整状态,