1、Log-Structured 结构
在计算机存储数据结构的发展中,Log-Structured 结构的诞生为许多文件系统或者是数据库打下了坚实的基础。
比如说,Google 的三驾马车之一,Bigtable 文件系统的底层存储数据结构采用的就是 Log-Structured 结构,还有大家所熟知的 MongoDB 和 HBase 这类的 NoSQL 数据库,它们的底层存储数据结构其实也是 Log-Structured 结构。
而 Log-Structured 结构和平衡树有着莫大的关系,因为在这些框架应用里面,通常都会使用平衡树来优化数据的查找速度。
在这一讲中,我会先介绍什么是 Log-Structured 结构,而在下一讲中,再详细介绍平衡树数据结构是如何被应用在 Log-Structured 结构中的。
我们先来看看一个常见的问题应用。假设一个视频网站需要一个统计视频观看次数的功能,如果给你来设计的话,会采用哪种数据结构呢?
你可能会觉得这并不难,我们可以运用哈希表这个数据结构,以视频的 URL 作为键、观看次数作为值,保存在哈希表里面。所有保存在哈希表里面的初始值都为 0,表示并无任何人观看,而每次有人观看了一个视频之后,就将这个视频所对应的值取出然后加 1。
刚开始的时候,这个设计思路可能运行得很好。可当用户量增大了之后,会发现在更新哈希表的时候必须要加锁,不然的话,大量的这种并行 +1 操作可能会覆盖掉各自的值。
比方说,在同一时间,有两个用户都观看了一个视频,它们都根据视频的 URL 在哈希表中取出了观看次数的值 0,在更新操作 +1 了之后,都把 1 这个值保存在了哈希表中,而实际上,哈希表中的值应该是 2。
不难发现,这种操作的瓶颈其实是在更新操作,也就是写操作上。
那有没有方法可以不用顾及写操作的高并发问题,同时也可以最终获得一个准确的结果呢?答案就是使用 Log-Structured 结构。
Log-Structured 结构,有时候也会被称作是 Append-only Sequence of Data,因为所有的写操作都会不停地添加进这个数据结构中,而不会更新原来已有的值,这也是 Log-Structured 结构的一大特性。
看看在采用了 Log-Structured 结构之后,在上面的统计视频网站观看次数的应用中,底层的数据结构变成怎么样了。
假设现在网站总共有三个视频,URL 分别就是 A、B 和 C,那一个可能的数据结构图就如下图所示:

从上图中可以看到,这样的数据结构其实和数组非常像,数组里的值就保存着 URL 和 1,每次有新用户观看过视频之后,就会将 URL 和 1 加到数组的结尾。在上面的例子中,我们只需要遍历一遍这个数组,然后将不同的 URL 值加起来就可以得到观看的总数,例如 A 的观看总数为 8 次,B 为 3 次,C 为 5 次。
这其实就是 Log-Structured 结构的本质了,这样一个最基本的 Log-Structured 结构,其实在应用里会有很多的问题。比如说:
- 一个数组不可能在内存中无限地增长下去,我们要如何处理呢?
- 如果每次想要知道结果,就必须遍历一遍这样的数组,时间复杂度会非常高,那该怎么优化呢?
- 平衡树是如何被应用在里面的呢?
2、LSM 树在 Apache HBase 等存储系统中的应用
Log-Structured 结构的优化
首先,可以定义一个大小为 N 的固定数组,我们称它为 Segment,一个 Segment 最多可以存储 N 个数据,
当有第 N+1 个数据需要写入 Log-Structured 结构的时候,我们会创建一个新的 Segment,然后将 N+1 个数据写入到新的 Segment 中。
以下图为示,我们定义一个 Segment 的大小为 16,当 Segment 1 写满了 16 个数据之后,会将新的数据写入到 Segment 2 里。

说到这里,我们的 Log-Structured 结构还是一直在往内存里添加数据,并没有解决最终会消耗完内存的问题。
这时候就到 Compaction 大显身手的时候了,在当 Segment 到达一定数量的时候,Compaction 会通过后台的线程,把不同的 Segments 合并在一起。
假设我们定义当 Segment 的数量到达两个的时候,后台线程就会执行 Compaction 来合并结果。如图:
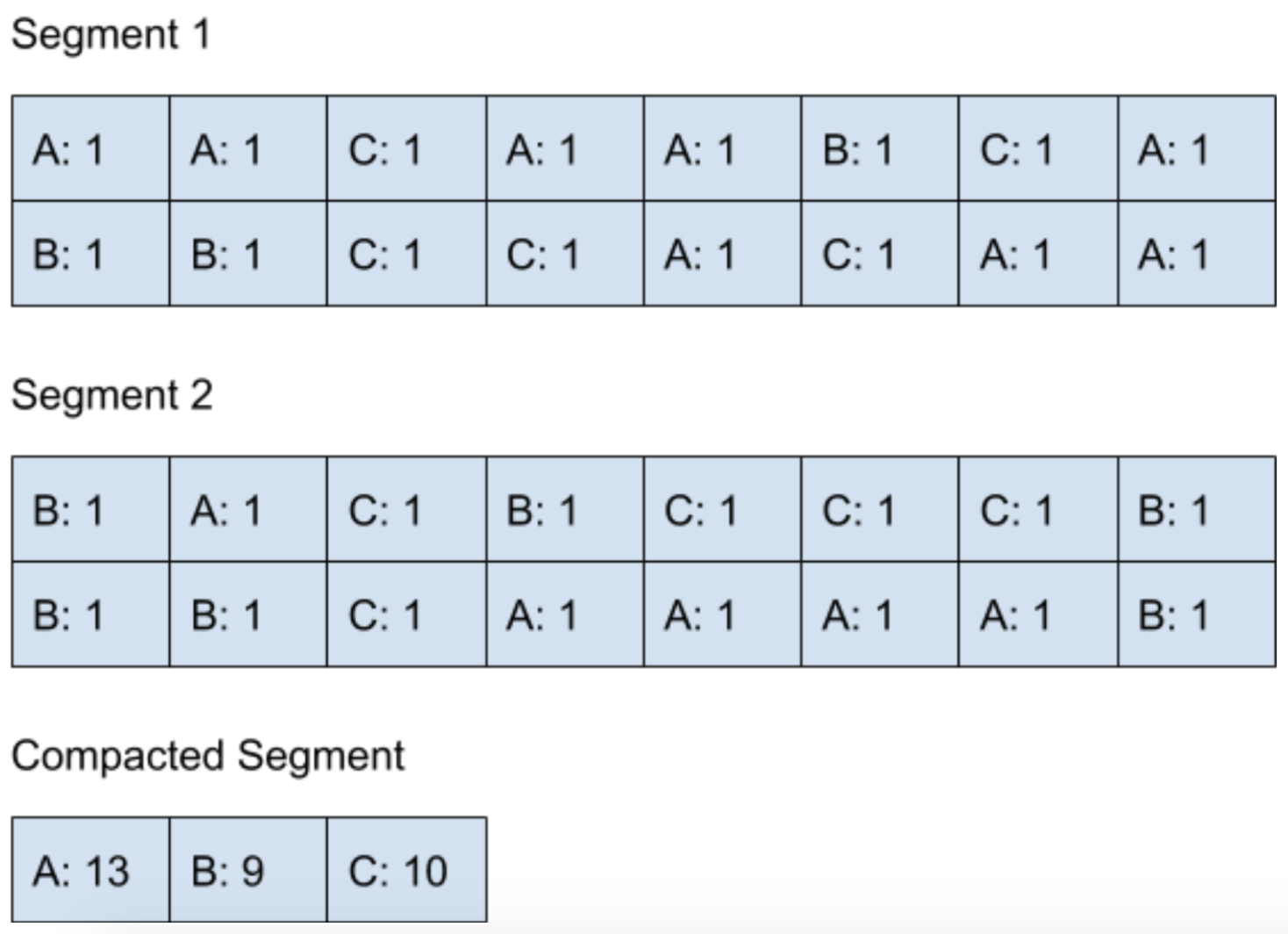
在 Compaction 完成了之后,对于结果的读取就可以从 Compacted Segment 里面读取了。因为这时候所有的结果已经存放在 Compacted Segment 里面了,所以就可以删除 Segment 1 和 Segment 2 来腾出内存空间了。
整个 Compaction 的过程会不断地递归进行下去,当 Compacted Segment 满了以后,后台线程又可以对 Compacted Segment 进行 Compaction 操作,再次合并所有结果。
你会发现,当采用了这种优化之后,写操作还是可以十分高效地进行下去,同时也不会占用大量的内存空间。
3、SSTable 和 LSM 树
上面所讲到的 Log-Structured 结构的这种 Compaction 优化,其实是 LSM 树的一个基础,在学习 LSM 树之前,我们先来了解一个新的数据结构,即 SSTable。
SSTable(Sorted String Table)数据结构是在 Log-Structured 结构的基础上,多加了一条规则,就是所有保存在 Log-Structured 结构里的数据都是键值对,并且键必须是字符串,在经过了 Compaction 操作之后,所有的 Compacted Segment 里保存的键值对都必须按照字符排序。
我们假设现在想利用 Log-Structured 结构来保存一本书里的词频,为了方便说明,把 Segment 的大小设为 4。在刚开始的时候,这个 Log-Structured 结构在经过了 Compaction 操作之后,内存图会变成如下图所示:
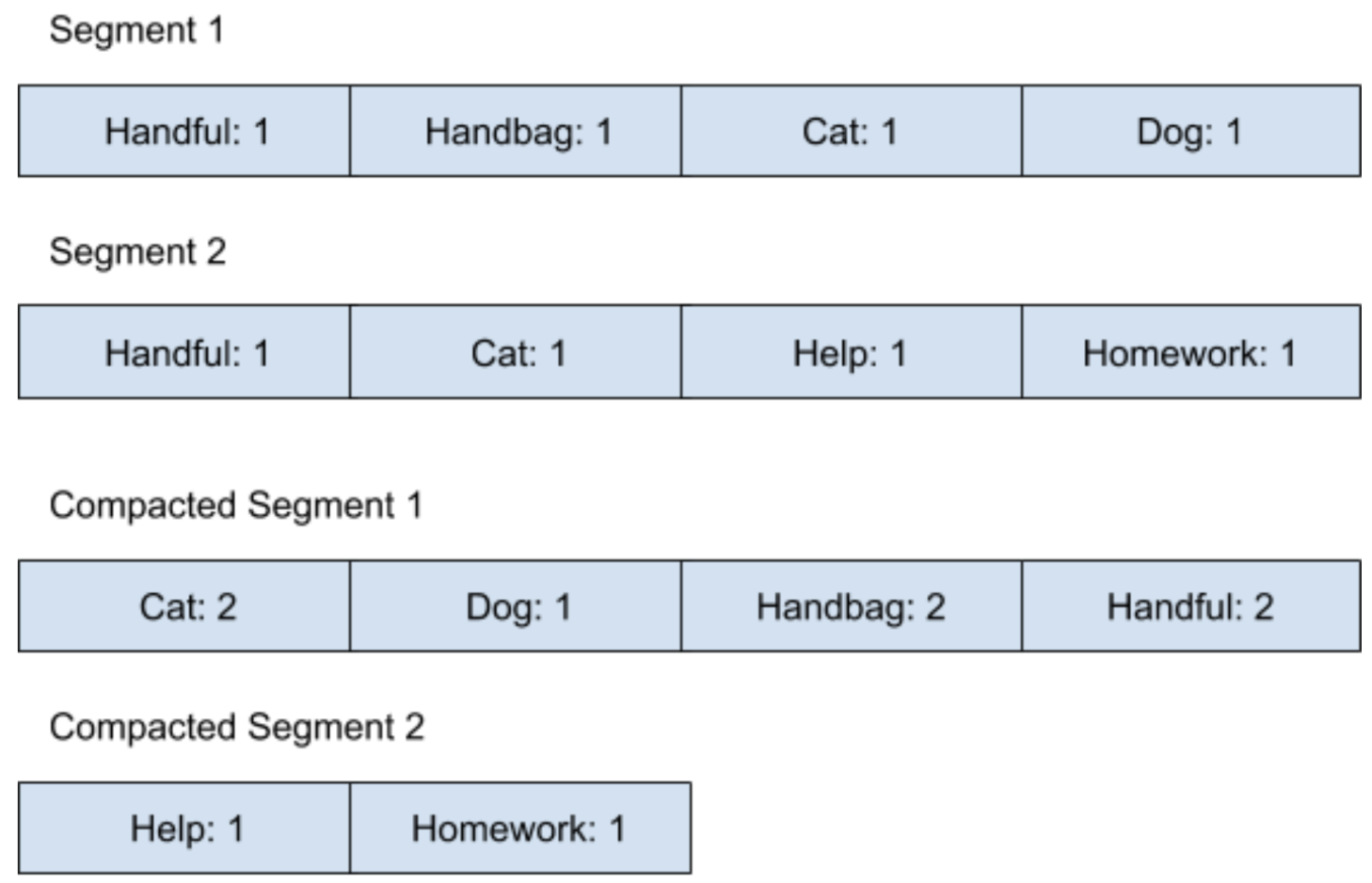
可以看到,所有的 Compacted Segment 都是按照字符串排序的。当我们要查找一个单词出现的次数时,可以去遍历所有的 Compacted Segment,来看看这个单词的词频,当然了,因为所有数据都是按照字符串排好序的,如果当遍历到的字符串已经大于我们要找的字符串时,就表示并没有出现过这个单词。
这时候你可能会有一个疑问,Log-Structured 结构是指不停地将新数据加入到 Segment 的结尾,像这种 Compaction 的时候将字符串排序应该怎么做呢?此时我们就需要上一讲中所讲到的平衡树了。
我们先来复习一下二叉查找树里的一个特性:二叉查找树的任意一个节点都比它的左子树所有节点大,同时比右子树所有节点小,说到这里你是不是有点恍然大悟了。
如果我们将所有 Log-Structured 结构里的数据都保存在一个二叉查找树里,当写入数据时其实是按照任意顺序写入的,而当读取数据时是按照二叉查找树的中序遍历来访问数据的,其实就相当于按字符串顺序读取了。
在业界上,我们为了维护数据结构读取的高效,一般都会维护一个平衡树,比如,在上一讲中说到的红黑树或者 AVL 树。
而这样一个平衡树在 Log-Structured 结构里通常被称为 memtable。
而上面所讲到的概念,通过内部维护平衡树来进行 Log-Structured 结构的 Compaction 优化,这样一种数据结构被称为是 LSM 树(Log-Structured Merge-Tree),它是由 Patrick O'Neil 等人在 1996 年所提出的。
LSM 树的应用
在数据库里面,有一项功能叫做 Range Query,用于查询在一个下界和上界之间的数据,比如,查找时间戳在 A 到 B 之内的所有数据。许多著名的数据库系统,像是 HBase、SQLite 和 MongoDB,它们的底层索引因为采用了 LSM 树,所以可以很快地定位到一个范围。
比如,如果内存里保存有以下的 Compacted Segments:

如果我们的查询是需要找出所有从 Home 到 No 的数据,那我们就知道,可以从 Compacted Segment 2 到 Compacted Segment 3 里面去寻找这些数据了。
同样的,采用 Lucene 作为后台索引引擎的开源搜索框架,像 ElasticSearch 和 Solr,底层其实运用了 LSM 树。
因为搜索引擎的特殊性,有可能会遇到一些情况,那就是:所搜索的词并不在保存的数据里,而想要知道一个数据是否存在 Segment 里面,必须遍历一次整个 Segment,时间开销还并不是最优化的,所以这两个搜索引擎除了采用 LSM 树之外,还会利用 Bloom Filter 这个数据结构,它可以用来判断一个词是否一定不在保存的数据里面。