1、图的实现方式
两种图的实现方式:
- 一种是邻接矩阵法。
- 另一种是邻接链表法。
这两种实现方式将会影响到我们后面算法的应用。
邻接矩阵法
使用邻接矩阵法的基本思想是开一个超大的数组,用数组中间元素的 true/false 来表达边,有 V 个节点的图,需要一个 V × V 大小的数组。
下面这个例子中有 V0 ~ V4 总共 5 个节点,可以看到我们已经画出了一个 5 × 5 的二维数组 G。
如果有从 Vi 指向 Vj 的边,那么 G[i][j] = true,反之如果没有边,则 G[i][j] = false。
有 V4 指向 V2 的边,那么 G[4][2] = true。V0 和 V2 之间的边是无向的,也就是说我们需要 G[0][2] = true 同时 G[2][0] = true。
再看到 V3 有指向自己的边,所以 G[3][3] 也是 true。

邻接链表法
邻接链表法的核心思想是把每一个节点所指向的点给存储起来。
比如还是上面的例子,如果我们用邻接链表法表达的话,则需要一个含 5 个元素的数组,用来存储这样的 5 个节点,然后每个节点所指向的点都会维护在一个链表中。
比如,V0 指向了 V1、V4、V2 三个节点,那在内存中就会有从 0 指向 1 接着指向 2、指向 4 这样的一个链表。同理我们看到 V4 指向了 V0 和 V2,在内存中就要维护一个 4→0→2 的单向链表。
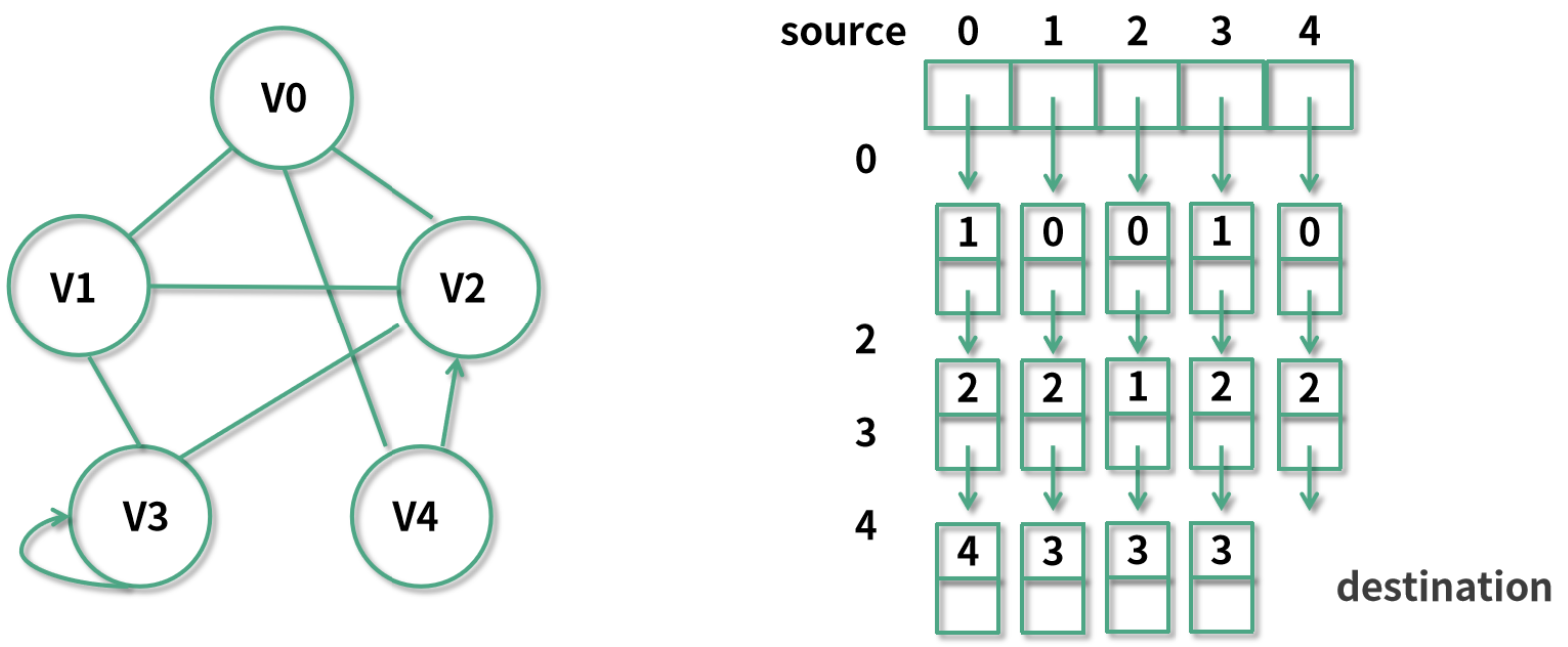
邻接链表法的核心思想是:把每一个节点所指向的点给存储起来。
比如还是上面的例子,如果我们用邻接链表法表达的话,则需要一个含 5 个元素的数组,用来存储这样的 5 个节点,然后每个节点所指向的点都会维护在一个链表中。
比如,V0 指向了 V1、V4、V2 三个节点,那在内存中就会有从 0 指向 1 接着指向 2、指向 4 这样的一个链表。同理我们看到 V4 指向了 V0 和 V2,在内存中就要维护一个 4→0→2 的单向链表。
2、图的拓扑排序
什么是拓扑排序呢?拓扑排序指的是对于一个有向无环图来说,排序所有的节点,使得对于从节点 u 到节点 v 的每个有向边 uv,u 在排序中都在 v 之前。拿我们之前讲过的西红柿炒鸡蛋这个例子来说吧。

一个合法的拓扑排序,必须使得被依赖的任务首先完成。在我们西红柿炒鸡蛋这个菜的加工过程中,要保证打鸡蛋在炒鸡蛋之前,买番茄在洗番茄之前,因为炒鸡蛋依赖于打鸡蛋,在我们的图中有打鸡蛋指向炒鸡蛋的边。
所以说一个合理的拓扑排序是能够保证有依赖关系的任务能够被合理完成。不如你思考一下为什么拓扑排序只适用于有向无环图呢?
我们来看一个经典的例子,那就是“鸡生蛋、蛋生鸡”。
先有鸡还是先有蛋 (Chicken Egg Dilemma)就是一个无法被拓扑排序的有环图,因为鸡依赖于蛋,蛋又依赖于鸡,你无法把鸡排在蛋前面,也不能把蛋排在鸡的前面。
拓扑排序的实现方式
首先我们来看看两个简单的概念,图的入度和出度。
- 一个有向图的入度:指的是终止于一个节点的边的数量;
- 有向图的出度:指的是始于一个节点的边的数量。以下图为例:
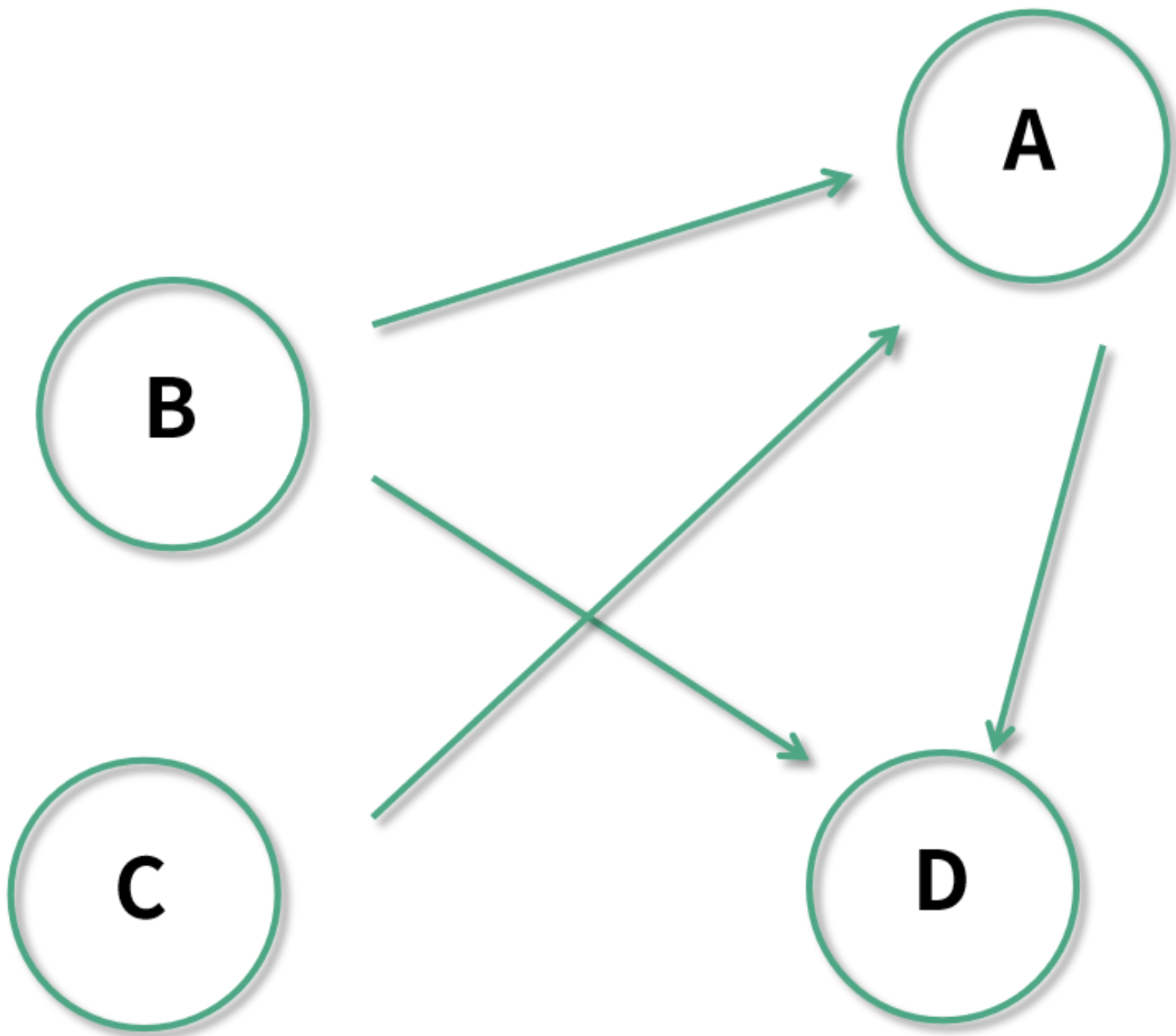
节点 A 的入度为 2,节点 B 的入度则为 0;而节点 B 的出度为 2,节点 D 的出度则为 0。
卡恩算法是卡恩于 1962 年提出的算法,它其实是贪婪算法的一种形式。简单来说就是,假设 L 是存放结果的列表,我们先找到那些入度为零的节点,把这些节点放到 L 中,因为这些节点没有任何的父节点;然后把与这些节点相连的边从图中去掉,再寻找图中入度为零的节点。对于新找到的这些入度为零的节点来说,他们的父节点都已经在 L 中了,所以也可以放入 L。
重复上述操作,直到找不到入度为零的节点。如果此时 L 中的元素个数和节点总数相同,则说明排序完成;
如果 L 中的元素个数和节点总数不同,则说明原图中存在环,无法进行拓扑排序。下面我们来看看这个算法的伪代码:
L ← Empty list that will contain the sorted elements S ← Set of all nodes with no incoming edge while S is non-empty do remove a node n from S add n to tail of L for each node m with an edge e from n to m do remove edge e from the graph if m has no other incoming edges then insert m into S if graph has edges then return error (graph has at least one cycle) else return L (a topologically sorted order
怎么样?学到这里你就掌握了 Spark 运算引擎的核心,即拓扑排序。
一旦 Spark 确立好了大数据处理的有向无环图,它就会对数据处理步骤进行拓扑排序,找到合理的处理顺序。
3、图的最短路径
图的最短路径也是非常常见的图的应用,最短路径顾名思义就是在一个有权重的图中,找到两个点之间权重之和最短的路径。
举例来说下,图中所有节点都是不同的城市,每一条边都是连接城市之间的道路距离。
比如 1 号节点是武汉,那么我们想要快速地把医疗物资送到武汉的话,就需要找到通向武汉最短的路线。
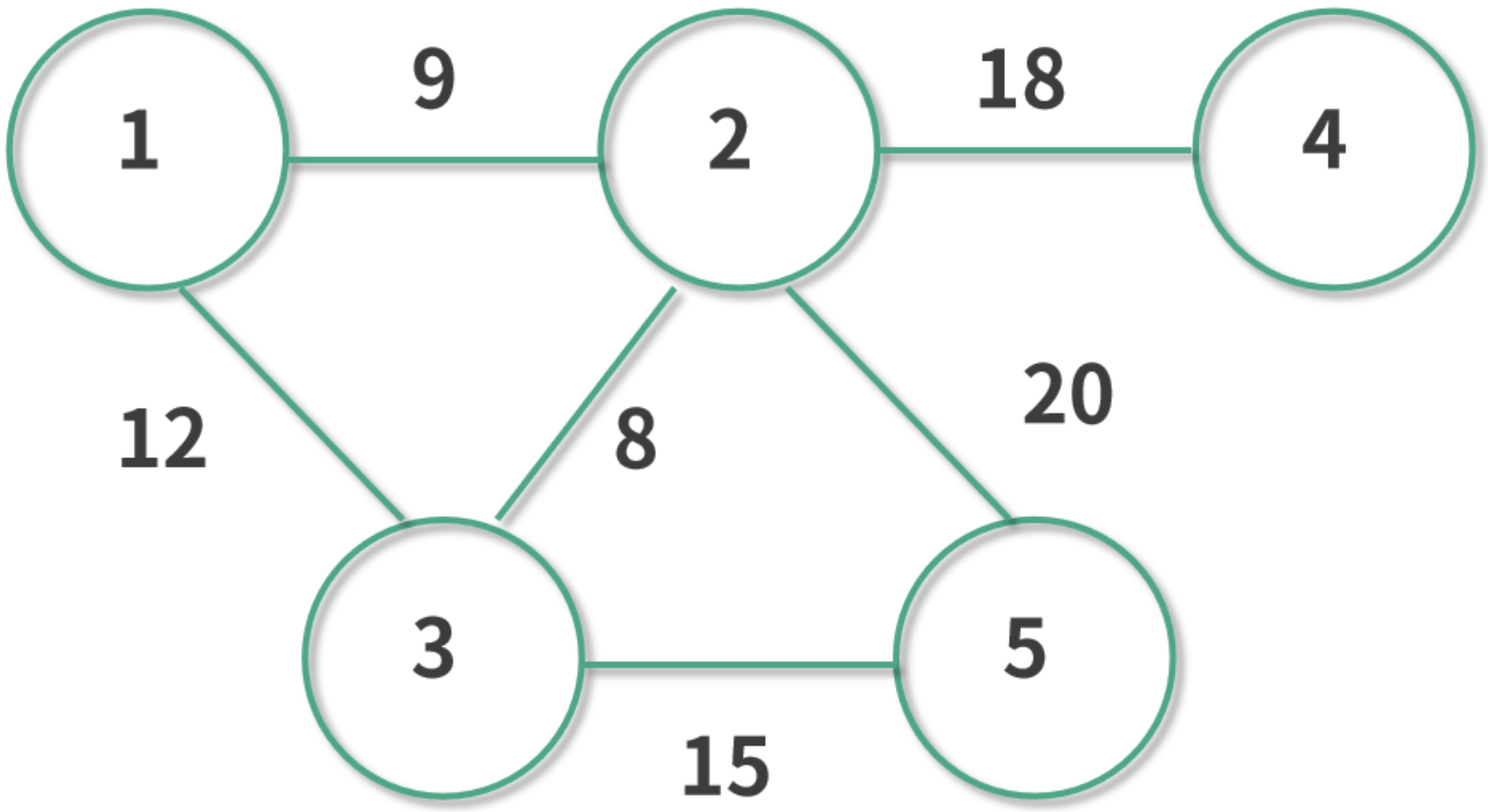
假如我们有一大批口罩在 5 号城市,想要送往武汉的话可以选择走 5-2-1 这条路线,或者 5-3-1 这条路线,甚至 5-2-3-1 等很多路线。
在这个例子中我们很容易发现,5-2-1 这条路线的总距离是 20 + 9 = 29,5-3-1 这条路线的总距离是 12+15 = 27,可见我们应该选择 5-3-1 这个路线。
Dijkstra 算法
我们怎样让计算机找到最短路径呢?这便是大名鼎鼎的 Dijkstra 算法。
最经典的 Dijkstra 算法原始版本仅适用于找到两个固定节点之间的最短路径,后来更常见的变体固定了一个节点作为源节点,然后找到该节点到图中所有其他节点的最短路径,从而产生一个最短路径树。我们这一讲会重点讲解最经典的也就是真正业界应用最多的场景,即两个节点都固定。
这个算法是通过为每个节点 v 保留当前为止所找到的从 s 到 v 的最短路径来工作的。
在初始时,原点 s 的路径权重被赋为 0(即原点的实际最短路径 = 0),同时把所有其他节点的路径长度设为无穷大,即表示我们不知道任何通向这些节点的路径。
当算法结束时,d[v] 中存储的便是从 s 到 v 的最短路径,或者如果路径不存在的话,则是无穷大。
伪代码如下所示:
function Dijkstra(Graph, source): create vertex set Q for each vertex v in Graph: dist[v] ← INFINITY prev[v] ← UNDEFINED add v to Q dist[source] ← 0 while Q is not empty: u ← vertex in Q with min dist[u] remove u from Q for each neighbor v of u: // only v that are still in Q alt ← dist[u] + length(u, v) if alt < dist[v]: dist[v] ← alt prev[v] ← u return dist[], prev
4、总结
这一课时我们学习了两种图在应用中最重要的算法,先是图的拓扑排序,揭开了 Spark 最核心的机密算法,之后是图的最短路径算法,将会在下一讲中应用到。