支持向量机需要解决的问题:找出一条最好的决策边界将两种类型的点进行分开

这个时候我们需要考虑一个问题,在找到一条直线将两种点分开时,是否具有其他的约束条件,这里我们在满足找到一条决策边界时,同时使得距离边界最近的点到边界的距离最远,对于下图而言,我们可以看出右边的图比左边的图的分类效果要好,因为点到边界的距离较大,这样得到的决策边界具有较好的泛化能力。

SVR的求解过程
首先我们需要写出点到直线或者平面的距离,这里以平面为例
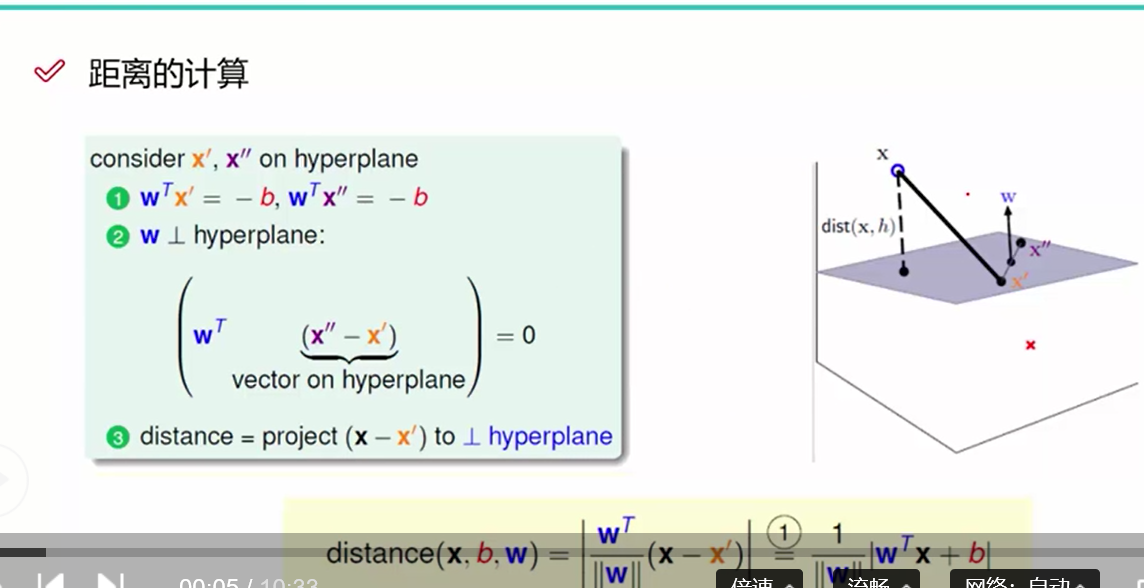
我们需要求得的是dist(x, h)即x点到平面的距离,我们x首先在平面上找到一个点x‘, a*b = |a|*|b|*cos(theta)
w^T*(x-x') / |w| = (x-x') * cos(theta) ----1 表示的是dist(x, h)
w表示的是法向量,因为x'为一个随机点,假设在平面上存在一个x',使得w^T*x' + b = 0 ---2
将上述的2式带入到1式中,对1式进行化解
dist(x, h) = 1/|w| * |w^T*x + b|
当为正例时yi等于1, 当为负例时yi等于-1
为了去除|w^T*x + b|的绝对值,当w^T*x + b > 0 时,yi>0, 当w^T*x + b < 0 时, yi<0, 我们可以将yi * (w^T*x + b) > 0 用来去除绝对值
dist(x, h) = 1/|w| * yi * (w^T*x + b)

优化目标:
找到一条直线w和b使得距离直线最近的点到直线的距离最大

即求得argmax(1/|w| * min(yi * (w^T + b)))
我们对yi * (w^T + b) 进行放缩操作,使得yi * (w ^ T + b) >= 1
那么min(yi * (w^T + b)) 的最小值即为1,上式化解为argmax(1/|w|) 求解这个的最大值,即求解1/2 *w**2 的最小值

这里我们构造拉格朗日乘子法,即求出1/2 * w**2的最大值,约束条件为-(yi*(w^T*x + b))
根据KTT对偶法,先求min max 等价于 max min
f(x) = max min (1/2 * w ** 2 - ai(yi*w^T*x +b - 1) )

先求解最小值,求解∂f(x) / ∂w
∂f(x) / ∂w -= 0 -> w = Σai yi * θ(xi)
∂f(x) / ∂b = 0 -> 0 = Σai yi
将上述得到的结果带入原式中:
L(w, b, a) = 1/2 *|w|^2 - Σai(yi*(w^T*x +b) - 1)
= 1/2 * |w|^2 - w^T*Σai*yi*x +b*Σaiyi - Σai
= Σai - 1/2 * |w| ^ 2
= Σai - 1/2(Σai yi * θ(xi)^T*(Σai yi * θ(xi)
=Σai - 1/2Σaiyiajyi θ(xi)^T*θ(xj)^T

求解什么样的ai使得这个值最大
条件Σaiyi = 0 且拉格朗日法的限制即ai >= 0
对于求解极大值的问题,我们需要将极大值的求解转换为极小值的求解
目标函数 :min 1/2Σaiyiajyi θ(xi)^T*θ(xj)^T - Σai
约束条件:Σaiyi = 0
ai >= 0
SVM求解实例
数据:3个点,其中正例X1(3, 3), X2(4, 3), 负例X3(1, 1)
求解:1/2Σaiyiajyi θ(xi)^T*θ(xj)^T - Σai 的最小值
约束条件 a1 + a2 - a3 = 0
ai >= 0, i = 1, 2, 3

原式: 1/2ΣΣaiajyiyj(xi*xj) - Σai : 将数据带入
1/2(18*a1^2 + 25*a2^2 +2*a3^2 +42*a1*a2 - 12*a1*a2 - 14a2*a3) - a1 - a2 - a3
由于: a1 + a2 = 0 化简可得: 4a1^2 + 13/2*a2^2 + 10*a1*a2 - 2a1 - 2a2

求解上述式子的最小值,对a1进行求导使得偏导等于0,解得a1 = 1.5, a2 = -1 不满足约束条件ai >= 0 ,
因此解在边界上,即a1 = 0 时 a2 = -2/13 代入原式 = -0.153 不满足约束条件
a2 = 0时,a1 = 0.25 代入原式=-0.25 满足约束条件
将a结果带入到w = Σai yi * θ(xi), 解得w = (1/2, 1/2)
b = 1 - w^T * x = 1 - Σai yi * (xi*xj) 选择第一个x1点带入,
= 1 - (1/4 * 1 * 18 + 1/4 * (-1) * 6 ) = -2
平面方程为:0.5x1 +0.5x2 - 2 = 0
从上述的求解我们可以知道,支持向量机表示的是ai不等于0的店,不是支持向量机其他的点都等于0