算法和数据结构一直以来都是程序员的基本内功,可以说没有数据结构的基础建设和算法加持,也就没有这将近八十年的信息革命时代。数据结构可以看作是算法实现的容器,通过一系列特殊结构的数据集合,能够将算法更为高效而可靠地执行起来。
算法的应用不单只体现在编程中。狭义的来讲,算法可看作是数据传递和处理的顺序、方法和组成方式,就像是各种排序算法等。而广义的来讲,算法更像是一种事物运行的逻辑和规则。太阳东升西落,海水潮汐潮流,月儿阴晴圆缺,这些或许都可以看似一种算法,只不过执行者不是电子计算机,而是自然万物。
聊远了。所以对于算法的理解,重要的是领悟其思想,感受其内在。有同学或许就会说了,「算法不就是Leetcode,不就是刷题嘛 」。
片面了啊。题总是刷不完的,但是算法的思想就那么几个。所以呢,刷了那么多题的你,还不了解这几个常见的算法思想,想必是应该好好反省反省下了。
1 枚 举
首先,最为简单的思想,枚举算法。枚举也叫穷举,顾名思义,就是穷尽列举。枚举思想的应用场景十分广泛,也非常容易理解。简单来说,枚举就是将问题的可能解依次列举出来,然后一一带入问题检验,从而从一系列可能解中获得能够解决问题的精确解。
枚举虽然看起来简单,但是其实还是有一些容易被人忽视的考虑点。比方说待解决问题的「可能解/候选解」的筛选条件,「可能解」之间相互的影响,穷举「可能解」的代价,「可能解」的穷举方式等等。
很多时候实际上不必去追求高大上的复杂算法结构,反而大道至简,采用枚举法就能够很好的规避系统复杂性带来的冗余,同时或许在一定程度上还能够对空间进行缩减。
枚举思想的流程可以用下图来表示。通过实现事先确定好「可能解」,然后逐一在系统中进行验证,根据验证结果来对「可能解」进行分析和论证。这是一种很明显的结果导向型的思想,简单粗暴地试图从最终结果反向分析「可能解」的可行性。

不过,枚举思想的劣势当然也很明显。在实际的运行程序中,能够直接通过枚举方法进行求解的问题少之又少。而当「可能解」的筛选条件不清晰,导致「可能解」的数量和范围无法准确判断时,枚举就失去了意义。
然而当「可能解」的规模比较小,同时依次验证的过程容易实施时,枚举思想不失为一种方便快捷的方式。只不过在具体使用时,还可以针对应用场景对「可能解」的验证进行优化。
这种优化可以从两个方向入手,一是问题的简化,尽可能对需要处理的问题进行模型结构上的精简。这种精简具体可体现在问题中的变量数目,减少变量的数据,从而能够从根本上降低「可能解」的组合。
二是对筛选「可能解」的范围和条件进行严格判断,尽可能的剔除大部分无效的「可能解」。
虽说如此,但是一般而言大部分枚举不可用的场景都是由于「可能解」的数量过多,无法在有限空间或有限时间内完成所有可能性的验证。不过实际上枚举思想是最接近人的思维方式,在更多的时候是用来帮助我们去「理解问题」,而不是「解决问题」。
案例
百钱买百鸡问题。 该问题叙述如下:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?
翻译过来,意思是公鸡一个五块钱,母鸡一个三块钱,小鸡三个一块钱,现在要用一百块钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?
2 递 推
递推思想跟枚举思想一样,都是接近人类思维方式的思想,甚至在实际生活具有比枚举思想更多的应用场景。人脑在遇到未知的问题时,大多数人第一直觉都会从积累的「先验知识」出发,试图从「已知」推导「未知」,从而解决问题,说服自己。
事实上,这就是一种递推的算法思想。递推思想的核心就是从已知条件出发,逐步推算出问题的解。实现方式很像是初高中时我们的数学考卷上一连串的「因为」「所以」。那个时候还是用三个点来表示的。
而对于计算机而言,复杂的推导其实很难实现。计算机擅长的是执行高密度重复性高的工作,对于随机性高变化多端的问题反而不好计算。相比之下,人脑在对不同维度的问题进行推导时具有更高的自由度。
比方说,人脑可以很容易的从「太阳从东边升起」推出「太阳从西边落下」,然后大致推出「现在的时间」。但是对于计算机而言并没有那么容易,你可能需要设置一系列的限制条件,才能避免计算机推出「太阳/月亮/星星」从「南/北/东边」「落下/飞走/掉落」的可能性。
我说这个例子的用意是在说明,计算机在运用递推思想时,大多都是重复性的推理。比方说,从「今天是1号」推出「明天是2号」。这种推理的结构十分类似,往往可以通过继而往复的推理就可以得到最终的解。
递推思想用图解来表示可以参见下图。每一次推导的结果可以作为下一次推导的的开始,这似乎跟迭代、递归的思想有点类似,不过递推的范畴要更广一些。
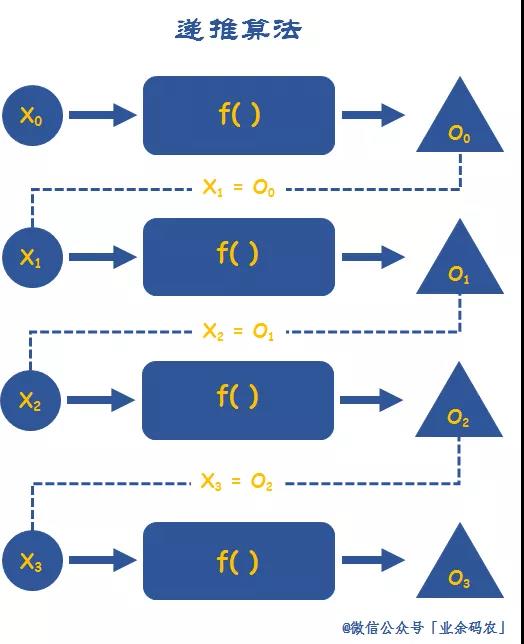
案例
兔子问题。 定一对大兔子每月能生一对小兔子,且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力,如果不发生死亡,且每次均生下一雌一雄,问一年后共有多少对兔子?
3 递 归
说完递推,就不得不说说它的兄弟思想——递归算法。二者同样都带有一个「递」字,可以看出二者还是具有一定的相似性的。「递」的理解可以是逐次、逐步。在递推中,是逐次对问题进行推导直到获得最终解。而在递归中,则是逐次回归迭代,直到跳出回归。
递归算法实际上是把问题转化成规模更小的同类子问题,先解决子问题,再通过相同的求解过程逐步解决更高层次的问题,最终获得最终的解。所以相较于递推而言,递归算法的范畴更小,要求子问题跟父问题的结构相同。而递推思想从概念上并没有这样的约束。
用一句话来形容递归算法的实现,就是在函数或者子过程的内部,直接或间接的调用自己算法。所以在实现的过程中,最重要的是确定递归过程终止的条件,也就是迭代过程跳出的条件判断。否则,程序会在自我调用中无限循环,最终导致内存溢出而崩溃。
递归算法的图解可如下图。很明显,递归思想其实就是一个套娃过程。一般官方都是严禁套娃行为的。所以在使用时一定要明确「套娃」举动的停止条件,及时止损。
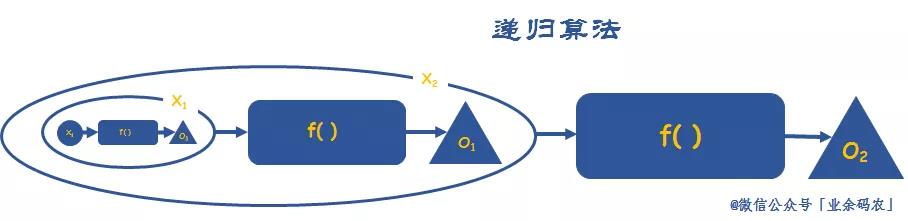
案例
汉诺塔问题。 源于印度传说中,大梵天创造世界时造了三根金钢石柱子,其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
4 分 治
分治,分而治之。
分治算法的核心步骤就是两步,一是分,二是治。但这还引申出了一系列的问题,为什么分,怎么分,怎么治,治后如何。
分治算法很像是一种向下管理的思想,从最高级层层划分,将子任务划分给不同的子模块,进而可以进行大问题的拆分,对系统问题的粒度进行细化,寻求最底层的最基本的解。这样的思路在很多领域都有运用,比如几何数学中的正交坐标、单位坐标、基的概念等,都是通过将复杂问题简化为基本的子问题,然后通过先解决子模块再逐步解决主模块。
在实际的运用中,分治算法主要包括两个维度的处理,一是自顶向下,将主要问题划分逐层级划分为子问题;二是自底向上,将子问题的解逐层递增融入主问题的求解中。
那为什么要分?这个很好解释,由于主要问题的规模过大,无法直接求解,所以需要对主要问题进行粒度划分。
那怎么分?遵循计算机的最擅长的重复运算,划分出来的子问题需要相互独立并且与原问题结构特征相同,这样能够保证解决子问题后,主问题也就能够顺势而解。
怎么治?这就涉及到最基本子问题的求解,我们约定最小的子问题是能够轻易得到解决的,这样的子问题划分才具有意义,所以在治的环节就是需要对最基本子问题的简易求解。
治后如何?子问题的求解是为了主问题而服务的。当最基本的子问题得到解后,需要层层向上递增,逐步获得更高层次问题的解,直到获得原问题的最终解。
分治思想的图解可见下图。通过层层粒度上的划分,将原问题划分为最小的子问题,然后再向上依次得到更高粒度的解。从上而下,再从下而上。先分解,再求解,再合并。
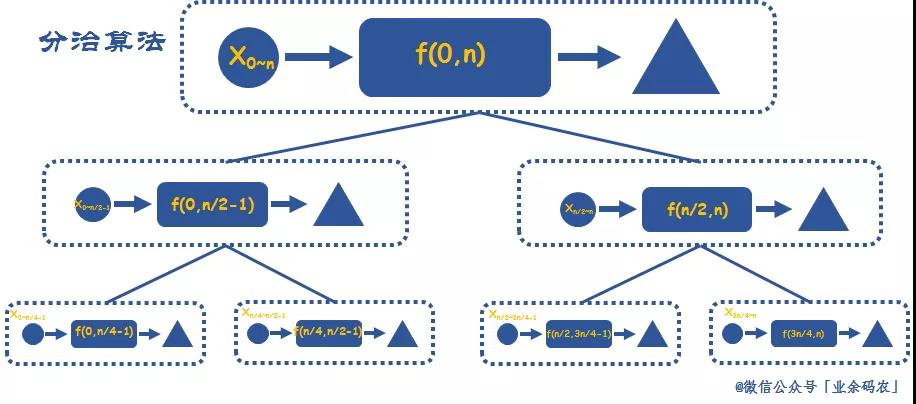
案例
归并排序。
5 动态规划
讲完分治,我们知道分治思想最重要的一点是分解出的子问题是相互独立且结构特征相同的。这一点并不是所有问题都能满足,许多问题的划分的子问题往往都是相互重叠且互相影响的,那么就很难使用分治算法进行有效而又干净的子问题划分。
于是乎,动态规划来了。动态规划同样需要将问题划分为多个子问题,但是子问题之间往往不是互相独立的。当前子问题的解可看作是前多个阶段问题的完整总结。因此这就需要在在子问题求解的过程中进行多阶段的决策,同时当前阶段之前的决策都能够构成一种最优的子结构。这就是所谓的最优化原理。
最优化原理,一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。同时,这样的最优策略是针对有已作出决策的总结,对后来的决策没有直接影响,只能借用目前最优策略的状态数据。这也被称之为无后效性。
动态规划是在目前看来非常不接近人类思维方式一种算法,主要原因是在于人脑在演算的过程中很难对每一次决策的结果进行记忆。动态规划在实际的操作中,往往需要额外的空间对每个阶段的状态数据进行保存,以便下次决策的使用。
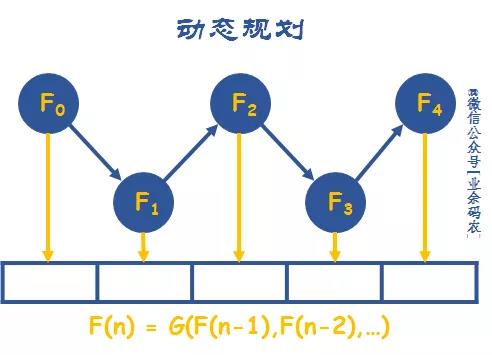
动态规划的求解思路如下图解。动归的开始需要将问题按照一定顺序划分为各个阶段,然后确定每个阶段的状态,如图中节点的F0等。然后重点是根据决策的方法来确定状态转移方程。也就是需要根据当前阶段的状态确定下一阶段的状态。
在这个过程中,下一状态的确定往往需要参考之前的状态。因此需要在每一次状态转移的过程中将当前的状态变量进行记录,方便之后的查找。
动态规划主要就是用来解决多阶段决策的问题,但是实际问题中往往很难有统一的处理方法,必须结合问题的特点来进行算法的设计,这也是这种算法很难真正掌握的原因。
案例
背包问题。 有 n 件物品和容量为 m 的背包,给出物品的重量以及价值。求解让装入背包的物品重量不超过背包容量且价值最大 。
6 贪 心
贪心算法,我愿称之为最现实的算法思想。
人活在世上,不可能每一个选择都那么恰到好处。那么多的问题,不可能所有问题都能找到最优解。很多问题根本没有准确解,甚至于无解。所以在某些场景下,傻傻的去追求问题的最精确解是没有意义的。
有人说,那还有最优解呢。难道最优解都不要了吗?
没错,许多问题虽然找不到最精确的解,但是的确会存在一个或者一些最优解。但是一定要去追求这些最优解吗?我看不一定。
算法的存在不是单纯的为了对问题求解,更多的是提供一种「策略」。何谓「策略」,解决问题的一种方式,一个角度,一条路。所以,贪心思想是有价值的。
说回贪心算法。从贪心二字就可得知,这个算法的目的就是为了「贪图更多」。但是这种贪心是「目光短浅」的,这就导致贪心算法无法从长远出发,只看重眼前的利益。
具体点说,贪心算法在执行的过程中,每一次都会选择最大的收益,但是总收益却不一定最大。所以这样傻白甜的思路带来的好处就是选择简单,不需要纠结,不需要考虑未来。
贪心算法的实现过程就是从问题的一个初始解出发,每一次都作出「当前最优」的选择,直至遇到局部极值点。贪心所带来的局限性很明显,就是无法保证最后的解是最优的,很容易陷入局部最优的情况。
但是它每一次做选择的速度很快,同时判断条件简单,能够比较快速的给出一种差不多的解决方案。这里的图解我用下图来表示。
这个图表示的是求解对多条直线的交点。很显然,下图中的直线是不存在统一交点的,但是可以通过算法求得统一交点的最优解。若是采用贪心算法,那么在进行迭代时,每一次都会选择离此时位置最近的直线进行更新。这样一来,在经过多次迭代后,交点的位置就会在某一片区域无限轮回跳转。而这片区域也就是能求得出的大致的最优解区域。

案例
旅行推销员问题。 给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
7 回 溯
蒹葭苍苍,白露为霜。所谓伊人,在水一方。溯洄从之,道阻且长。溯游从之,宛在水中央。
每每提及回溯,都会忍不住想到「蒹葭」里的这句诗。看到心中所怀念的心上人啊,忍不住逆流而上去追寻她,尽管追随的道路险阻又漫长;又顺流而下继续寻觅,感觉她似乎就在河水中央。回溯算法的过程正如追逐爱情般的艰辛和反复,时而溯洄从之,时而溯游从之。
回溯算法也可称作试探算法,是不是让你回忆起了在女神面前的小心翼翼。简单来说,回溯的过程就是在做出下一步选择之前,先对每一种可能进行试探;只有当可能性存在时才会向前迈进,倘若所有选择都不可能,那么则向后退回原来的位置,重新选择。
这样看起来,回溯算法很像是一种进行中的枚举算法,在行进的过程中对所有可能性进行枚举并判断。常用的应用场景就在对树结构、图结构以及棋盘落子的遍历上。
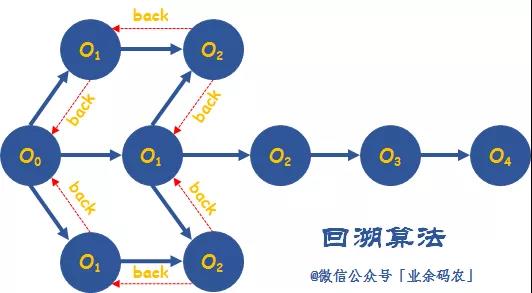
举一个很简单的例子,看下面图解。假设目的是从最O0到达O4,需要对所有节点进行回溯遍历路径。那么回溯算法的过程则需要在前进的每一步对所有可能的路径进行试探。
比方说,O0节点前进的路径有三条,分别是上中下条的O1。回溯过程的开始,先走上面的O1,然后能够到达上面 O2,但是这时是一条死路。那么就需要从O2退回到O1,而此时O1的唯一选择也走不通,所以还需要从O1退回到O0。然后继续试探中间的O1。
回溯算法的过程就是不断进行这样的试探、判断、退回并重新试探,直至找到一条完整的前进路径。只不过在这个过程中,可以通过「剪枝」等限制条件降低试探搜索的空间,从而避免重复无效的试探。比方说上下的O2节点,在经过O0-O1-O2的试探之后,就已经验证了该节点不可行性,下次就无须从O1开始重复对O2的试探。
回溯思想在许多大规模的问题的求解上都能得到有效的运用。回溯能够将复杂问题进行分步调整,从而在中间的过程中可对所有可能运用枚举思想进行遍历。这样往往能够清地看到问题解决的层次,从而可以帮助更好地理解问题的最终解结构。
案例
八皇后问题。 在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
8 模 拟
模拟思想的理解相比上述思想应该不是什么难事。
许多真实场景下,由于问题规模过大,变量过多等因素,很难将具体的问题抽象出来,也就无法针对抽象问题的特征来进行算法的设计。这个时候,模拟思想或许是最佳的解题策略。
模拟的过程就是对真实场景尽可能的模拟,然后通过计算机强大的计算能力对结果进行预测。这相较于上述的算法是一种更为宏大的思想。在进行现实场景的模拟中,可能系统部件的实现都需要上述几个算法思想的参与。
模拟说起来是一种很玄幻的思想,没有具体的实现思路,也没有具体的优化策略。只能说,具体问题具体分析。
那应该怎么样来图解呢。我的理解是自定义的,任意的输入,不规则的系统响应,但是只为了获得一个可靠的理想的输出。
9 总 结
算法思想这种东西,实际上是很玄幻的。同一种问题,或许在实现上可以采用不同的思想进行。这八种思想也不是想象中那么高的独立性,很多思想都是杂糅在一起的,只是角度和侧重点不同。上面这些案例也不代表单只能用一种思想来解答,只是用来体会一下对应的算法思想。
作为底层的程序员,虽说不需要每天刷题,但是基础的算法思想还是需要有的。这种东西不是具体于某个算法,而是在于更高层次的对于系统或者需求的理解。
如独立之精神,自由之思想般。
算法和数据结构一直以来都是程序员的基本内功,可以说没有数据结构的基础建设和算法加持,也就没有这将近八十年的信息革命时代。数据结构可以看作是算法实现的容器,通过一系列特殊结构的数据集合,能够将算法更为高效而可靠地执行起来。
算法的应用不单只体现在编程中。狭义的来讲,算法可看作是数据传递和处理的顺序、方法和组成方式,就像是各种排序算法等。而广义的来讲,算法更像是一种事物运行的逻辑和规则。太阳东升西落,海水潮汐潮流,月儿阴晴圆缺,这些或许都可以看似一种算法,只不过执行者不是电子计算机,而是自然万物。
聊远了。所以对于算法的理解,重要的是领悟其思想,感受其内在。有同学或许就会说了,「算法不就是Leetcode,不就是刷题嘛 」。
片面了啊。题总是刷不完的,但是算法的思想就那么几个。所以呢,刷了那么多题的你,还不了解这几个常见的算法思想,想必是应该好好反省反省下了。
1 枚 举
首先,最为简单的思想,枚举算法。枚举也叫穷举,顾名思义,就是穷尽列举。枚举思想的应用场景十分广泛,也非常容易理解。简单来说,枚举就是将问题的可能解依次列举出来,然后一一带入问题检验,从而从一系列可能解中获得能够解决问题的精确解。
枚举虽然看起来简单,但是其实还是有一些容易被人忽视的考虑点。比方说待解决问题的「可能解/候选解」的筛选条件,「可能解」之间相互的影响,穷举「可能解」的代价,「可能解」的穷举方式等等。
很多时候实际上不必去追求高大上的复杂算法结构,反而大道至简,采用枚举法就能够很好的规避系统复杂性带来的冗余,同时或许在一定程度上还能够对空间进行缩减。
枚举思想的流程可以用下图来表示。通过实现事先确定好「可能解」,然后逐一在系统中进行验证,根据验证结果来对「可能解」进行分析和论证。这是一种很明显的结果导向型的思想,简单粗暴地试图从最终结果反向分析「可能解」的可行性。
不过,枚举思想的劣势当然也很明显。在实际的运行程序中,能够直接通过枚举方法进行求解的问题少之又少。而当「可能解」的筛选条件不清晰,导致「可能解」的数量和范围无法准确判断时,枚举就失去了意义。
然而当「可能解」的规模比较小,同时依次验证的过程容易实施时,枚举思想不失为一种方便快捷的方式。只不过在具体使用时,还可以针对应用场景对「可能解」的验证进行优化。
这种优化可以从两个方向入手,一是问题的简化,尽可能对需要处理的问题进行模型结构上的精简。这种精简具体可体现在问题中的变量数目,减少变量的数据,从而能够从根本上降低「可能解」的组合。
二是对筛选「可能解」的范围和条件进行严格判断,尽可能的剔除大部分无效的「可能解」。
虽说如此,但是一般而言大部分枚举不可用的场景都是由于「可能解」的数量过多,无法在有限空间或有限时间内完成所有可能性的验证。不过实际上枚举思想是最接近人的思维方式,在更多的时候是用来帮助我们去「理解问题」,而不是「解决问题」。
案例
百钱买百鸡问题。 该问题叙述如下:鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?
翻译过来,意思是公鸡一个五块钱,母鸡一个三块钱,小鸡三个一块钱,现在要用一百块钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?
2 递 推
递推思想跟枚举思想一样,都是接近人类思维方式的思想,甚至在实际生活具有比枚举思想更多的应用场景。人脑在遇到未知的问题时,大多数人第一直觉都会从积累的「先验知识」出发,试图从「已知」推导「未知」,从而解决问题,说服自己。
事实上,这就是一种递推的算法思想。递推思想的核心就是从已知条件出发,逐步推算出问题的解。实现方式很像是初高中时我们的数学考卷上一连串的「因为」「所以」。那个时候还是用三个点来表示的。
而对于计算机而言,复杂的推导其实很难实现。计算机擅长的是执行高密度重复性高的工作,对于随机性高变化多端的问题反而不好计算。相比之下,人脑在对不同维度的问题进行推导时具有更高的自由度。
比方说,人脑可以很容易的从「太阳从东边升起」推出「太阳从西边落下」,然后大致推出「现在的时间」。但是对于计算机而言并没有那么容易,你可能需要设置一系列的限制条件,才能避免计算机推出「太阳/月亮/星星」从「南/北/东边」「落下/飞走/掉落」的可能性。
我说这个例子的用意是在说明,计算机在运用递推思想时,大多都是重复性的推理。比方说,从「今天是1号」推出「明天是2号」。这种推理的结构十分类似,往往可以通过继而往复的推理就可以得到最终的解。
递推思想用图解来表示可以参见下图。每一次推导的结果可以作为下一次推导的的开始,这似乎跟迭代、递归的思想有点类似,不过递推的范畴要更广一些。
案例
兔子问题。 定一对大兔子每月能生一对小兔子,且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力,如果不发生死亡,且每次均生下一雌一雄,问一年后共有多少对兔子?
3 递 归
说完递推,就不得不说说它的兄弟思想——递归算法。二者同样都带有一个「递」字,可以看出二者还是具有一定的相似性的。「递」的理解可以是逐次、逐步。在递推中,是逐次对问题进行推导直到获得最终解。而在递归中,则是逐次回归迭代,直到跳出回归。
递归算法实际上是把问题转化成规模更小的同类子问题,先解决子问题,再通过相同的求解过程逐步解决更高层次的问题,最终获得最终的解。所以相较于递推而言,递归算法的范畴更小,要求子问题跟父问题的结构相同。而递推思想从概念上并没有这样的约束。
用一句话来形容递归算法的实现,就是在函数或者子过程的内部,直接或间接的调用自己算法。所以在实现的过程中,最重要的是确定递归过程终止的条件,也就是迭代过程跳出的条件判断。否则,程序会在自我调用中无限循环,最终导致内存溢出而崩溃。
递归算法的图解可如下图。很明显,递归思想其实就是一个套娃过程。一般官方都是严禁套娃行为的。所以在使用时一定要明确「套娃」举动的停止条件,及时止损。
案例
汉诺塔问题。 源于印度传说中,大梵天创造世界时造了三根金钢石柱子,其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
4 分 治
分治,分而治之。
分治算法的核心步骤就是两步,一是分,二是治。但这还引申出了一系列的问题,为什么分,怎么分,怎么治,治后如何。
分治算法很像是一种向下管理的思想,从最高级层层划分,将子任务划分给不同的子模块,进而可以进行大问题的拆分,对系统问题的粒度进行细化,寻求最底层的最基本的解。这样的思路在很多领域都有运用,比如几何数学中的正交坐标、单位坐标、基的概念等,都是通过将复杂问题简化为基本的子问题,然后通过先解决子模块再逐步解决主模块。
在实际的运用中,分治算法主要包括两个维度的处理,一是自顶向下,将主要问题划分逐层级划分为子问题;二是自底向上,将子问题的解逐层递增融入主问题的求解中。
那为什么要分?这个很好解释,由于主要问题的规模过大,无法直接求解,所以需要对主要问题进行粒度划分。
那怎么分?遵循计算机的最擅长的重复运算,划分出来的子问题需要相互独立并且与原问题结构特征相同,这样能够保证解决子问题后,主问题也就能够顺势而解。
怎么治?这就涉及到最基本子问题的求解,我们约定最小的子问题是能够轻易得到解决的,这样的子问题划分才具有意义,所以在治的环节就是需要对最基本子问题的简易求解。
治后如何?子问题的求解是为了主问题而服务的。当最基本的子问题得到解后,需要层层向上递增,逐步获得更高层次问题的解,直到获得原问题的最终解。
分治思想的图解可见下图。通过层层粒度上的划分,将原问题划分为最小的子问题,然后再向上依次得到更高粒度的解。从上而下,再从下而上。先分解,再求解,再合并。
案例
归并排序。
5 动态规划
讲完分治,我们知道分治思想最重要的一点是分解出的子问题是相互独立且结构特征相同的。这一点并不是所有问题都能满足,许多问题的划分的子问题往往都是相互重叠且互相影响的,那么就很难使用分治算法进行有效而又干净的子问题划分。
于是乎,动态规划来了。动态规划同样需要将问题划分为多个子问题,但是子问题之间往往不是互相独立的。当前子问题的解可看作是前多个阶段问题的完整总结。因此这就需要在在子问题求解的过程中进行多阶段的决策,同时当前阶段之前的决策都能够构成一种最优的子结构。这就是所谓的最优化原理。
最优化原理,一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。同时,这样的最优策略是针对有已作出决策的总结,对后来的决策没有直接影响,只能借用目前最优策略的状态数据。这也被称之为无后效性。
动态规划是在目前看来非常不接近人类思维方式一种算法,主要原因是在于人脑在演算的过程中很难对每一次决策的结果进行记忆。动态规划在实际的操作中,往往需要额外的空间对每个阶段的状态数据进行保存,以便下次决策的使用。
动态规划的求解思路如下图解。动归的开始需要将问题按照一定顺序划分为各个阶段,然后确定每个阶段的状态,如图中节点的F0等。然后重点是根据决策的方法来确定状态转移方程。也就是需要根据当前阶段的状态确定下一阶段的状态。
在这个过程中,下一状态的确定往往需要参考之前的状态。因此需要在每一次状态转移的过程中将当前的状态变量进行记录,方便之后的查找。
动态规划主要就是用来解决多阶段决策的问题,但是实际问题中往往很难有统一的处理方法,必须结合问题的特点来进行算法的设计,这也是这种算法很难真正掌握的原因。
案例
背包问题。 有 n 件物品和容量为 m 的背包,给出物品的重量以及价值。求解让装入背包的物品重量不超过背包容量且价值最大 。
6 贪 心
贪心算法,我愿称之为最现实的算法思想。
人活在世上,不可能每一个选择都那么恰到好处。那么多的问题,不可能所有问题都能找到最优解。很多问题根本没有准确解,甚至于无解。所以在某些场景下,傻傻的去追求问题的最精确解是没有意义的。
有人说,那还有最优解呢。难道最优解都不要了吗?
没错,许多问题虽然找不到最精确的解,但是的确会存在一个或者一些最优解。但是一定要去追求这些最优解吗?我看不一定。
算法的存在不是单纯的为了对问题求解,更多的是提供一种「策略」。何谓「策略」,解决问题的一种方式,一个角度,一条路。所以,贪心思想是有价值的。
说回贪心算法。从贪心二字就可得知,这个算法的目的就是为了「贪图更多」。但是这种贪心是「目光短浅」的,这就导致贪心算法无法从长远出发,只看重眼前的利益。
具体点说,贪心算法在执行的过程中,每一次都会选择最大的收益,但是总收益却不一定最大。所以这样傻白甜的思路带来的好处就是选择简单,不需要纠结,不需要考虑未来。
贪心算法的实现过程就是从问题的一个初始解出发,每一次都作出「当前最优」的选择,直至遇到局部极值点。贪心所带来的局限性很明显,就是无法保证最后的解是最优的,很容易陷入局部最优的情况。
但是它每一次做选择的速度很快,同时判断条件简单,能够比较快速的给出一种差不多的解决方案。这里的图解我用下图来表示。
这个图表示的是求解对多条直线的交点。很显然,下图中的直线是不存在统一交点的,但是可以通过算法求得统一交点的最优解。若是采用贪心算法,那么在进行迭代时,每一次都会选择离此时位置最近的直线进行更新。这样一来,在经过多次迭代后,交点的位置就会在某一片区域无限轮回跳转。而这片区域也就是能求得出的大致的最优解区域。
案例
旅行推销员问题。 给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
7 回 溯
蒹葭苍苍,白露为霜。所谓伊人,在水一方。溯洄从之,道阻且长。溯游从之,宛在水中央。
每每提及回溯,都会忍不住想到「蒹葭」里的这句诗。看到心中所怀念的心上人啊,忍不住逆流而上去追寻她,尽管追随的道路险阻又漫长;又顺流而下继续寻觅,感觉她似乎就在河水中央。回溯算法的过程正如追逐爱情般的艰辛和反复,时而溯洄从之,时而溯游从之。
回溯算法也可称作试探算法,是不是让你回忆起了在女神面前的小心翼翼。简单来说,回溯的过程就是在做出下一步选择之前,先对每一种可能进行试探;只有当可能性存在时才会向前迈进,倘若所有选择都不可能,那么则向后退回原来的位置,重新选择。
这样看起来,回溯算法很像是一种进行中的枚举算法,在行进的过程中对所有可能性进行枚举并判断。常用的应用场景就在对树结构、图结构以及棋盘落子的遍历上。
举一个很简单的例子,看下面图解。假设目的是从最O0到达O4,需要对所有节点进行回溯遍历路径。那么回溯算法的过程则需要在前进的每一步对所有可能的路径进行试探。
比方说,O0节点前进的路径有三条,分别是上中下条的O1。回溯过程的开始,先走上面的O1,然后能够到达上面 O2,但是这时是一条死路。那么就需要从O2退回到O1,而此时O1的唯一选择也走不通,所以还需要从O1退回到O0。然后继续试探中间的O1。
回溯算法的过程就是不断进行这样的试探、判断、退回并重新试探,直至找到一条完整的前进路径。只不过在这个过程中,可以通过「剪枝」等限制条件降低试探搜索的空间,从而避免重复无效的试探。比方说上下的O2节点,在经过O0-O1-O2的试探之后,就已经验证了该节点不可行性,下次就无须从O1开始重复对O2的试探。
回溯思想在许多大规模的问题的求解上都能得到有效的运用。回溯能够将复杂问题进行分步调整,从而在中间的过程中可对所有可能运用枚举思想进行遍历。这样往往能够清地看到问题解决的层次,从而可以帮助更好地理解问题的最终解结构。
案例
八皇后问题。 在8×8格的国际象棋上摆放8个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
8 模 拟
模拟思想的理解相比上述思想应该不是什么难事。
许多真实场景下,由于问题规模过大,变量过多等因素,很难将具体的问题抽象出来,也就无法针对抽象问题的特征来进行算法的设计。这个时候,模拟思想或许是最佳的解题策略。
模拟的过程就是对真实场景尽可能的模拟,然后通过计算机强大的计算能力对结果进行预测。这相较于上述的算法是一种更为宏大的思想。在进行现实场景的模拟中,可能系统部件的实现都需要上述几个算法思想的参与。
模拟说起来是一种很玄幻的思想,没有具体的实现思路,也没有具体的优化策略。只能说,具体问题具体分析。
那应该怎么样来图解呢。我的理解是自定义的,任意的输入,不规则的系统响应,但是只为了获得一个可靠的理想的输出。
9 总 结
算法思想这种东西,实际上是很玄幻的。同一种问题,或许在实现上可以采用不同的思想进行。这八种思想也不是想象中那么高的独立性,很多思想都是杂糅在一起的,只是角度和侧重点不同。上面这些案例也不代表单只能用一种思想来解答,只是用来体会一下对应的算法思想。
作为底层的程序员,虽说不需要每天刷题,但是基础的算法思想还是需要有的。这种东西不是具体于某个算法,而是在于更高层次的对于系统或者需求的理解。
如独立之精神,自由之思想般。