虚树学习笔记

文章来自：https://blog.sengxian.com/algorithms/virtual-tree

本文由于格式问题，插图需要重新打开来看。

概述

在 OI 比赛中，有这样一类题目：给定一棵树，另有多次询问，每个询问给定一些关键点，需要求这些关键点之间的某些信息。询问数可能很多，但满足所有询问中关键点数量的总和与树的大小同阶。

由于询问数可以非常多，每次无法遍历整棵树，这类题目看似没有办法做，但实际上，我们可以用一种叫做虚树（virtual tree）的技术来解决这一问题。

介绍

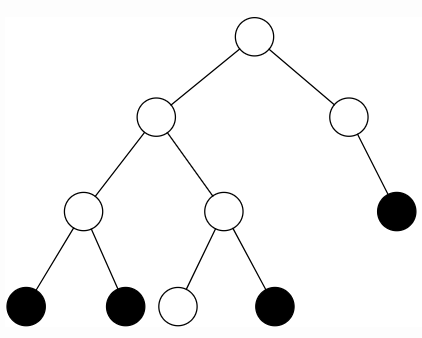
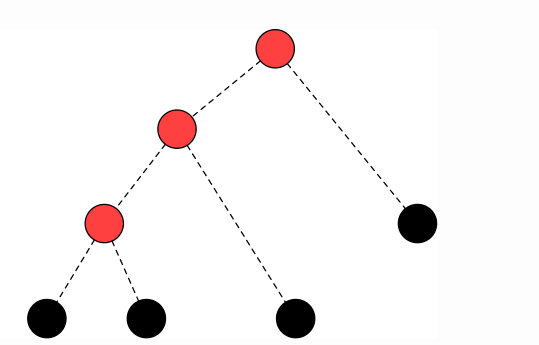
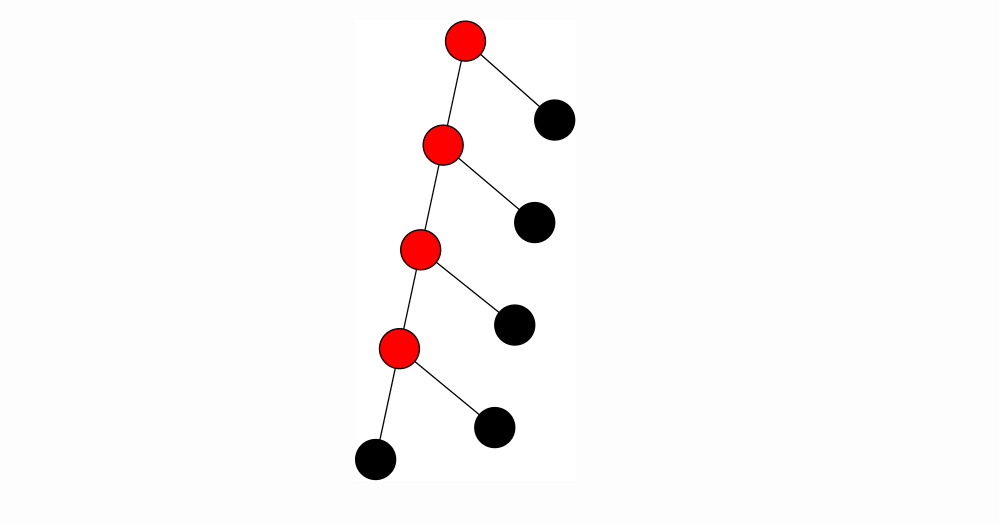
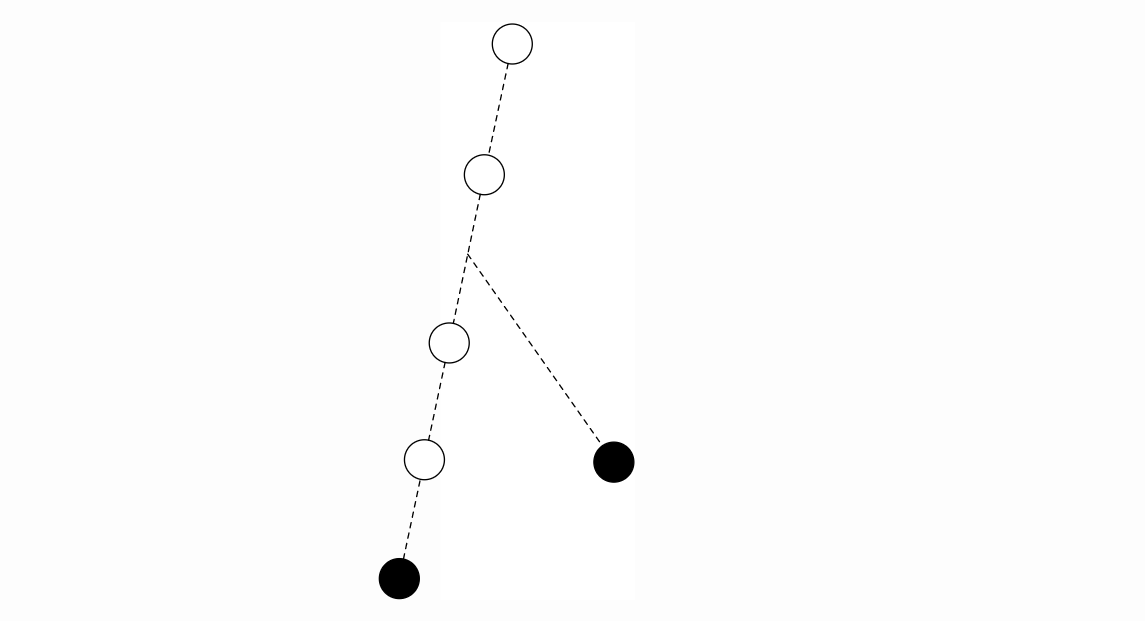
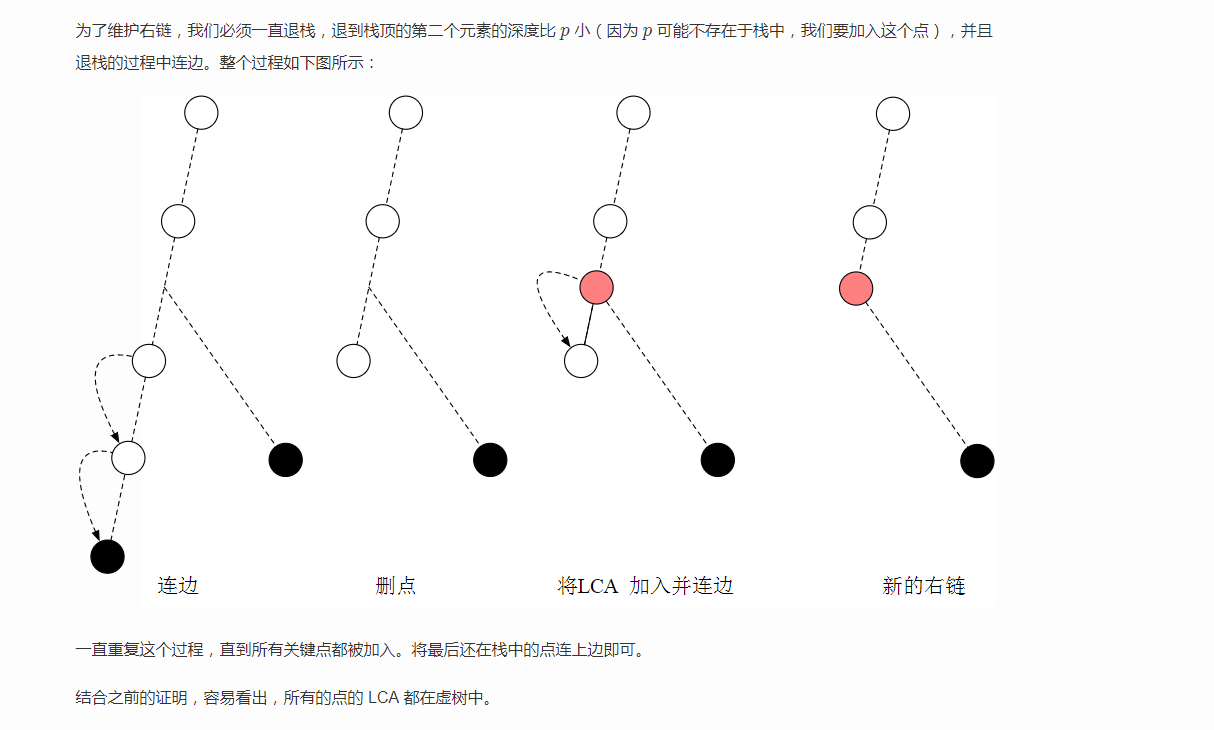
简单来说，虚树是对一颗有根树中的一些关键点而言的，虚树将树的大小压缩到与关键点的数量同阶。虚树中包含了所有的关键点，也包含了所有关键点两两之间的 LCA（lowest common ancestor, 最近公共祖先）（LCA 的数量不超过关键点的个数，稍后有证明），这就保证了虚树不会丧失原有的树形结构，同时尽可能地压缩了树的大小。同时虚树中 u 到 v 的边权定义为原树中 u到 v 的最短路径。

我们看一个虚树的例子（黑色点为关键点，红色点为 LCA）：

 

　　代码:

inline bool cmp(const int &i, const int &j) {
    return dfn[i] < dfn[j];
}

void build(int vectrices[], int k) {
    static int stk[MAX_N];
    sort(vectrices, vectrices + k, cmp);

    stk[sz++] = 0;
    for (int i = 0; i < k; ++i) {
        int u = vectrices[i], lca = ::lca(u, stk[sz - 1]);
        if (lca == stk[sz - 1]) stk[sz++] = u;
        else {
            while (sz - 2 >= 0 && dep[stk[sz - 2]] >= dep[lca]) {
                addEdge(stk[sz - 2], stk[sz - 1]);
                sz--;
            }

            if (stk[sz - 1] != lca) {
                addEdge(lca, stk[--sz]);
                stk[sz++] = lca, vectrices[cnt++] = lca;
            }

            stk[sz++] = u;
        }
    }
    for (int i = 0; i < sz - 1; ++i) addEdge(stk[i], stk[i + 1]);

　　例题：BZOJ 2286
BZOJ 3572
BZOJ 3991