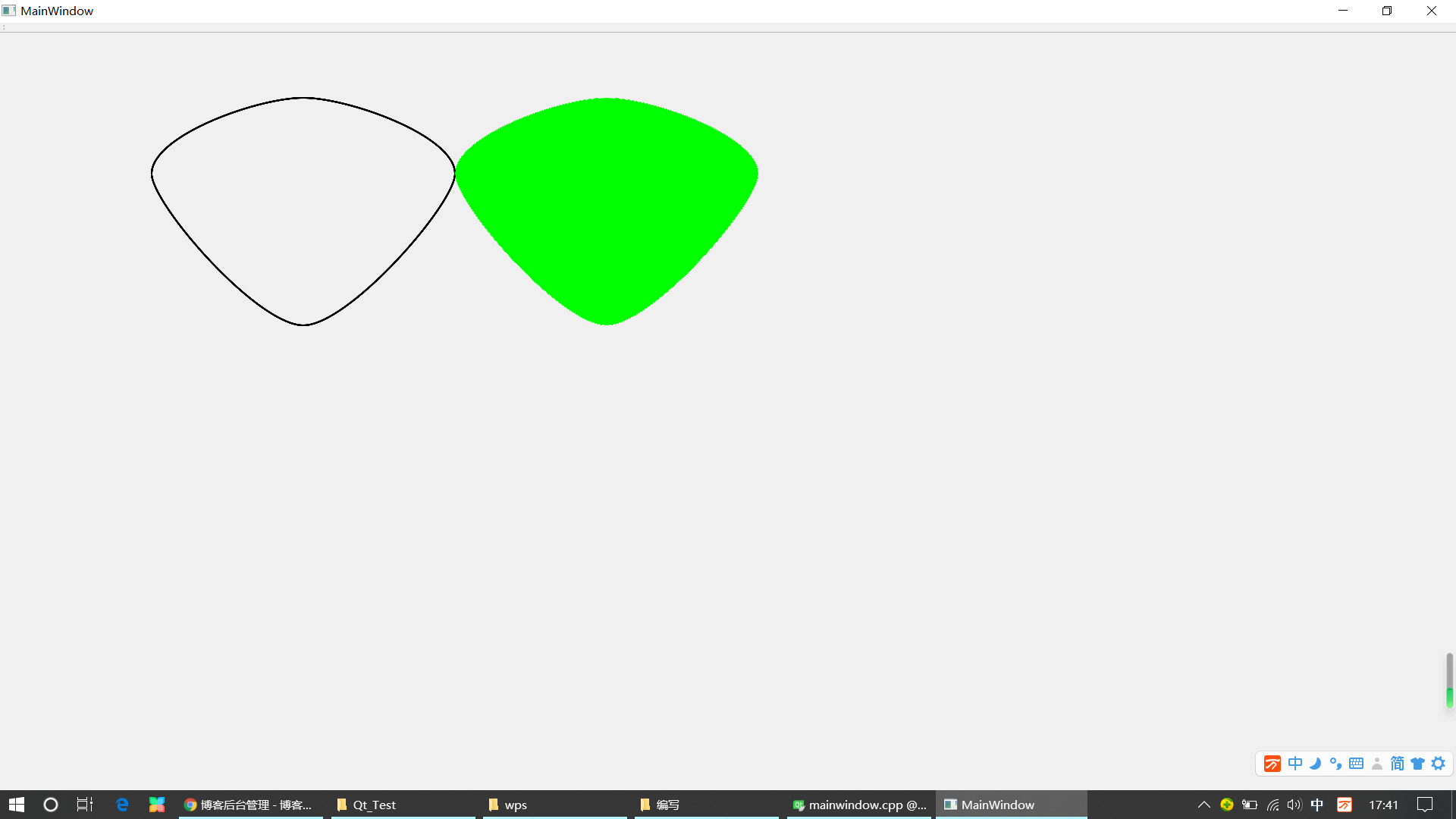
绘制过多点的曲线意义重大。但通过试验,QT的PainterPath不是很如意。当多段曲线围成一个区域时,PainterPath内并不包含该区域的所有面积,只包含曲线和其弦构成的面积。
为了解决这一问题,采用如下方法:
1. 生成自己的bezier曲线点集
2. 将多个bezier曲线头尾相联,形成整个polygon的点集
3. 将这个polygon放入一个PainterPath,然后绘制;
4. 这个PainterPath返回留待下次使用。
下面是代码:
1. 头文件graphic.h
#ifndef GRAPHIC_H
#define GRAPHIC_H
#include <QPainter>
#include <QPoint>
#include <QColor>
#include <QVector>
//step是步长,即t每次的递增量,traceSet返回本曲线的所有生成点
void getBezier3(const QPointF& startPos, const QPointF& controlPos1, const QPointF& controlPos2, const QPointF& endPos,
const double step, QVector<QPointF>& traceSet);
//画一个多边形的外接曲线,points是多边形的顶点集合,方向是CCW或CW;k_c是连接处的尖锐度,越大越光滑,通常选0.6;path是返回量,它是一个包含了外接曲线所有点的多边形区域,可用于
//测试一个点是否在这个区域内,或两个区域是否相交等,还可以完成path的绘制。
void drawEncloseCurve(QPainter& painter, const QVector<QPoint>& points, float k_c, const QColor& color, int strokWidth, QPainterPath& path);
#endif // GRAPHIC_H
2. 绘制实现graphic.cpp
#include "graphic.h"
//求两点距离
double distance(const QPoint& p1, const QPoint& p2)
{
return sqrt(((p1.x() - p2.x()) * (p1.x() - p2.x()) + (p1.y() - p2.y()) * (p1.y() - p2.y())));
}
//根据比例调整点的位置
QPoint ratioPointConvert(const QPoint& p1, const QPoint& p2, const double ratio)
{
QPoint p;
p.setX((int) (ratio * (p1.x() - p2.x()) + p2.x()));
p.setY((int) (ratio * (p1.y() - p2.y()) + p2.y()));
return p;
}
void getBezier3(const QPointF& startPos, const QPointF& controlPos1, const QPointF& controlPos2, const QPointF& endPos,
const double step, QVector<QPointF>& traceSet)
{
double t = 0.0;
double x_t, y_t;
while (t <= 1.0) {
x_t = startPos.x() * (1 - t) * (1 - t) * (1 - t) + 3 * controlPos1.x() * t * (1 - t) * (1 - t) + 3 * controlPos2.x() * t * t * (1 - t) + endPos.x() * t * t * t;
y_t = startPos.y() * (1 - t) * (1 - t) * (1 - t) + 3 * controlPos1.y() * t * (1 - t) * (1 - t) + 3 * controlPos2.y() * t * t * (1 - t) + endPos.y() * t * t * t;
traceSet.push_back(QPointF(x_t, y_t));
t += step;
}
}
void drawEncloseCurve(QPainter& painter, const QVector<QPoint>& points, float k_c, const QColor& color, int strokWidth, QPainterPath& path)
{
//path.clear();
int size = points.size();
QVector<QPoint> midpoints;
// 计算中点
for(int i = 0; i < size; i++)
{
int j = (i + 1) % size;
midpoints.push_back(QPoint((points[i].x() + points[j].x()) / 2, (points[i].y() + points[j].y()) / 2));
}
// 计算比例点
QVector<QPoint> ratioPoints;
for(int i = 0; i < size; i++)
{
int j = (i + 1) % size;
int m = (i + 2) % size;
double l1 = distance(points[i], points[j]);
double l2 = distance(points[j], points[m]);
double ratio = l1 / (l1 + l2);
ratioPoints.push_back(ratioPointConvert(midpoints[i], midpoints[j], ratio));
}
// 移动线段,计算控制点
QVector<QPoint> controlPoints;
for (int i = 0; i < size; i++)
{
QPoint ratioPoint = ratioPoints[i];
QPoint verPoint = points[(i + 1) % size];
int dx = ratioPoint.x() - verPoint.x();
int dy = ratioPoint.y() - verPoint.y();
QPoint controlPoint1 = QPoint(midpoints[i].x() - dx, midpoints[i].y() - dy);
QPoint controlPoint2 = QPoint(midpoints[(i + 1) % size].x() - dx, midpoints[(i + 1) % size].y() - dy);
controlPoints.push_back(ratioPointConvert(controlPoint1, verPoint, k_c));
controlPoints.push_back(ratioPointConvert(controlPoint2, verPoint, k_c));
}
// 用三阶贝塞尔曲线连接顶点
//QPainterPath path;
QVector<QPointF> polypoints;
QPen pen;
pen.setColor(color);
pen.setWidth(strokWidth);
pen.setCapStyle(Qt::RoundCap);
pen.setJoinStyle(Qt::RoundJoin);
painter.setPen(pen);
for (int i = 0; i < size; i++)
{
QPoint startPoint = points[i];
QPoint endPoint = points[(i + 1) % size];
QPoint controlPoint1 = controlPoints[(i * 2 + controlPoints.size() - 1) % controlPoints.size()];
QPoint controlPoint2 = controlPoints[(i * 2) % controlPoints.size()];
// path.moveTo(startPoint.x(), startPoint.y());
// path.cubicTo(controlPoint1.x(), controlPoint1.y(), controlPoint2.x(), controlPoint2.y(), endPoint.x(), endPoint.y());
QVector<QPointF> bezier;
getBezier3(startPoint, controlPoint1, controlPoint2, endPoint, 0.01, bezier);
bezier.removeLast();
polypoints += bezier;
}
QPolygonF poly(polypoints);
path.addPolygon(poly);
painter.drawPath(path);
}
3. 测试(mainwindow.cpp)
测试时发现了问题:当Qdebug()<< 输入中文时,调试直接跳走,无法继续步进,但如果改成英文,则没有问题。
void MainWindow::paintEvent(QPaintEvent *event)
{
QPainter painter(this);
//绘制封闭的外接曲线
painter.setRenderHint(QPainter::Antialiasing, true);
QVector<QPoint> points;
points.push_back(QPoint(200, 200));
points.push_back(QPoint(400, 100));
points.push_back(QPoint(600, 200));
points.push_back(QPoint(400, 400));
drawEncloseCurve(painter, points, 0.6, QColor(Qt::black), 2, npath);
painter.save();
painter.translate(400, 0);
painter.fillPath(npath, QBrush(Qt::green));
painter.restore();
}
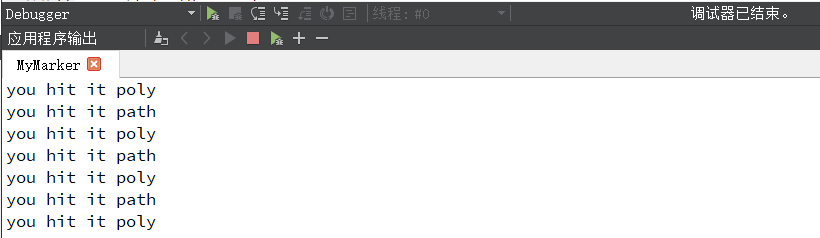
测试鼠标是否在这个区域中
void MainWindow::mousePressEvent(QMouseEvent *event)
{
if(event->button() == Qt::LeftButton)
{
QPointF p = event->pos();
if(npath.contains(p))
qDebug() << ("you hit it path");
//通过试验,有时用npath测试无效,但poly总是有效
QPolygonF poly = npath.toFillPolygon();
if(poly.containsPoint(p, Qt::WindingFill))
{
qDebug() << ("you hit it poly");
startDrawing = false;
}
else
{
startDrawing = true;
startPos = event->pos();
}
}
}
4.结果:
通过四个点的封闭曲线,并通过了鼠标选取测试