一 介绍
对于数据处理来说,整个处理的流程如下图所示:

数据预处理——通常包括特征选择、维规约、规范化等方法。
数据挖掘——这部分的方法和技术非常多,在处理时主要根据自己的目的来选择对应的方法最为恰当。
数据后处理——主要包括模式过滤、可视化等,目的是为了让数据挖掘的结果利于使用和观察。
为了让大家有一个清晰的框架,后面内容的思维导图如下展示:
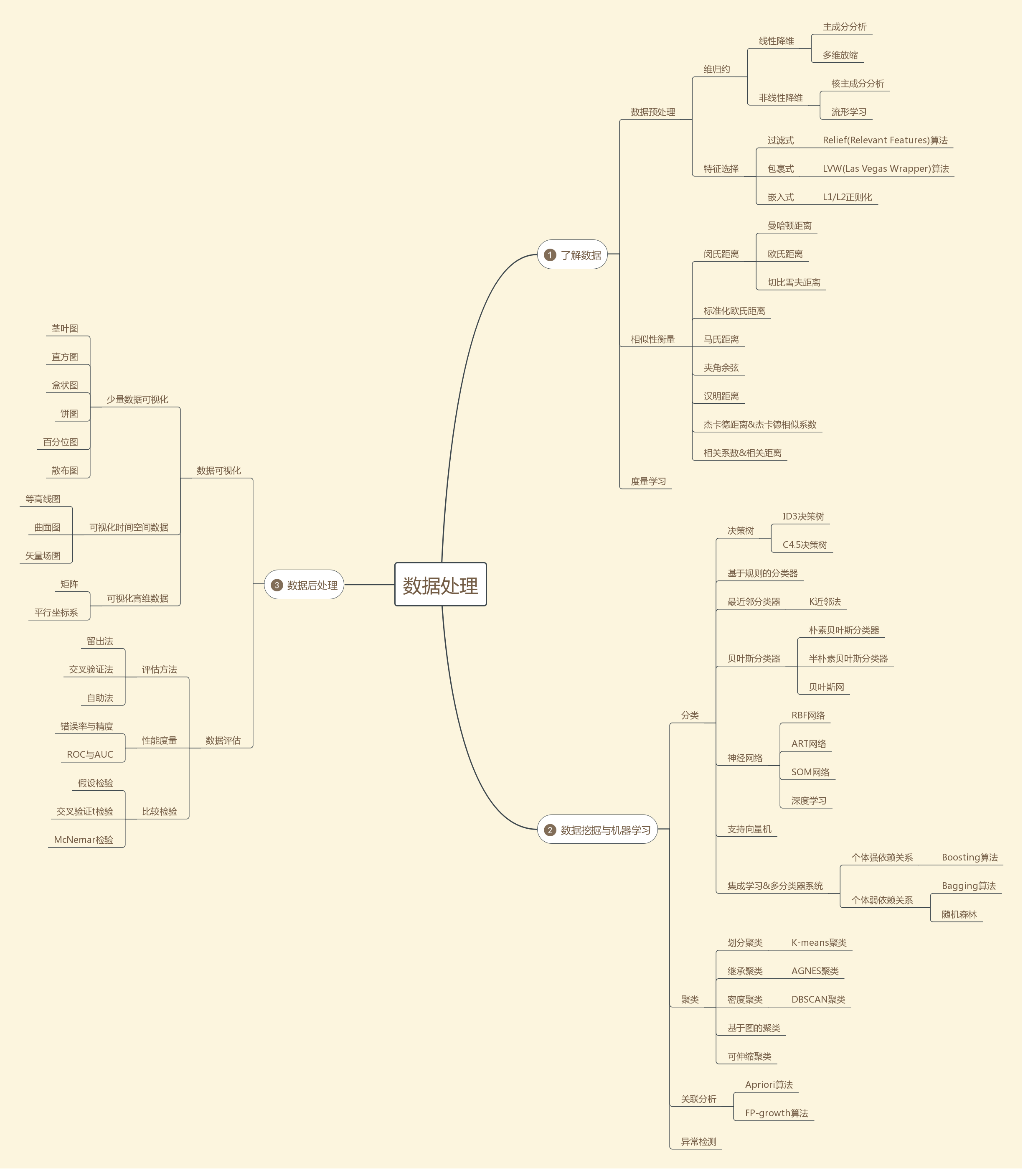
二 了解数据
数据处理最关键的地方在于解决问题,并不是使用的方法越复杂越好。无论方法多么简单,只要解决问题就是好的方法。为了解决数据处理的相关问题,第一步是观察数据,了解数据相关的概念,然后对数据进行一些处理。这样对后面具体使用哪个方法来进行分析非常有用。
2.1数据预处理
数据预处理对于后续使用数据挖掘或者机器学习技术非常重要。在面临大数据的当下,数据的维度通常非常的多,因此数据预处理的一个主要任务就是降低数据维度。
2.1.1维归约
所谓维归约,就是要减少数据的特征数目,摒弃掉不重要的特征,尽量只用少数的关键特征来描述数据。人们总是希望看到的现象主要是由少数的关键特征造成的,找到这些关键特征也是数据分析的目的。维归约中主要方法很多,下面介绍几个:
(1)主成分分析
主成分分析是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
主成分分析的基本解决的问题是:正交属性空间中的样本点,如何使用一个超平面对所有样本进行恰当的表达?若存在这样的超平面,那么它大概应具有这样的性质:
最近重构性:样本点到这个超平面的距离都足够近。
最大可分性:样本点在这个超平面上的投影能尽可能分开。
根据这两个性质即可得到主成分分析的两种等价推导。
优点:
1、 可消除评价指标之间的相关影响,因为主成分分析在对原指标变量进行变换后形成了彼此相互独立的主成分,而且实践证明指标之间相关程度越高,主成分分析效果越好。
2、 可减少指标选择的工作量,对于其它评价方法,由于难以消除评价指标间的相关影响,所以选择指标时要花费不少精力,而主成分分析由于可以消除这种相关影响,所以在指标选择上相对容易些。
3、 当评级指标较多时还可以在保留绝大部分信息的情况下用少数几个综合指标代替原指标。
缺点:
1.在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平(即变量降维后的信息量须保持在一个较高水平上),其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释(否则主成分将空有信息量而无实际含义)。
2.主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。因此,提取的主成分个数m通常应明显小于原始变量个数p(除非p本身较小),否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。
3.只能处理线性降维。
(2)核主成分分析
线性降维方法假设从高维空间到低维空间的函数映射是线性的,然而在不少现实任务中,可能需要非线性映射才能找到恰当的低维嵌入。如果直接使用线性降维的方式,有可能使得数据丧失原有的低维结构。非线性降维的一种常用方法是,基于核技巧对线性降维方法进行“核化”。
(3)流形学习
流形学习是一类借鉴了拓扑流形概念的降维方法。“流形”是在局部与欧氏空间同胚的空间,换言之,它在局部具有欧氏空间的性质,能用欧氏距离进行距离的计算。这给降维方法带来了启发:若低维流形嵌入到高维空间,则数据样本在高维空间中的分布虽然比较复杂,但在局部上仍具有欧氏空间的性质。因此,可以容易的在局部建立降维映射关系,然后设法将局部映射关系推广到全局。
(4)多维缩放(Multiple Dimensional Scaling, MDS)
多维缩放是一种降维方法,要求原始空间中样本之间的距离在低维空间中得以保持。
2.1.2特征选择
特征选择( Feature Selection )也称特征子集选择( Feature Subset Selection , FSS ),或属性选择( Attribute Selection )。是指从已有的M个特征(Feature)中选择N个特征使得系统的特定指标最优化,是从原始特征中选择出一些最有效特征以降低数据集维度的过程,是提高学习算法性能的一个重要手段,也是模式识别中关键的数据预处理步骤。对于一个学习算法来说,好的学习样本是训练模型的关键。搜索策略可大致分为以下3类:
(1)过滤式
Relief(Relevant Features)算法
(2)包裹式
LVW(Las Vegas Wrapper)算法
(3)嵌入式
L1/L2 正则化
思考:
特征选择也是一种降维方式,但是它处理的方式和主成分分析有区别,它直接删除了某些特征。而主成分分析的每个特征都是其他特征的线性组合。
2.2相似性衡量
在做分类或者聚类任务时常常需要估算不同样本之间的相似性度量(Similarity Measurement),这时通常采用的方法就是计算样本间的“距离”(Distance)。采用什么样的方法计算距离是很讲究,甚至关系到分类的正确与否。下面就是对常用的相似性度量作一个总结。
2.2.1 闵可夫斯基距离
闵氏距离不是一种距离,而是一组距离的定义。
缺点主要有两个:
(1) 将各个分量的量纲(scale),也就是“单位”当作相同的看待了。
(2) 没有考虑各个分量的分布(期望,方差等)可能是不同的。
2.2.2 标准化欧氏距离
标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路:数据各维分量的分布不一样,因此先将各个分量都“标准化”到均值、方差相等。
如果将方差的倒数看成是一个权重,这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。
2.2.3 马氏距离
马氏距离的优缺点:量纲无关,排除变量之间的相关性的干扰。
2.2.4 夹角余弦
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异。
2.2.5 汉明距离
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
应用:信息编码(为了增强容错性,应使得编码间的最小汉明距离尽可能大)。
2.2.6 杰卡德距离&杰卡德相似系数
2.2.7 相关系数&相关距离
2.3 度量学习
在机器学习中,对高维数据进行降维的主要目标是希望找到一个合适的低维空间,在此空间中进行学习能比原始空间性能更好。事实上,每个空间对应了在样本属性上定义的一个距离度量,而寻找合适的空间,本质上就是在寻找一个合适的距离度量。因此,度量学习提出了直接学习出一个合适的距离度量的方案。
三 数据挖掘与机器学习
在进行完数据探索和预处理后,可能需要对自己的目标数据选择具体的方法来进行进一步分析。数据探索的动机通常是对数据进行分类、聚类和关联分析以及异常检测,因此下面的方法和技术按照这个顺序介绍。
3.1分类
分类的方法多种多样,具体来说,有下面介绍的主要方法。
3.1.1决策树
**思考:**决策树的决策过程非常直观,容易被人理解,因此其除了可以用于分类外,也可用于可视化,因为决策树的结果很容易做成图,结果比较清晰。
3.1.2 基于规则的分类器
基于规则的分类器是使用一组“if…then…”规则来对记录进行分类的技术。
**思考:**基于规则的分类器是最好有创新点的分类方法,因为规则都是自己定的。
3.1.3最近邻分类器
3.1.4 贝叶斯分类器
(1)朴素贝叶斯分类器
(2)半朴素贝叶斯分类器
(3)贝叶斯网
3.1.5 神经网络
常见的神经网络有:
(1)RBF网络
(2)ART网络
(3)SOM网络
(4)级联相关网络
(5)Elman网络
(6)Boltzman机
(7)深度学习
3.1.6支持向量机
3.2聚类
3.2.1划分聚类
3.2.2继承聚类
3.2.3密度聚类
3.2.4 基于图的聚类
3.2.5可伸缩聚类算法
3.3关联分析
3.3.1 Apriori算法
3.3.2 FP-growth算法
3.4 异常检测
四、数据后处理
在分析完数据后,通常需要使用合适的后处理方法对数据的结果进行显示,其实在数据挖掘里面主要称作可视化数据挖掘。(注意:这里虽然将数据可视化放在数据后处理小结里面,但是实际操作中,数据可视化通常也在数据预处理中使用,目的是为了找到数据之间的关系,来决定后面使用什么方法进行进一步分析。)
4.1 数据可视化
数据可视化,是关于数据视觉表现形式的科学技术研究。其中,这种数据的视觉表现形式被定义为,一种以某种概要形式抽提出来的信息,包括相应信息单位的各种属性和变量。
4.1.1 少量数据可视化
(1)茎叶图
它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少。
(2)直方图
直方图(Histogram)又称质量分布图。是一种统计报告图,由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类型,纵轴表示分布情况。直方图是数值数据分布的精确图形表示。
(4)盒状图
它由五个数值点组成:最小值(min),下四分位数(Q1),中位数(median),上四分位数(Q3),最大值(max)。也可以往盒图里面加入平均值(mean)。下四分位数、中位数、上四分位数组成一个“带有隔间的盒子”。上四分位数到最大值之间建立一条延伸线,这个延伸线成为“胡须(whisker)”。
(5)饼图
(6)百分位数图
可表示为:一组n个观测值按数值大小排列。如,处于p%位置的值称第p百分位数。
(7)散布图
制作散布图的目的是为辨认一个品质特征和一个可能原因因素之间的联系。
4.1.2 可视化时间空间数据
(1)等高线图
(2)曲面图
排列在工作表的列或行中的数据可以绘制到曲面图中。如果您要找到两组数据之间的最佳组合,可以使用曲面图。就像在地形图中一样,颜色和图案表示具有相同数值范围的区域。
(3)矢量场图
在某些数据中,一个特性可能同时具有值和方向。在这种情况下,同时显示方向和量的图可能是有用的。
4.1.3 可视化高维数据
(1)矩阵
图像可以看作像素的矩阵阵列,其中每个像素用它的颜色和亮度刻画,数据矩阵是值的矩形阵列。
(2)平行坐标系