【BZOJ2154】Crash的数字表格（莫比乌斯反演）

题意：

 

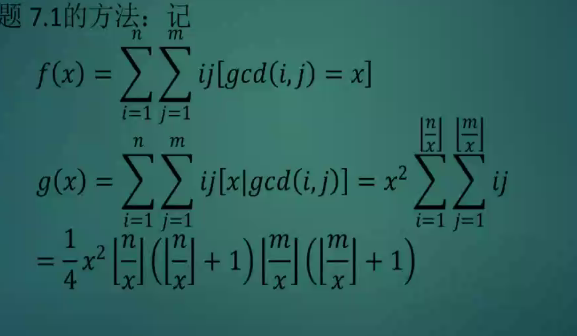
思路：如上

From http://blog.csdn.net/regina8023/article/details/44243911

最后的F(x,y)的推法和求gcd(x,y)=1的(x,y)对数差不多，只不过在推导过程中把原来1的地方换成x*y。

那么我们预处理出i^2*u[i]的前缀和，F(x,y)可以在O(sqrt(n))时间内求出来，而ans的式子也可以在O(sqrt(n))中求出来，

因此最后的时间复杂度是O(n)的。

const mo=20101009;
var flag,prime,mu:array[0..10000000]of longint;
    sum:array[0..10000000]of int64;
    n1,m1,i,j,max,m,t,x,y,t1,t2:longint;
    ans,pos:int64;

function ask(n,m:int64):int64;
begin
 n:=n*(n+1) div 2 mod mo;
 m:=m*(m+1) div 2 mod mo;
 exit(n*m mod mo);
end;

function clac(n,m:longint):int64;
var t1,t2,i,pos:longint;
    x,y:int64;
begin
 i:=1; clac:=0;
 while i<=n do
 begin
  x:=n div i; y:=m div i;
  t1:=n div x; t2:=m div y;
  if t1<t2 then pos:=t1
   else pos:=t2;
  clac:=clac+ask(x,y)*(sum[pos]-sum[i-1]) mod mo;
  clac:=(clac mod mo+mo) mod mo;
  i:=pos+1;
 end;
end;

begin
 assign(input,'bzoj2154.in'); reset(input);
 assign(output,'bzoj2154.out'); rewrite(output);
 readln(n1,m1);
 if n1>m1 then max:=n1
  else max:=m1;
 mu[1]:=1;
 for i:=2 to max do
 begin
  if flag[i]=0 then
  begin
   inc(m); prime[m]:=i;
   mu[i]:=-1;
  end;
  j:=1;
  while (j<=m)and(prime[j]*i<=max) do
  begin
   t:=prime[j]*i; flag[t]:=1;
   if i mod prime[j]=0 then
   begin
    mu[t]:=0;
    break;
   end;
   mu[t]:=-mu[i];
   inc(j);
  end;
 end;
 for i:=1 to max do sum[i]:=(sum[i-1]+int64(mu[i])*i*i) mod mo;
 if n1>m1 then
 begin
  t:=n1; n1:=m1; m1:=t;
 end;
 i:=1;
 while i<=n1 do
 begin
  x:=n1 div i; y:=m1 div i;
  t1:=n1 div x; t2:=m1 div y;
  if t1<t2 then pos:=t1
   else pos:=t2;
  ans:=ans+(pos-i+1)*(pos+i) div 2 mod mo*clac(x,y) mod mo;
  ans:=ans mod mo;
  i:=pos+1;
 end;
 writeln(ans);
 close(input);
 close(output);
end.

 UPD（2018.10.22）：C++

#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<vector>
using namespace std;
typedef long long ll;
typedef unsigned int uint;
typedef unsigned long long ull;
typedef pair<int,int> PII;
typedef vector<int> VI;
#define fi first
#define se second
#define MP make_pair
#define MAXN 10000000 
#define eps 1e-8
#define pi  acos(-1)
#define oo  1e9
#define MOD 20101009
 
int flag[MAXN+10],prime[MAXN+10],mu[MAXN+10];
ll s[MAXN+10];
 
ll ask(ll n,ll m)
{
    n=n*(n+1)/2%MOD;
    m=m*(m+1)/2%MOD;
    return n*m%MOD;
}
 
ll calc(int n,int m)
{
    int i=1; 
    ll ans=0;
    while(i<=n)
    {
        ll x=n/i; ll y=m/i;
        ll t1=n/x; ll t2=m/y;
        ll pos=min(t1,t2);
        ans+=ask(x,y)*(s[pos]-s[i-1])%MOD;
        ans=(ans%MOD+MOD)%MOD;
        i=pos+1;
    }
    return ans;
}
 
int main()
{
    int N,M;
    scanf("%d%d",&N,&M);
    int MAX=max(N,M);
    mu[1]=1;
    int m=0;
    for(int i=2;i<=MAX;i++)
    {
        if(!flag[i])
        {
            prime[++m]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=m;j++)
        {
            int t=prime[j]*i;
            if(t>MAX) break; 
            flag[t]=1;
            if(i%prime[j]==0)
            {
                mu[t]=0;
                break;
            }
            mu[t]=-mu[i];
        }
    }
     
    for(int i=1;i<=MAX;i++) s[i]=(s[i-1]+1ll*mu[i]*i*i)%MOD;
    if(N>M) swap(N,M);
    int i=1;
    ll ans=0;
    while(i<=N)
    {
        int x=N/i; int y=M/i;
        int t1=N/x; int t2=M/y;
        ll pos=min(t1,t2);
        ans+=(pos-i+1)*(pos+i)/2*calc(x,y)%MOD;
        ans%=MOD;
        i=pos+1;
    }
    printf("%lld
",ans); 
    return 0;
}