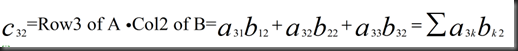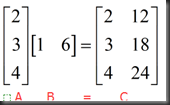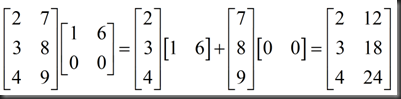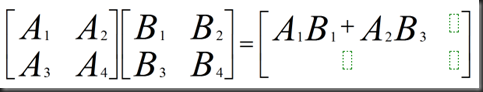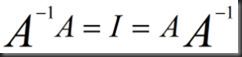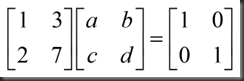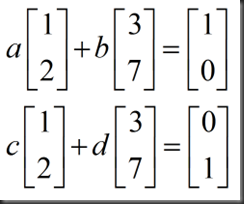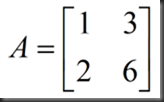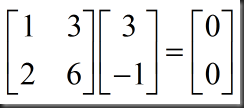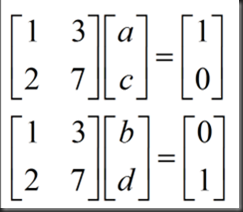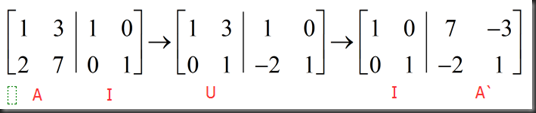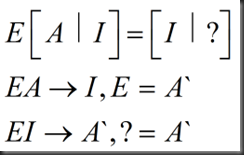Matrix multiplication(4 ways!)
Inverse of A
Gauss-Jordan / find inverse of A
Matrix multiplication
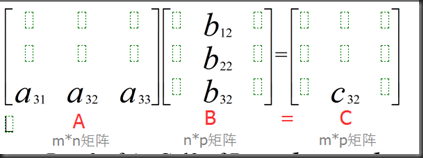
1、点积法
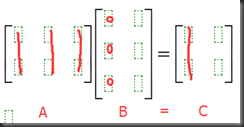
2、matrix * column=comb of columns
columns of C are comb of cols of A
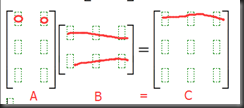
3、matrix * row = comb of rows
rows of C are comb of rows of B
4、matrix * matrix=comb of row*col
AB=sum of (cols of A )*(rows of B)
another example:
*5、Block (分块行 * 分块列)
Inverses( Square matrices)
if inverse of A exits, then
invertible, non-singular
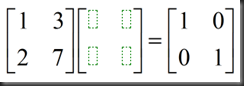
思考如何求此矩阵的逆,矩阵及其逆应满足条件:
设逆矩阵由元素a,b,c,d构成,如图:
以上讨论的都是逆矩阵存在的情况,下面举例讨论逆矩阵不存在的情况(singular case,no inverse),
可以从以下三方面来解释:
1、行列式为0
2、假设A`存在,A中两列向量共线,所以不可能通过线性组合构成单位矩阵,AA`≠I,就没有A`的说法了
3、You can find a vector X with AX=0 (X≠0)
由于AX=0,假设A`存在,等式两边同时乘以A`,A`AX=A`0=0, IX=0,X=0 与 X≠0矛盾,故假设不成立
若矩阵中其中一列对线性组合毫无贡献,则矩阵不可能有逆
Gauss Jordan(solve 2 equations at once)
可得到A的逆矩阵形式为:
解释推导: