基于数组的完全二叉树

以下实现的是一个基于数组存储的完全二叉树

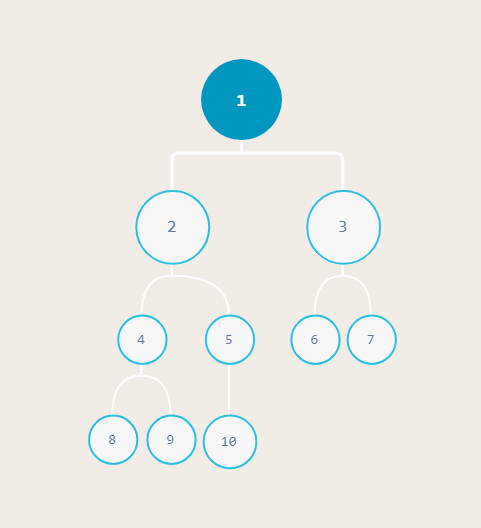
完全二叉树特征：

• 层序存储位置（k, p）与数组位置（i）之间的关系：i = 2^(p-1) + (q -1)
• 数组中，结点（p）与左子树（i）的位置关系：i = 2*p + 1
• 数组中，结点（p）与右子树（i）的位置关系：i = 2*p + 2
• 数组中，子结点（p）与父亲结点（i）的位置关系：i = (p + 1) / 2 - 1
• 深度 k 与 结点数 n 之间的关系： n <= (2^k - 1)

// BinaryTree
// BinaryTree
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

// 定义两个常量
#define MAXSIZE 100								// 存储空间初始分配量
#define MAX_TREE_SIZE 100						// 二叉树最大结点数
#define TRUE 1
#define FALSE 0
#define STATUS_OK 1
#define STATUS_FAILED 0

typedef int TElemType;
typedef TElemType BinaryTree[MAX_TREE_SIZE];		

// 定义二叉树的数据结构
typedef struct
{
	int level; // 结点的层
	int order; // 本层序号
}Position;

TElemType Nil = 0; // 定义TElemType的空类型

// 构造空二叉树
void InitBiTree(BinaryTree T)
{
	for (int i = 0; i < MAX_TREE_SIZE; i++)
	{
		T[i] = Nil;
	}
}
#define ClearBiTree InitBiTree // 在顺序存储结构中，两函数完全一样

int BiTreeEmpty(BinaryTree T)
{
	if (T[0] == Nil)
	{
		return TRUE;
	}
	else
	{
		return FALSE;
	}
}

void visit(TElemType e)
{
	printf(" %d ", e);
}

int Root(BinaryTree T, TElemType* e)
{
	if (!BiTreeEmpty(T)) { // 不空，e赋值根结点
		*e = T[0];
		return STATUS_OK;
	} else { // 空，返回错误状态
		return STATUS_FAILED;
	}
}

// 深度计算
// 利用了性质：深度为k的二叉树的结点数: n <= (2^k - 1)
int BiTreeDepth(BinaryTree T)					
{
	int i, j = -1;
	for (i = MAX_TREE_SIZE - 1; i >= 0; i--)	// 找到最后一个结点
	{
		if (T[i] != Nil)						// 不为Nil的结点	
			break;
	}
	i++; // 结点数n + 1;
	do {
		j++;
	} while (i >= powl(2, j));					// 计算2的j次幂
	printf("计算深度时，对比i(n+1):%d, j(2^k):%d
", i, j);
	return j;
}

// 以层序创建基于数组的完全二叉树（10个结点）, 此时双亲结点i与左右子树的索引关系：2*i+1, 2*1+2
void CreateBiTree(BinaryTree T)
{
	int i = 0;
	printf("请按层序输入结点的值(整型)，0表示空结点，输999结束。结点数≤%d:
", MAX_TREE_SIZE);
	while (i < 10)								// 层序遍历创建一个10个结点的二叉树
	{
		T[i] = i + 1;							// T[0] - T[9]: 1 2 3 4 5 6 7 8 9 10
		if (i != 0 && T[(i + 1) / 2 - 1] == Nil 
			&& T[i] != Nil)						// 此结点(不空)无双亲且不是根【目前没见过此种情况的出现】
		{
			printf("出现无双亲的非根结点%d
", T[i]);
			exit(0);
		}
		i++;
	}
	while (i < MAX_TREE_SIZE)
	{
		T[i] = Nil;
		i++;
	}
}

void TraverseArray(BinaryTree T)
{
	for (int i = MAX_TREE_SIZE - 1; i >= 0; i--)
	{
		visit(T[i]);
	}
}

void LevelOrderTraverse(BinaryTree T) 
{
	int i = MAX_TREE_SIZE - 1, j;
	while (T[i] == Nil)
	{
		i--;									// 找到最后一个非空结点的序号
	}
		
	for (j = 0; j <= i; j++)					// 从根结点起,按层序遍历二叉树
	{
		if (T[j] != Nil)
			visit(T[j]);						// 只遍历非空的结点
	}
	printf("
");
}

void PreTraverse(BinaryTree T, int index)
{
	visit(T[index]);							// 访问根结点
	if (T[2 * index + 1] != Nil)				// 左子树不空
		PreTraverse(T, 2 * index + 1);
	if (T[2 * index + 2] != Nil)				// 右子树不空 
		PreTraverse(T, 2 * index + 2);
}

void PreOrderTraverse(BinaryTree T)
{
	if (!BiTreeEmpty(T)) /* 树不空 */
		PreTraverse(T, 0);
	printf("
");
}

void InTraverse(BinaryTree T, int index)
{
	if (T[2 * index + 1] != Nil) /* 左子树不空 */
		InTraverse(T, 2 * index + 1);
	visit(T[index]);
	if (T[2 * index + 2] != Nil) /* 右子树不空 */
		InTraverse(T, 2 * index + 2);
}

void InOrderTraverse(BinaryTree T)
{
	if (!BiTreeEmpty(T)) /* 树不空 */
		InTraverse(T, 0);
	printf("
");
}

void PostTraverse(BinaryTree T, int index)
{
	if (T[2 * index + 1] != Nil) /* 左子树不空 */
		PostTraverse(T, 2 * index + 1);
	if (T[2 * index + 2] != Nil) /* 右子树不空 */
		PostTraverse(T, 2 * index + 2);
	visit(T[index]);
}

void PostOrderTraverse(BinaryTree T)
{
	if (!BiTreeEmpty(T)) /* 树不空 */
		PostTraverse(T, 0);
	printf("
");
}
// [(2^(k-1)-1) + (q-1)]
int Value(BinaryTree T, Position p)
{
	return T[(int)powl(2, p.level - 1) + p.order - 2];
}

void Assign(BinaryTree T, Position p, TElemType value)
{
	int i = (int)powl(2, p.level - 1) + p.order - 2; // 将层号、本层序号转为矩阵的序号 
	if (value != Nil && T[(i + 1) / 2 - 1] == Nil) /* 给叶子赋非空值但双亲为空 */
		return;
	else if (value == Nil && (T[i * 2 + 1] != Nil || T[i * 2 + 2] != Nil)) /*  给双亲赋空值但有叶子（不空） */
		return;
	T[i] = value;
}

TElemType Parent(BinaryTree T, TElemType e)
{
	int i;
	if (T[0] == Nil) /* 空树 */
		return Nil;
	for (i = 1; i <= MAX_TREE_SIZE - 1; i++)
		if (T[i] == e) /* 找到e */
			return T[(i + 1) / 2 - 1];
	return Nil; /* 没找到e */
}

/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的左孩子。若e无左孩子,则返回＂空＂ */
TElemType LeftChild(BinaryTree T, TElemType e)
{
	int i;
	if (T[0] == Nil) /* 空树 */
		return Nil;
	for (i = 0; i <= MAX_TREE_SIZE - 1; i++)
		if (T[i] == e) /* 找到e */
			return T[i * 2 + 1];
	return Nil; /* 没找到e */
}

/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的右孩子。若e无右孩子,则返回＂空＂ */
TElemType RightChild(BinaryTree T, TElemType e)
{
	int i;
	if (T[0] == Nil) /* 空树 */
		return Nil;
	for (i = 0; i <= MAX_TREE_SIZE - 1; i++)
		if (T[i] == e) /* 找到e */
			return T[i * 2 + 2];
	return Nil; /* 没找到e */
}

/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回＂空＂ */
TElemType LeftSibling(BinaryTree T, TElemType e)
{
	int i;
	if (T[0] == Nil) /* 空树 */
		return Nil;
	for (i = 1; i <= MAX_TREE_SIZE - 1; i++)
		if (T[i] == e && i % 2 == 0) /* 找到e且其序号为偶数(是右孩子) */
			return T[i - 1];
	return Nil; /* 没找到e */
}

/* 初始条件: 二叉树T存在,e是T中某个结点 */
/* 操作结果: 返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回＂空＂ */
TElemType RightSibling(BinaryTree T, TElemType e)
{
	int i;
	if (T[0] == Nil) /* 空树 */
		return Nil;
	for (i = 1; i <= MAX_TREE_SIZE - 1; i++)
		if (T[i] == e && i % 2) /* 找到e且其序号为奇数(是左孩子) */
			return T[i + 1];
	return Nil; /* 没找到e */
}

int main()
{
	Position p;
	TElemType e;
	BinaryTree T;
	int result;
	InitBiTree(T);
	CreateBiTree(T);
	printf("建立二叉树后,树空否？%d(1:是 0:否) 树的深度=%d
", BiTreeEmpty(T), BiTreeDepth(T));

	Root(T, &e);
	printf("二叉树的根为：%d
", e);
		
	printf("层序遍历二叉树:
");
	LevelOrderTraverse(T);
	printf("前序遍历二叉树:
");
	PreOrderTraverse(T);
	printf("中序遍历二叉树:
");
	InOrderTraverse(T);
	printf("后序遍历二叉树:
");
	PostOrderTraverse(T);

	printf("修改结点的层号3本层序号2。");
	p.level = 3;
	p.order = 2;
	e = Value(T, p);
	printf("待修改结点的原值为%d请输入新值:50 ", e);
	e = 50;
	Assign(T, p, e);

	printf("前序遍历二叉树:
");
	PreOrderTraverse(T);
	printf("结点%d的双亲为%d,", e, Parent(T, e));
	printf("左右孩子分别为%d,%d,", LeftChild(T, e), RightChild(T, e));
	printf("左右兄弟分别为%d,%d
", LeftSibling(T, e), RightSibling(T, e));


	ClearBiTree(T);
	printf("清除二叉树后,树空否？%d(1:是 0:否) 树的深度=%d
", BiTreeEmpty(T), BiTreeDepth(T));
	TraverseArray(T);
	result = Root(T, &e);
	if (result == STATUS_OK)
		printf("二叉树的根为：%d
", e);
	else
		printf("树空，无根
");
	
}