In Berland it is the holiday of equality. In honor of the holiday the king decided to equalize the welfare of all citizens in Berland by the expense of the state treasury.
Totally in Berland there are n citizens, the welfare of each of them is estimated as the integer in ai burles (burle is the currency in Berland).
You are the royal treasurer, which needs to count the minimum charges of the kingdom on the king's present. The king can only give money, he hasn't a power to take away them.
The first line contains the integer n (1 ≤ n ≤ 100) — the number of citizens in the kingdom.
The second line contains n integers a1, a2, ..., an, where ai (0 ≤ ai ≤ 106) — the welfare of the i-th citizen.
In the only line print the integer S — the minimum number of burles which are had to spend.
5
0 1 2 3 4
10
5
1 1 0 1 1
1
3
1 3 1
4
1
12
0
In the first example if we add to the first citizen 4 burles, to the second 3, to the third 2 and to the fourth 1, then the welfare of all citizens will equal 4.
In the second example it is enough to give one burle to the third citizen.
In the third example it is necessary to give two burles to the first and the third citizens to make the welfare of citizens equal 3.
In the fourth example it is possible to give nothing to everyone because all citizens have 12 burles.
题意:
没个数只能加不能减,要求n个数相同,求最小代价...
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;
const int maxn=100+5;
int n,ans,Max,a[maxn];
signed main(void){
scanf("%d",&n);Max=0;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),Max=max(Max,a[i]);
ans=0;
for(int i=1;i<=n;i++)
ans+=Max-a[i];
printf("%d
",ans);
return 0;
}//Cap ou pas cap. Pas cap.
Nothing is eternal in the world, Kostya understood it on the 7-th of January when he saw partially dead four-color garland.
Now he has a goal to replace dead light bulbs, however he doesn't know how many light bulbs for each color are required. It is guaranteed that for each of four colors at least one light is working.
It is known that the garland contains light bulbs of four colors: red, blue, yellow and green. The garland is made as follows: if you take any four consecutive light bulbs then there will not be light bulbs with the same color among them. For example, the garland can look like "RYBGRYBGRY", "YBGRYBGRYBG", "BGRYB", but can not look like "BGRYG", "YBGRYBYGR" or "BGYBGY". Letters denote colors: 'R' — red, 'B' — blue, 'Y' — yellow, 'G' — green.
Using the information that for each color at least one light bulb still works count the number of dead light bulbs of each four colors.
The first and the only line contains the string s (4 ≤ |s| ≤ 100), which describes the garland, the i-th symbol of which describes the color of the i-th light bulb in the order from the beginning of garland:
- 'R' — the light bulb is red,
- 'B' — the light bulb is blue,
- 'Y' — the light bulb is yellow,
- 'G' — the light bulb is green,
- '!' — the light bulb is dead.
The string s can not contain other symbols except those five which were described.
It is guaranteed that in the given string at least once there is each of four letters 'R', 'B', 'Y' and 'G'.
It is guaranteed that the string s is correct garland with some blown light bulbs, it means that for example the line "GRBY!!!B" can not be in the input data.
In the only line print four integers kr, kb, ky, kg — the number of dead light bulbs of red, blue, yellow and green colors accordingly.
RYBGRYBGR
0 0 0 0
!RGYB
0 1 0 0
!!!!YGRB
1 1 1 1
!GB!RG!Y!
2 1 1 0
In the first example there are no dead light bulbs.
In the second example it is obvious that one blue bulb is blown, because it could not be light bulbs of other colors on its place according to the statements.
题意:
给出一个字符串,合法的字符串只有四种字符:RYBG,并且任意四个连续的字符中没有重复字符,现在一些字符被替换成了!,求出原来的字符串中被替换成RYGB的分别有多少个(数据保证答案唯一)...
分析:
很显然如果把字符串以4为单位长度划分,每个单位是一样的...所以我们求出每个单位的子串的样子扫一遍计算就好...
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;
const int maxn=100+5;
int n,co[5],cnt[5];
char s[maxn];
inline int mp(char l){
if(l=='R')
return 1;
if(l=='B')
return 2;
if(l=='Y')
return 3;
if(l=='G')
return 4;
}
signed main(void){
scanf("%s",s+1);n=strlen(s+1);
int i=1;
while(i<=n){
if(s[i]!='!')
co[1]=mp(s[i]),i=n+1;
i+=4;
}
i=2;
while(i<=n){
if(s[i]!='!')
co[2]=mp(s[i]),i=n+1;
i+=4;
}
i=3;
while(i<=n){
if(s[i]!='!')
co[3]=mp(s[i]),i=n+1;
i+=4;
}
i=4;
while(i<=n){
if(s[i]!='!')
co[4]=mp(s[i]),i=n+1;
i+=4;
}
for(int i=1;i<=n;i++)
if(s[i]=='!')
cnt[co[(i-1)%4+1]]++;
printf("%d %d %d %d
",cnt[1],cnt[2],cnt[3],cnt[4]);
return 0;
}//Cap ou pas cap. Cap.
On the Literature lesson Sergei noticed an awful injustice, it seems that some students are asked more often than others.
Seating in the class looks like a rectangle, where n rows with m pupils in each.
The teacher asks pupils in the following order: at first, she asks all pupils from the first row in the order of their seating, then she continues to ask pupils from the next row. If the teacher asked the last row, then the direction of the poll changes, it means that she asks the previous row. The order of asking the rows looks as follows: the 1-st row, the 2-nd row, ..., the n - 1-st row, the n-th row, the n - 1-st row, ..., the 2-nd row, the 1-st row, the 2-nd row, ...
The order of asking of pupils on the same row is always the same: the 1-st pupil, the 2-nd pupil, ..., the m-th pupil.
During the lesson the teacher managed to ask exactly k questions from pupils in order described above. Sergei seats on the x-th row, on the y-th place in the row. Sergei decided to prove to the teacher that pupils are asked irregularly, help him count three values:
- the maximum number of questions a particular pupil is asked,
- the minimum number of questions a particular pupil is asked,
- how many times the teacher asked Sergei.
If there is only one row in the class, then the teacher always asks children from this row.
The first and the only line contains five integers n, m, k, x and y (1 ≤ n, m ≤ 100, 1 ≤ k ≤ 1018, 1 ≤ x ≤ n, 1 ≤ y ≤ m).
Print three integers:
- the maximum number of questions a particular pupil is asked,
- the minimum number of questions a particular pupil is asked,
- how many times the teacher asked Sergei.
1 3 8 1 1
3 2 3
4 2 9 4 2
2 1 1
5 5 25 4 3
1 1 1
100 100 1000000000000000000 100 100
101010101010101 50505050505051 50505050505051
The order of asking pupils in the first test:
- the pupil from the first row who seats at the first table, it means it is Sergei;
- the pupil from the first row who seats at the second table;
- the pupil from the first row who seats at the third table;
- the pupil from the first row who seats at the first table, it means it is Sergei;
- the pupil from the first row who seats at the second table;
- the pupil from the first row who seats at the third table;
- the pupil from the first row who seats at the first table, it means it is Sergei;
- the pupil from the first row who seats at the second table;
The order of asking pupils in the second test:
- the pupil from the first row who seats at the first table;
- the pupil from the first row who seats at the second table;
- the pupil from the second row who seats at the first table;
- the pupil from the second row who seats at the second table;
- the pupil from the third row who seats at the first table;
- the pupil from the third row who seats at the second table;
- the pupil from the fourth row who seats at the first table;
- the pupil from the fourth row who seats at the second table, it means it is Sergei;
- the pupil from the third row who seats at the first table;
题意:
老师点名,按顺序点:第一行,第二行...第n-1行,第n行,第n-1行......,每一行都从第一列点到最后一列,求被点到次数最多的人的次数。最少的次数,以及(x,y)被点到的次数...
分析:
思路很简单,就是写起来需要考虑周全,细节要考虑全面...
我们把先抛去前n*m次点名,然后以后每(n-1)*2行为一组:(蓝色的区域,灰色为点名顺序)

每一组第一行和最后一行都只被点了一次,中间的被点了两次,所以最多的和最少的就可以算出来了,然后出去整组的,不全的分类讨论一下就好...
n=1的时候要特判...
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
#define int long long
using namespace std;
int n,m,x,y,k,ans1,ans2,ans3;
signed main(void){ans1=ans2=ans3=0;
scanf("%I64d%I64d%I64d%I64d%I64d",&n,&m,&k,&x,&y);
if(n==1){
ans1=ans2=ans3=k/m;
k=k%m;
if(k){
ans1++;
if(y<=k)
ans2++;
}
}
else if(n==2){
ans1=ans2=ans3=k/(2*m);
k=k%(2*m);
if(k>0&&k<2*m){
ans1++;
if(k>=(x-1)*m+y)
ans2++;
}
else if(k==2*m){
ans1++,ans2++,ans3++;
}
else if(k>0){
ans1+=2,ans3++,ans2++;k-=2*m;
if(k>=(x-1)*m+y)
ans2++;
}
}
else{
if(k<=n*m){
if(k<n*m)
ans3=0;
else
ans3=1;
ans1=1;
if(k>=(x-1)*m+y)
ans2=1;
else
ans2=0;
}
else{ans1=ans2=ans3=1;
k-=n*m;int lala=(n*2-2)*m;
ans1+=k/lala*2,ans3+=k/lala;
if(x!=1&&x!=n)
ans2+=k/lala*2;
else
ans2+=k/lala;
k=k%lala;
if(k&&k<=(n-1)*m){
ans1++;
if(x!=n&&k>=(n-1-x)*m+y)
ans2++;
}
else if(k){
ans1+=2;
if(x==n){
if(k-(n*2-3)*m>=y)
ans2++;
}
else if(x==1){
ans2++;
}
else{
ans2++;
k-=(n-1)*m;
if(k>=(x-2)*m+y)
ans2++;
}
}
}
}
printf("%I64d %I64d %I64d",ans1,ans3,ans2);puts("");
return 0;
}//Cap ou pas cap. Pas cap.
Alexander is learning how to convert numbers from the decimal system to any other, however, he doesn't know English letters, so he writes any number only as a decimal number, it means that instead of the letter A he will write the number 10. Thus, by converting the number 475 from decimal to hexadecimal system, he gets 11311 (475 = 1·162 + 13·161 + 11·160). Alexander lived calmly until he tried to convert the number back to the decimal number system.
Alexander remembers that he worked with little numbers so he asks to find the minimum decimal number so that by converting it to the system with the base n he will get the number k.
The first line contains the integer n (2 ≤ n ≤ 109). The second line contains the integer k (0 ≤ k < 1060), it is guaranteed that the number k contains no more than 60 symbols. All digits in the second line are strictly less than n.
Alexander guarantees that the answer exists and does not exceed 1018.
The number k doesn't contain leading zeros.
Print the number x (0 ≤ x ≤ 1018) — the answer to the problem.
13
12
12
16
11311
475
20
999
3789
17
2016
594
In the first example 12 could be obtained by converting two numbers to the system with base 13: 12 = 12·130 or 15 = 1·131 + 2·130.
题意:
给出n,k,k是n进制下的一个数,把k转化成十进制,要求转化成的数最小...
分析:
还是细节题,思路依旧很简单...
贪心的分段,因为要求十进制数尽可能小,所以每一段的数都尽可能接近n...需要注意的是遇到0的时候...具体实现见代码...
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
#define int long long
using namespace std;
const int maxn=60+5;
int n,ans,len;
char str[maxn];
inline int power(int x,int y){
int res=1;
while(y){
if(y&1)
res*=x;
x*=x,y>>=1;
}
return res;
}
signed main(void){
scanf("%I64d%s",&n,str);
ans=0;len=strlen(str);int lala=0,bit=1;
if(len==1&&str[0]=='0'){
puts("0");return 0;
}
for(int i=len-1,po=1;i>=0;i--){
if(str[i]=='0'){
int tmp=i;
while(str[tmp]=='0')
tmp--;
int j=tmp+1,ttmp=str[tmp]-'0';
while(j<=i&&ttmp*10<n)
ttmp*=10,j++;
j--;
if(j==i&&ttmp*po+lala<n)
lala+=ttmp*po,po*=power(10,i-tmp+1),i=tmp;
else{
ans+=lala*bit,lala=ttmp,po=power(10,j-tmp+1);
if(i==len-1)
bit*=power(n,i-j);
else
bit*=power(n,i-j+1);
i=tmp;
}
}
else{
if((str[i]-'0')*po+lala>=n)
ans+=lala*bit,lala=str[i]-'0',bit*=n,po=10;
else
lala+=(str[i]-'0')*po,po*=10;
}
}
ans+=lala*bit;
printf("%I64d
",ans);
return 0;
}//Cap ou pas cap. Pas cap.
For given n, l and r find the number of distinct geometrical progression, each of which contains n distinct integers not less than l and not greater than r. In other words, for each progression the following must hold: l ≤ ai ≤ r and ai ≠ aj , where a1, a2, ..., an is the geometrical progression, 1 ≤ i, j ≤ n and i ≠ j.
Geometrical progression is a sequence of numbers a1, a2, ..., an where each term after first is found by multiplying the previous one by a fixed non-zero number d called the common ratio. Note that in our task d may be non-integer. For example in progression 4, 6, 9, common ratio is 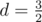 .
.
Two progressions a1, a2, ..., an and b1, b2, ..., bn are considered different, if there is such i (1 ≤ i ≤ n) that ai ≠ bi.
The first and the only line cotains three integers n, l and r (1 ≤ n ≤ 107, 1 ≤ l ≤ r ≤ 107).
Print the integer K — is the answer to the problem.
1 1 10
10
2 6 9
12
3 1 10
8
3 3 10
2
These are possible progressions for the first test of examples:
- 1;
- 2;
- 3;
- 4;
- 5;
- 6;
- 7;
- 8;
- 9;
- 10.
These are possible progressions for the second test of examples:
- 6, 7;
- 6, 8;
- 6, 9;
- 7, 6;
- 7, 8;
- 7, 9;
- 8, 6;
- 8, 7;
- 8, 9;
- 9, 6;
- 9, 7;
- 9, 8.
These are possible progressions for the third test of examples:
- 1, 2, 4;
- 1, 3, 9;
- 2, 4, 8;
- 4, 2, 1;
- 4, 6, 9;
- 8, 4, 2;
- 9, 3, 1;
- 9, 6, 4.
These are possible progressions for the fourth test of examples:
- 4, 6, 9;
- 9, 6, 4.
题意:
求长度为n的每一项都在区间[l,r]内的等比数列个数...(比值可以不是整数)...
分析:
我们可以只算比值大于1的数列个数,然后×2输出就是答案...
对于特殊情况n=1n=2的时候特判...n>30的时候一定是0...
然后其他的一般情况我们枚举分子分母互质的分数...计算答案...
定义x为分子,y为分母,那么 ,令
,令 ,那么a1=b*yn-1,an=b*xn-1,所以l<=a1<an<=r...
,那么a1=b*yn-1,an=b*xn-1,所以l<=a1<an<=r...
可以得出b的个数为  +1...
+1...
代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;
int n,l,r;
long long ans;
inline long long power(long long x,int y){
long long res=1;
while(y){
if(y&1)
res*=x;
x*=x,y>>=1;
}
return res;
}
inline int gcd(int x,int y){
return y==0?x:gcd(y,x%y);
}
signed main(void){
scanf("%d%d%d",&n,&l,&r);
int len=r-l+1;ans=0;
if(n==1){
printf("%d
",len);return 0;
}
else if(n==2){
printf("%I64d
",1LL*len*(len-1));return 0;
}
else if(n>30){
puts("0");return 0;
}
for(int i=1;;i++){
long long tmp=power(i*1LL,n-1);
if(tmp>r)
break;
for(int j=i+1;;j++){
long long ttmp=power(j,n-1);
if(ttmp>r)
break;
if(gcd(i,j)>1)
continue;
long long Min=(l+tmp-1)/tmp,Max=r/ttmp;
ans+=max(0LL,Max-Min+1);
}
}
printf("%I64d
",ans<<1);
return 0;
}//Cap ou pas cap. Cap.
未完待续...
By NeighThorn