SPOJ 1182 Sorted bit sequence

题目链接

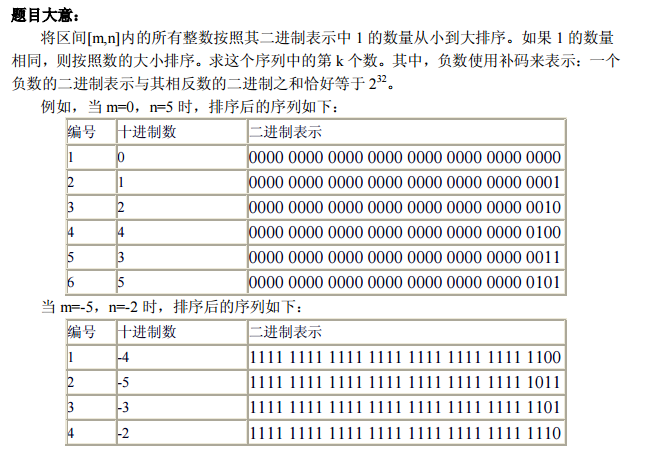
题意：

分析：

其实如果会了Ural 1057. Amount of Degrees那道题目，这道题自然也就会了...

我们考虑枚举第$k$个数字的$1$的个数，那么我们需要计算的也就是区间内二进制状态下$1$的个数为$x$的数字个数，这个的求法在上一题中写过了...

我们求到第$k$的数字的$1$的个数为$x$，那么我们去二分这个数字是什么，也就是说我们要求一个最靠左的右端点，使得区间$[n,ans]$内$1$的个数为$x$的数字个数恰好为$k$，然后总体思路就解决了...

细节方面就是要注意特判$0$，然后对于负数的处理就是先去掉负数的符号位，然后判断，最后输出的时候再把符号位加上...

具体实现看代码...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;

const int maxn=32+5;

int n,m,k,ans,cas,f[maxn][maxn];

inline void init(void){
	f[0][0]=1;
	for(int i=1;i<=31;i++){
		f[i][0]=1;
		for(int j=1;j<=i;j++)
			f[i][j]=f[i-1][j]+f[i-1][j-1];
	}
}

inline int calc(int x,int y){
	int cnt=0,ans=0;
	for(int i=31;i>=1;i--){
		if((x>>i)&1){
			cnt++;
			if(cnt>y) break;
			x=x^(1<<i);
		}
		if((1<<(i-1))<=x)
			ans+=f[i-1][y-cnt];
	}
	if(cnt+x==y) ans++;
	return ans;
}

inline int solve(void){
	int len=0;
	for(int i=0,tmp;i<=31;i++){
		tmp=calc(m,i)-calc(n-1,i);
		if(tmp>=k) break;
		k-=tmp;len=i+1;
	}
	long long l=n,r=m,ans;
	while(l<=r){
		long long mid=(l+r)>>1;
		if(calc(mid,len)-calc(n-1,len)>=k)
			ans=mid,r=mid-1;
		else
			l=mid+1;
	}
	return ans;
}

signed main(void){
#ifndef ONLINE_JUDGE
	freopen("in.txt","r",stdin);
#endif
	scanf("%d",&cas);init();
	while(cas--){
		scanf("%d%d%d",&n,&m,&k);
		if(m==0&&n==0){
			puts("0");
			continue;
		}
		int flag=0;
		if(n==0) n++,k--;
		if(m==0) m--,k--;
		if(n<0) n^=(1<<31),flag=1;
		if(m<0) m^=(1<<31),flag=1;
		ans=solve();
		if(flag) printf("%d
",(ans^(1<<31)));
		else printf("%d
",ans);
	}
	return 0;
}

　　

---

By NeighThorn