653. 两数之和 IV - 输入 BST
给定一个二叉搜索树 root 和一个目标结果 k,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
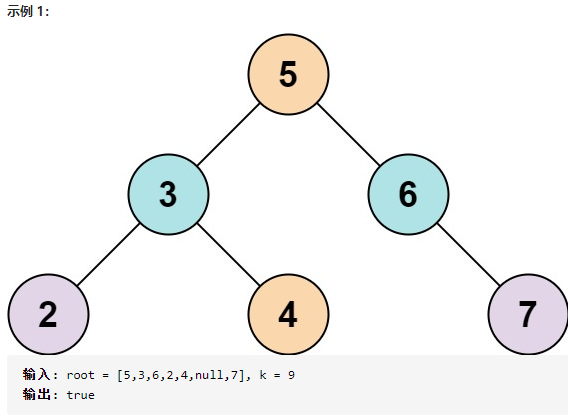

- 二叉树的节点个数的范围是
[1, 104]. -104 <= Node.val <= 104root为二叉搜索树-105 <= k <= 105
方法一:使用HashSet
如果存在两个元素之和为 kk,即 x+y=kx+y=k,并且已知 xx 是树上一个节点的值,则只需判断树上是否存在一个值为 yy 的节点,使得 y=k-xy=k−x。基于这种思想,在树的每个节点上遍历它的两棵子树(左子树和右子树),寻找另外一个匹配的数。在遍历过程中,将每个节点的值都放到一个 setset 中。
对于每个值为 pp 的节点,在 setset 中检查是否存在 k-pk−p。如果存在,那么可以在该树上找到两个节点的和为 kk;否则,将 pp 放入到 setset 中。
如果遍历完整棵树都没有找到一对节点和为 kk,那么该树上不存在两个和为 kk 的节点。
作者:LeetCode
链接:https://leetcode-cn.com/problems/two-sum-iv-input-is-a-bst/solution/liang-shu-zhi-he-iv-by-leetcode/
来源:力扣(LeetCode)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean findTarget(TreeNode root, int k) {
Set<Integer> set = new HashSet();
return find(root,k, set);
}
public boolean find(TreeNode root, int k, Set<Integer> set){
if(root == null){
return false;
}
if(set.contains(k-root.val)){
return true;
}
set.add(root.val);
return find(root.right, k, set)||find(root.left, k, set);
}
}
方法二:使用 BFS 和 HashSet
本方法中,setset 的用途与 方法一 相同。但是本方法使用广度优先搜索遍历二叉树,这是一种非常常见的遍历方法。
使用广度优先搜索查找一对节点和为 kk 的过程如下。首先维护一个与 方法一 用途相同的 setset。将根节点加入 queuequeue,然后执行以下步骤:
从队列首部删除一个元素 pp。
检查 setset 中是否存在 k-pk−p。如果存在,返回 True。
否则,将 pp 加入 setset。然后将当前节点的左孩子和右孩子加入 queuequeue。
重复步骤一至三,直到 queuequeue 为空。
如果 queuequeue 为空,返回 False。
按照以上步骤,逐层遍历二叉树。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean findTarget(TreeNode root, int k) {
Set<Integer> set = new HashSet();
Queue<TreeNode> queue = new LinkedList();
queue.add(root);
while(!queue.isEmpty()){
if(queue.peek()!=null){
TreeNode node = queue.remove();
if(set.contains(k - node.val)){
return true;
}
set.add(node.val);
queue.add(node.left);
queue.add(node.right);
}else{
queue.remove();
}
}
return false;
}
}
方法三 使用 BST
在本方法中利用 BST 的性质,BST 的中序遍历结果是按升序排列的。因此,中序遍历给定的 BST,并将遍历结果存储到 listlist 中。
遍历完成后,使用两个指针 ll 和 rr 作为 listlist 的头部索引和尾部索引。然后执行以下操作:
检查 ll 和 rr 索引处两元素之和是否等于 kk。如果是,立即返回 True。
如果当前两元素之和小于 kk,则更新 ll 指向下一个元素。这是因为当我们需要增大两数之和时,应该增大较小数。
如果当前两元素之和大于 kk,则更新 rr 指向上一个元素。这是因为当我们需要减小两数之和时,应该减小较大数。
重复步骤一至三,直到左指针 ll 大于右指针 rr。
如果左指针 ll 到右指针 rr 的右边,则返回 False。
注意:在任何情况下,都不应该增大较大的数,也不应该减小较小的数。这是因为如果当前两数之和大于 kk,不应该首先增大 list[r]list[r] 的值。类似的,也不应该首先减小 list[l] 的值。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean findTarget(TreeNode root, int k) {
List<Integer> list = new ArrayList();
reTree(root, list);
int l = 0;
int r = list.size() - 1;
while(l < r){
int sum = list.get(l) + list.get(r);
if (sum < k){
l++;
}
if(sum > k){
r--;
}
if(sum == k){
return true;
}
}
return false;
}
public void reTree(TreeNode root,List<Integer> list){
if(root == null){
return;
}
reTree(root.left,list);
list.add(root.val);
reTree(root.right,list);
}
}