网络延迟时间
有 n 个网络节点,标记为 1 到 n。
给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
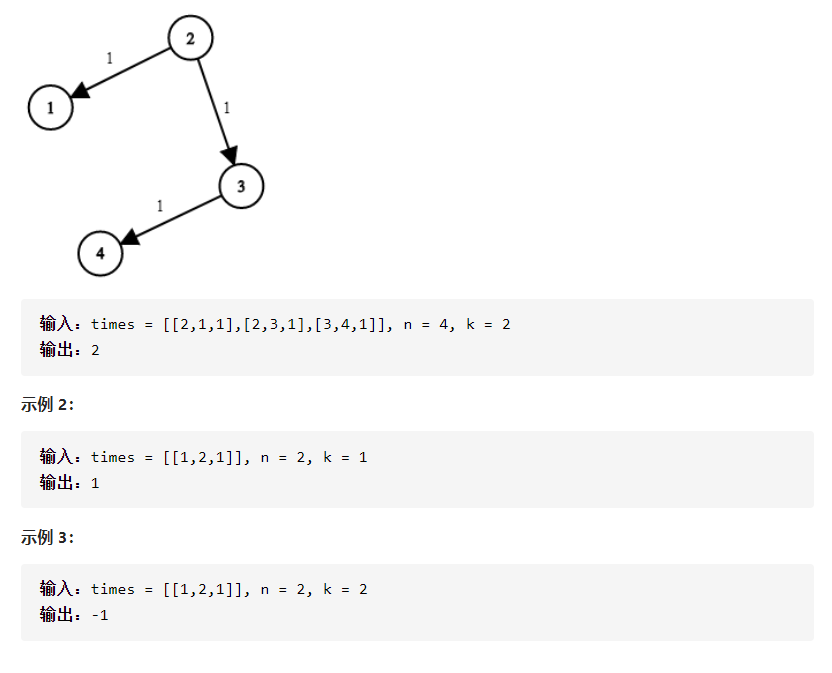
此题是个中等题,我用的dijkstra算法
具体代码和实现方法见此网址
【GTAlgorithm】图解算法,吃透一个Dijkstra就够了!C++/Java/Python - 网络延迟时间 - 力扣(LeetCode) (leetcode-cn.com)
从一个点出发,到所有点的最短距离或最短时间,换句话就是,求源点到所有点的最短距离的最大值
三种存图方式
1.邻接矩阵
当这是一种使用二维矩阵来进行存图的方式。适用于边数较多的稠密图使用,当边数量接近点的数量的平方,
时,可定义为稠密图。
// 邻接矩阵数组:w[a][b] = c 代表从 a 到 b 有权重为 c 的边
int[][] w = new int[N][N];
// 加边操作
void add(int a, int b, int c) {
w[a][b] = c;
}
2.邻接表
这也是一种在图论中十分常见的存图方式,与数组存储单链表的实现一致(头插法)。
这种存图方式又叫链式前向星存图。
适用于边数较少的稀疏图使用,当边数量接近点的数量,可定义为稀疏图。
int[] he = new int[N], e = new int[M], ne = new int[M], w = new int[M];
int idx;
void add(int a, int b, int c) {
e[idx] = b;
ne[idx] = he[a];
he[a] = idx;
w[idx] = c;
idx++;
}
。
3.类
这是一种最简单,但是相比上述两种存图方式,使用得较少的存图方式。
只有当我们需要确保某个操作复杂度严格为 O(m) 时,才会考虑使用。
具体的,我们建立一个类来记录有向边信息:
class Edge {
// 代表从 a 到 b 有一条权重为 c 的边
int a, b, c;
Edge(int _a, int _b, int _c) {
a = _a; b = _b; c = _c;
}
}
遍历
List<Edge> es = new ArrayList<>();
...
for (Edge e : es) {
...
}