人脸检测及识别python实现系列(4)——卷积神经网络(CNN)入门
上篇博文我们准备好了2000张训练数据,接下来的几节我们将详细讲述如何利用这些数据训练我们的识别模型。前面说过,原博文给出的训练程序使用的是keras库,对我的机器来说就是tensorflow版的keras。训练程序建立了一个包含4个卷积层的神经网络(CNN),程序利用这个网络训练我的人脸识别模型,并将最终训练结果保存到硬盘上。在我们实际动手操练之前我们必须先弄明白一个问题——什么是卷积神经网络(CNN)?
CNN(Convolutional Neural Network)——卷积神经网络,人工神经网络(Neural Network,NN)的一种,其它还有RNN、DNN等类型,而CNN就是利用卷积进行滤波的神经网络。换句话说,CNN就是卷积加神经网络。网上关于CNN的资料非常多,度娘一搜一大堆,良莠不齐,有不少资料过于艰深,对于刚入行的小白来说一上来看这种资料会迷失方向,产生极强的挫折感,有可能会让你失去学习的信心和兴趣。作为一个过来人,我对此深有体会。幸运的是,我还是找到了一些关于CNN讲得很不错的资料,首先是这个:
卷积神经网络详解 (1)
知乎上专栏作者张觉非的文章,讲得很不错,比较通俗。微信公众号“新智元”转发了此文,上面给出的链接就是转发地址,其原文链接为:https://zhuanlan.zhihu.com/p/25249694,不过原文链接有些图片显示不清楚,不知为何?如果你能够显示完整图片,建议直接看原文,转发文章与原文有些区别,并且代码不能直接粘贴。然后我们接着看这个:
一个简单的例子:离散卷积 (2)
其实,对于图像处理——离散卷积属于常用算法,这篇文章对利用卷积对图像滤波讲得比上一篇文章更浅显易懂,且只讲了这一点内容,很短,所以建议上篇文章看不下去的时候先转头看看这个再接着看上一篇,会有不错的效果。当然,对于喜欢追根究底的同学来说,仅看上面这两篇文章是远远不够的,可能你和我一样对于什么是卷积这个概念还不是很清楚,那么请接下来移步如下链接,看看他们对卷积的讨论和理解:
怎样通俗易懂的解释卷积 (3)
基本上这三篇文章就能基本了解CNN是怎么回事,能够看懂我在下一篇博文将要贴出的训练程序代码了。
首先,关于什么是卷积,文章(3)有一牛人用一句话总结得很好:卷积就是带权的积分,看下面的一维卷积公式:

函数值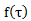 与权值
与权值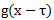 的乘积相加即可得到卷积值c(x),换句话说,我们对函数值
的乘积相加即可得到卷积值c(x),换句话说,我们对函数值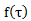 的加权叠加,即可得到x处的卷积值。CNN利用的是多维卷积,但原理一样,不多说了,同时建议不要过多纠缠这个概念,理解就好,以后若作科研再作深入了解。对于图像处理,CNN会对输入图像矩阵化,然后从矩阵第一个元素开始逐一进行卷积运算。在这里进行卷积运算的矩阵元素值即为
的加权叠加,即可得到x处的卷积值。CNN利用的是多维卷积,但原理一样,不多说了,同时建议不要过多纠缠这个概念,理解就好,以后若作科研再作深入了解。对于图像处理,CNN会对输入图像矩阵化,然后从矩阵第一个元素开始逐一进行卷积运算。在这里进行卷积运算的矩阵元素值即为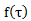 ,而
,而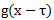 则被称为卷积核或者滤波器,需求不同我们选用的滤波器会有所不同,其卷积效果会不同。比如均值滤波器(average filter)会将图像模糊,而拉普拉斯滤波器(Laplacian filter)则会将图像局部细节增强。但假如我们既不想将图像模糊又不想将图像增强,而我们有其它古怪的需求呢?比如,我们正在做的人脸识别,如果输入的是我的脸部图像,经过CNN卷积处理后我想得到一个固定数值0来代表我;而输入我闺女的图像时,得到另一个数值1来代表她,这种需求我们该怎么办?这种情况下,我们就需要从一个随机滤波器开始,让CNN根据我们的需求利用某种算法调整滤波器使其逐渐接近目标,即能够根据输入图像的不同准确地输出0或者1这两个数值。那么CNN是怎么做到的呢?
则被称为卷积核或者滤波器,需求不同我们选用的滤波器会有所不同,其卷积效果会不同。比如均值滤波器(average filter)会将图像模糊,而拉普拉斯滤波器(Laplacian filter)则会将图像局部细节增强。但假如我们既不想将图像模糊又不想将图像增强,而我们有其它古怪的需求呢?比如,我们正在做的人脸识别,如果输入的是我的脸部图像,经过CNN卷积处理后我想得到一个固定数值0来代表我;而输入我闺女的图像时,得到另一个数值1来代表她,这种需求我们该怎么办?这种情况下,我们就需要从一个随机滤波器开始,让CNN根据我们的需求利用某种算法调整滤波器使其逐渐接近目标,即能够根据输入图像的不同准确地输出0或者1这两个数值。那么CNN是怎么做到的呢?
要想弄明白这个问题,我们必须先了解一下什么是人工神经网络(NN,Neural Network)?人工神经网络是一种计算模型,是由多层、每层多个人工神经元组成的复杂网络。单个人工神经元的结构见下图(该图来自百度图片,稍作修改):

其中,x1——xm为神经元的输入,w1-wm则是权值,b为偏置标量(可理解为线性方程的截距),我们对x1-xm逐一加权(w1-wm)求和后得到卷积值,卷积值与偏置值b相加得到c,我们再将c输出给“激活函数f(c)”,最终我们得到人工神经元的输出a,即:
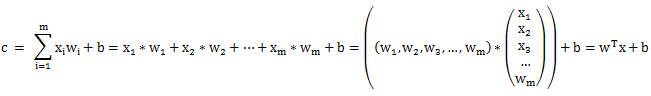
a = f(c)
需要特别交代的是:c = wTx+b为上述计算过程的向量表达形式,这样可以让公式看起来比较简洁(或者更高大上些)。其中w、x分别代表权值矩阵和输入数据矩阵,wT为w的转置矩阵。简单说就是我们将矩阵w的“行列”进行了转换,“列”变成了“行”后得到转置矩阵wT,这样即可实现w和x的逐个元素相乘叠加,其本质就是矩阵乘法。不懂的可以度娘查找矩阵乘法,很简单,就不多说了。
我们得到c值后,将其输入到激活函数进行处理,那么激活函数是干啥的呢?我的个人理解就是将简单的线性输入(上述加权叠加过程再复杂也是简单的线性组合)转换成复杂的非线性输出,以获得更好的分类效果。换句话说,我们需要利用激活函数将简单的线性分类变成复杂的非线性分类以获得更好的分类效果。举个例子,如下图:
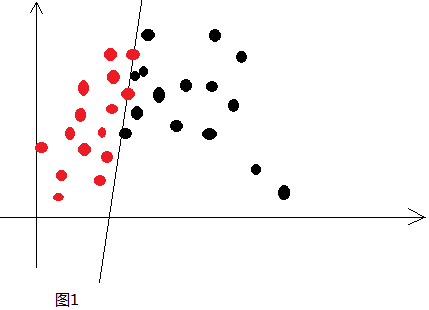
两种颜色代表两类数据,这两类数据很老实地呆在直线的两边,我们很容易找到准确描述这条直线的线性方程式,这就是简单的线性分类。但是,如果数据像下面这样呢:
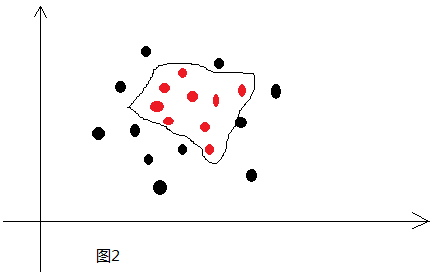
其实,绝大多数情况下,数据都应该是类似这样,而且比这还复杂。因为这仅仅是二维空间一个简单到能够一眼就能看出数据边界的例子,如果是三维、四维以及更高维的情况呢?一条简单的直线显然是办不到的。这种情况下只能用多层神经网络利用激活函数将简单的线性分类变成复杂的非线性分类,让分类边界变成复杂的曲线并且能够穿越多维空间,这样才能达成我们的目标,至于激活函数经过多层作用后,它到底会长什么样,谁也不知道,我们只是知道——It worked!常见的激活函数有sigmoid、tanh、ReLu、maxout等,以sigmoid函数为例,其函数式如下:
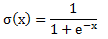
其具备类似阶跃函数的性质,其可以在跳跃点(某个数值)从0跳跃到1。该函数的值域为(0,1),人工神经元将sigmoid函数的输出与某个阀值进行比较,比如0.5,大于0.5,神经元输出1,小于则输出0。就这样我们把当前神经元的输出作为另一个神经元的输入,构成一个多层,每层多个神经元的复杂网络,如下图:
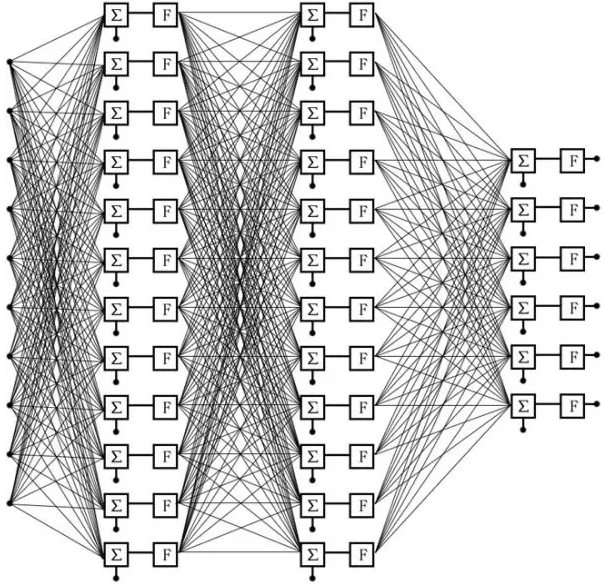
我直接将文章(1)的图截过来了,这个图很形象地展示了CNN的结构,其属于最简单的多层全连接前向神经网络系统,它有10个输入连接到了网络的第一层,每个输入均与第一层的所有神经元连接。第一层神经元的输出作为下一层神经元的输入连接到下一层,以此类推,直至最后一层神经元。上图共有三层网络,第1、2层各有12个神经元,第3层也就是最后一层有6个神经元,也就是说这个三层网络最后会有6个输出,即一个6元向量。
那么,类似这样的网络结构,是怎样理解并实现我们识别人脸这样的需求的呢?接下来就是训练数据登场的时候了。在这里,我们将训练数据称为训练集,每组训练数据包括一个输入、一个输出,也就是ML经常提到的带标注的数据,标注值为输出,图像等需要识别的内容为输入,N对这样的数据构成了训练数据集。以我们前面准备的人脸识别数据为例,我的1000张脸部图像作为输入数据,每输入一张图像,CNN的输出应为0,也就是说,一张图像对应一个固定数值0,1000张图像与1000个0组成1000对训练集。同样,闺女的1000张脸部图像与1000个1组成另外1000对训练集。我们首先将脸部图像作为输入数据输入给CNN,CNN从一个随机滤波器开始计算,其最终的输出基本不太可能是正确的,但这不要紧,CNN会将自己的输出Ocnn与数据集给出的输出Oreal进行比较,见下式:
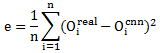
我们求得n对样本数据的真实值与输出值之间差的平方和的均值e,此处e被称作均方误差,亦即mse。显然e越小,其越接近真实输出,于是CNN的实际工作就变为想方设法地让e变小,直至e值进入可接受范围之内,此时我们就可以认为CNN训练好了。像e这样的函数我们统称为代价函数(Cost Function),除了mse,我们还可以选择其它代价函数用于调优。那么我们怎么才能调优呢?答案是使用梯度下降算法找到e的全局最小值,说白了就是求偏导。CNN会沿着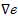 的相反方向调整权值和偏置值(顺着
的相反方向调整权值和偏置值(顺着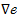 的方向e值上升最快,反之则下降最快,不了解的可参阅高等数学之偏导数及向量两部分内容,建议先看向量了解个大概再看偏导,更弱的就先看导数),一次一个步长(步长被称为学习效率,Learning Rate),如此反复,经过多次迭代,CNN即可得到e的最小值。于是,我们的目标达成。
的方向e值上升最快,反之则下降最快,不了解的可参阅高等数学之偏导数及向量两部分内容,建议先看向量了解个大概再看偏导,更弱的就先看导数),一次一个步长(步长被称为学习效率,Learning Rate),如此反复,经过多次迭代,CNN即可得到e的最小值。于是,我们的目标达成。
我相信你只要仔细阅读并真正理解了上面讲述的内容,那么接下来读懂训练代码应该不成问题了。如果你觉得还不过瘾,还想了解得更深,那么关于卷积神经网络更详细的内容,请详细阅读本文开头给出的几篇文章,或者看知乎上关于它的讨论帖,也很不错,唯一的小缺点是有点长。
最后,还需要交代一点:事实上,上面给出的三层卷积神经网络的结构图是非常简单的,仅仅包含三层单一的卷积层,我们接下来实际使用的CNN网络还需要几种特殊的网络层才能让CNN更加成熟,包括pooling layer、Dropout layer、flatten layer、dense layer等,下一节我将结合代码来详细讲解它们的实际用处,这里就不多说了。