GBDT Gradient Boosting Decision Tree
参考资料:
GBDT是什么?
GBDT是传统机器学习算法中对真实分布拟合最好的几种算法之一,在各大数据挖掘竞赛中常常出现前几名都采用GBDT算法,直到深度学习算法如潮水般涌来……。GBDT可以用于回归任务,也可以用于分类任务,还可以筛选特征。
GBDT的核心思想是采用基函数的线性组合,不断减小训练过程得出的残差来实现数据的分类和回归。具体来说,GBDT将经历多轮迭代,每次迭代生成一个弱分类器,而每个分类器在上一轮分类器的残差基础上进行训练。
弱分类器:复杂度不高,通常具有低方差和高偏差。
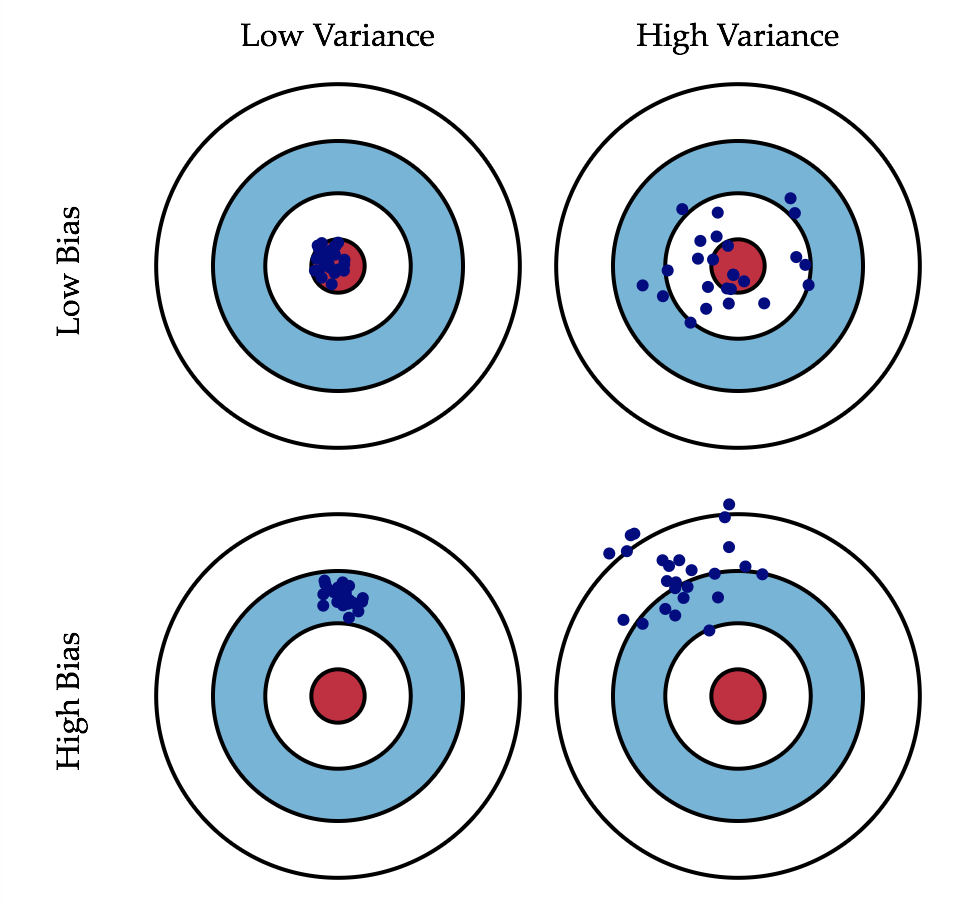
方差和偏差:偏差描述了分类器在训练数据上预测的准确度。方差描述了分类器中不同迭代情况下的预测精度变化程度。通常来说,模型越复杂,对训练数据的拟合程度越高,偏差越低,但是方差会越高。
GBDT的理论基础
当我们试图估计一个有参数模型\(F\)时,设\(F\)的参数集合为\(P\),那么我们将\(F\)视作一系列带参数的函数的线性组合:
其中\(a_m\in P\),\(\beta\)是权重参数。
通常来说,我们采用梯度下降方法来优化参数集合\(P\),即:
因此对应于第m次迭代,步长是\(\bold p_m\),因此\(P_{m}=\sum_{i=0}^{m}\bold p_i\),即对应第m次迭代的模型。从形式上看,我们用第m-1次迭代的模型的参数计算出第m次迭代时的梯度\(\bold g_m\),然后利用这个梯度得出新的步长\(\bold p_m\),由此计算出新的第m次迭代模型\(P_m\)
而对于一个无参数模型,我们将每个数据点\(\bold x_i\)处的函数值\(F(\bold x_i)\)看作这个函数的参数,我们用有限个离散点\(\{F(\bold x_i)\}_1^N\)来描述它们,因此上述梯度下降可以被描述为:
同样的,第m次迭代的模型\(F^*(\bold x)=\sum_{i=0}^Mf_i(x)\)
\(E_{y,\bold x}\)这种数学期望带下标的符号的含义,可参考这篇文章点我
而GBDT的每次迭代就是上述的一次迭代过程,我们将弱分类器视作上述无参数模型\(F\)。弱分类器通常采用分类回归树,其复杂度会做适当限制以实现低方差的要求。GBDT最终通过加权求和的方式将多个弱分类器结合在一起实现总分类器,这就是GBDT中Boosting的由来。注意,Gradient Boosting对采用什么样的弱分类器来说是完全独立的,
分类回归树(CART):参考资料
每个弱分类器在逻辑上拟合的目标值是一个梯度,其可以被描述为:
其中\(L\)表示损失函数\(Loss(F(\bold x_i), y_i)\),\(F(\bold x)\)表示样本\(\bold x\)的预测值。\(i\)表示了不同迭代次数,\(F_i\)对应不同迭代阶段的弱分类器,注意这里求的梯度是将每个数据点\(\bold x_k\)处的函数值\(F(\bold x_k)\)视作该弱分类器的一个参数,然后计算损失函数对这种形式的“参数”的梯度。这种的方法好处在于利用函数在各个点的取值来描述一个无参数的模型。
这里存在两个问题,一是k明显是一个离散值,因此我们在取\(\bold x_k\)时实际需要进行离散化的考虑;二是我们如何用N个离散值\(F(\bold x_k)\ for\ k=1,2,3,...,N\)来计算出拟合函数\(g_i\),我们采用了决策树的方式来进行拟合,这也是GBDT中Decision Tree的由来。
人们常说GBDT利用了残差来进行迭代,但实际上使用的是否是残差取决于你的损失函数如何定义,只有在使用平方差损失函数时,对应的梯度才是残差。如果采用的是绝对差值损失函数,那么最终得到的梯度实际上是一个符号函数而不是残差。
而如果你问如何采用多个离散值来计算出弱分类器,这就其实是一个简单问题。假设你已知了k个样本的标记(即上述的k个离散值),那么建立一颗回归或者分类决策树是非常简单的。
最终经过m轮迭代,我们得到m个弱分类器,最终进行加权求和,权重与每轮残差有关。(你也可以直接相加,只是我觉得利用残差信息更合理一些)。