有一句话在业界广为流传:特征工程决定了模型的上界,调参决定模型能够有多逼近这个上界。
这里以sklearn为例讲讲特征工程。
一图概览特征工程
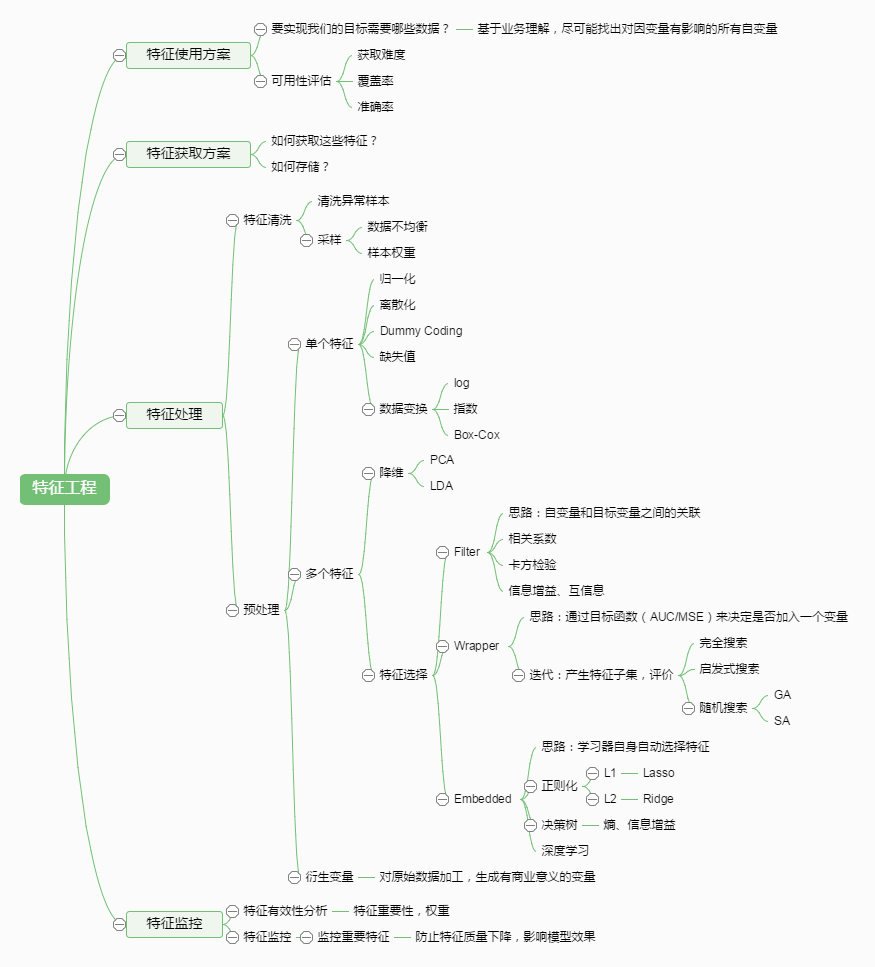
虽然说分了这么多部分,但特征工程最重要的部分还是特征处理,特征处理主要包含三个方面,特征预处理,特征选择和降维度。
数据预处理
数据预处理一方面把特征转为合适的编码喂给我们学习算法,另一方面就是把数据都转化到一个同一个规格。我们平时会用公制单位,那么对于特征也要转化到这样的公制单位。都是身高体重的数据,转化到公制下比较方便。
无量纲化
即把特征转化到“公制”。
标准化,使得特征均值为0。
from sklearn.preprocessing import StandardScaler。
[x = frac { x - overline { X } } { s }
]
归一化,使得特征为一个单位向量。
from sklearn.preprocessing import Normalizer。
[x ^ { prime } = frac { x } { sqrt { sum _ { j } ^ { m } x [ j ] ^ { 2} } }
]
特征编码
特征编码即将男女这样的特征进行编码,转化为01值。
二值化,设定一个阈值,大于等于阈值为一类,小于阈值为一类。
from sklearn.preprocessing import Binarizer。
one-hot编码,将多分类的特征变成一个特征向量。
from sklearn.preprocessing import OneHotEncoder。
特征选择
Filter
filter方法就是对特征进行评分,然后选择评分高的特征。那么既然是评分就要涉及到评分方法了。一般有四个评分方法。
- 方差
from sklearn.feature_selection import VarianceThreshold
- 相关系数
from sklearn.feature_selection import SelectKBest
- 卡方检验
from sklearn.feature_selection import SelectKBest
- 互信息
from sklearn.feature_selection import SelectKBest
详细翻阅参考。
降维
降维两种方法其实之前已经讲过了即PAC和LDA。
from sklearn.decomposition import PCA
#主成分分析法,返回降维后的数据
#参数n_components为主成分数目
PCA(n_components=2).fit_transform(iris.data)
from sklearn.lda import LDA
#线性判别分析法,返回降维后的数据
#参数n_components为降维后的维数
LDA(n_components=2).fit_transform(iris.data, iris.target)